Pendule
élastique, circuit RLC, interférences, concours d'entrée en première
année de cycle
ingénieurs filière sciences et technologie.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Pendule élastique. (5 points).
Un pendule élastique vertical est constitué d'un solide ponctuel S de
masse m = 300 g fixé à l'extrémité d'un ressort de masse négligeable et
de raideur k. Prendre g = 10 m s-2. Lorsqu'on accroche S sur
le ressort celui-ci s'allonge de x0 = 2,5 cm lorsque
l'ensemble solide ressoort est à l'équilibre.
1. Calculer la
raideur du ressort.
Poids P = mg ; force de rappel exercée par le ressort : F = kx0.
A l'équilibre : mg = k x0 ; k
= mg / x0 =0,300 x 10 / 0,025 =1,2 102 N / m.
2. L'ensemble étant à l'équilibre,
on étire S du point O de OA = a = 1 cm et on le lance vers le haut avec
une vitesse de module v0 = 0,78 m /s à la date t =0. S
oscille ensuite librement. Les forces dissipatives sont négligées.
L'origine de l'énergie potentielle de pesanteur est la position
d'équilibre du solide. L'abscisse de M est z = mesure algébrique de OM.
2.1 Faire le schéma et représenter
les forces appliquées au solide S à un instant quelconque.
2.2. Déterminer
l'équation différentielle du mouvement de S.
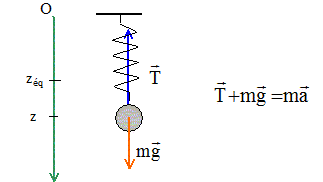
Ecrire la seconde loi de
Newton sur l'axe Oz : -k(z-L0)+mg=mz"
-k(z-zéq +zéq
-L0)+mg = mz" ; -k(z-zéq ) -k(zéq -L0)+mg
= mz"
Or k(zéq -L0)=
mg d'où : -k(z-zéq ) = mz".
On choisit la position
d'équilibre comme nouvelle origine en posant u = z-zéq :
il vient : -ku = mu" soit u"
+k/m u= 0 ; u"+w2u = 0 (1) avec w2 = k/m = 120 / 0,3 =400 ; w = 20 rad /s.
2.3. L'équation horaire du mouvement
est de la forme z = Zm sin ( wt+f). Déterminer Zm, w et f.
Zm n'est pas égal à "a" car le pendule est lancé initialement avec une vitesse v0.
On choisit un axe vertical orienté vers le haut, l'origine est à la position d'équilibre.
Vitesse dz/dt
= Zm w cos ( wt+f).
A t = 0 ; v0 =Zm
w cos (f)= 0,78.
Zm cos (f)= 0,78 / 20 = 0,039.
A t = 0, z = -a
: -a = Zm sin (f) ;
tan (f) =-a / 0,039 = -0,01 / 0,039 = -0,251 ; f
~ -0,25 rad.
Par suite Zm =-a / sin
(f) =-0,01 / sin(-0,25) ~
0,04026 m.
z = 0,04 sin (20 t-0,25).
2.4. Déterminer l'énergie mécanique
du système ressort solide S.
Energie mécanique = énergie potentielle élastique + énergie potentielle de pesanteur + énergie cinétique.
EM = ½kz2 + mgz + ½mv2 =½ka2 + ½mv02
en absence de forces dissipatives.
EM
=0,5 x120 x 0,012 +0,5
x0,30 x0,782 = 0,006 +0,09126 =0,09726 ~0,097 J.
2.5. A quelle date le solide S
passe-t-il pour la première fois par sa position d'équilibre ?
L'énergie
mécanique est sous forme cinétique à la position d'équilibre, cette
position étant prise comme origine des énergies potentielles.
La vitesse est alors maximale.
Au passage pour la première fois à la position d'équilibre, la vitesse est dans le sens de l'axe :
Donc cos (20 t-0,25) = 1.
20 t-0,25 = 0.
t = 0,251 / 20 ~ 0,013 s.
|
|
....
|
Circuit RLC. 4 points.
Un
circuit RLC série comprend un résistor R = 30 ohms, une bobine
d'inductance L = 0,30 H et un condensateur de capacité C = 20 µF. Ce
dipôle est alimenté par une tension sinusoïdale variable de pulxation w
variable de valeur efficace constante U = 100 V.
1. Déterminer à la résonance les valeurs de w0 et I0 de la pulsation et de l'intensité du courant.
A la résonance LC w02 = 1.
w0 = 1 /(LC)½ =1 / (0,30 x20 10-6) ½ ~ 408 rad /s.
I0 = U / R = 100 / 30 ~3,3 A.
2. Pour w1= 500 rad /s, déterminer le déphasage entre l'intensité et la tension.
La phase de l'intensité est prise comme origine des phases.
tan j = (Lw - 1 /(Cw)) / R.
tan j =(0,3 x400 -1 /(20 10-6x400)) / 30 =(120 -125) /30 =-0,167 ; f ~ -0,165 rad.
3. Exprimer I0 en fonction de I, w, w0 et Q ( facteur de qualité du dipôle, où I est l'intensité du courant correspondant à la pulsation w.
Q = Lw0 / R=1/ (RCw0).
Z =[R2 +(Lw-1/(Cw))2]½ =U / I.
U =[R2 +(Lw-1/(Cw))2]½ I
I0= U / R
RI0 =[R2 +(Lw-1/(Cw))2]½ I.
I0 =[1 +(Lw / R-1/(RCw))2]½ I.
I0 =[1 +(Qw / w0 - (Qw0/w))2]½ I.
Interférences.
On réalise des interférences à la surface de l'eau à partir de deux points sources S1 et S2 animés par un même vibreur.
Les sources vibrent à la même fréquence, avec la même amplitude et sont constamment en opposition de phase.
1. Ecrire l'équation d'un point M situé à une distance d1 de S1 et d2 de S2.
Signal émis par S1 : s1(t) =a cos (wt) ;
Signal émis par S2 : s2(t) =a cos (wt+p) .
En un point M : s1(M,t) =a cos (w(t-d1 /c)) = a cos(wt-wd1 /c).
s2(M,t) =a cos (w(t-d2 /c)+p))=a cos(wt-wd2 /c+p).
Le signal résultant est de la forme :
s(M,t) = s1(M,t) +s2(M,t).
cos p + cos q = 2 cos ((p+q)/2)cos ((p-q) / 2).
s(M,t) =2 cos (wt-w(d1+d2)/(2c)+p/2) cos(w(d2-d1) / (2c)+p/2).
Interférences constructives : w(d2-d1) / (2c)+p/2 = 2 kp avec k appartenant à Z.
w = 2p / T ; w / (2c) = 2p / (2cT) = p / l.
(d2-d1) / l = 2 k+1/2.
La différence de marche est égale à un nombre impair de demi-longueur d'onde.
Interférences destructives : w(d2-d1) / (2c)+p/2 = (2 k+1)p/2 avec k appartenant à Z.
(d2-d1) / l = 2 k.
La différence de marche est égale à un nombre entier de longueur d'onde.
|
|
