Mathématiques, Concours interne IIM 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Problème 1. L'objet est la construction d'approximations numériques de p. 1.1 Pour tout entier naturel n on note Sn la somme 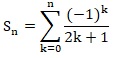 Montrer que pour tout k entier naturel l'intégrale suivante existe et la calculer. La fonction f(x) = x2k est continue car dérivable. L'intégrale converge sur l'intervalle [0 ; 1]. 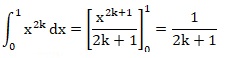1.2. 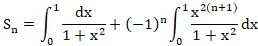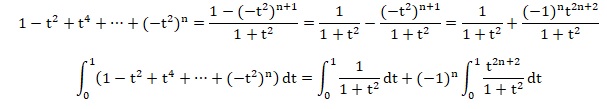Démontrer que pour tout n entier naturel, on a : 1.3. 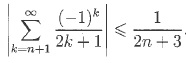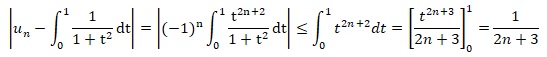En déduire que cette série est convergente, préciser sa somme et montrer que, pour tout n entier naturel : 1.4. Soit e > 0, combien de termes de la série 4 Sn est-il suffisant de calculer pour obtenir une approximation de p à e près ? Donner la valeur numérique pour e = 10-2. 4 un converge vers p. Il suffit de trouver n tel que 1 / (2n+1) < 0,01. 1 < 0,02 n +0,01. n > 0,99 / 0,02 ~50. 2. Formule de Machin. 2.1. Soient a et b deux réels tels que cos a, cos b et cos (a+b) soient non nuls. Exprimer tan (a+b) en fonction de tan a et  tan b. tan (a+b) = sin (a+b) / cos ( a+b). sin (a+b)=sin a cos b + cos a sin b. cos(a+b) = cos a cos b - sin a sin b. Or tan a = sin a / cos a soit sin a = tan a * cos a ; de même sin b = tan b * cos b. sin (a+b)=tan a * cos a * cos b + cos a * tan b * cos b = cos a *cos b ( tan a + tan b). cos(a+b) = cos a cos b -  tan a * cos a * tan b * cos b = cos a *cos b (1-tan a * tan b). tan (a+b) =( tan a + tan b) / (1-tan a * tan b). On pose t = tan x ; tan (2x) = 2t / (1-t2). 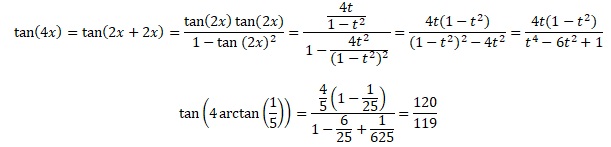2.2. On pose a = Arctan (1 /5) et b = Arctan (1 / 239). Calculer tan (4a-b) et en déduire la valeur de 4a-b. tan (a-b) = (tan a - tan b) / (1+tan a * tan b). 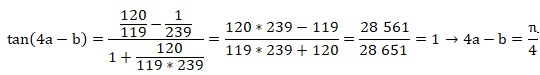tan ( 4 Arctan (1/5)-Arctan(1 / 239)) = [ tan( 4 Arctan (1/5) ) -tan (Arctan (1 / 239)) ] / [1+tan( 4 Arctan (1/5) )tan (Arctan (1 / 239)) ] 2.3. Rappeler le développement en série entière de 1 /(1+x) et préciser son rayon de convergence. En déduire celui de Arctan ainsi que son rayon de convergence. 1 / (1+x) = 1-x+x2 +... +(-1)n xn. un+1 / un = (-1)n+1 xn+1  /(-1)n xn) = -x. Quand  n tend vers plus l'infini, un+1 / un tend vers -x. Rayon de convergence R = 1 /x. Développement limité de Artan(x). On change de variable : 1 / (1+x2) = 1-x2+x4 +... +(-1)n x2n. On intègre car ( Arctan x )' = 1 / (1+x2). x-x3 / 3 +...+(-1)n x2n+1 / (2n+1). 2.4. En déduire une série numérique dont p est la somme. Que pensez de la vitesse de convergence de cette série par rapport à celle de la question 1 ? p = 4 (Arctan (1/5) -Artan(1/239). p = 4[4a-b]=4 [ 4(1 /5 -1/53 /3+...+(-1)n (1/5)2n+1 / (2n+1)-( 1 /239 -1/2393 /3+...+(-1)n (1/239)2n+1 / (2n+1))]. Cette série converge très rapidement. . . .... Problème 4. Un modèle d'évolution de populations animale relie le nombre d'individus y(t) en fonction du temps t à la variation y'(t) de ce nombre et aboutit à une équation différentielle non linéaire du type y'(t) = a y(t) -by(t) ½. (E). a et b sont deux réels positifs. On étudie ce problème pour t appartenant à R+. L'objet de ce problème est de résoudre l'équation (E) à l'aide d'un changement d'inconnue et de comprendre l'évolution finale de la population en fonction du nombre d'individus initial y(0) = y0 appartenant à R+. 1. A quelle condition portant sur y0, le nombre d'individus reste-t-il constant au cours du temps ? y'0 = 0 ; ay0-by0½ = 0 ; ay0½ -b = 0 ; y0 = (b / a)2. 2.  On suppose que y est une fonction strictement positive sur un intervalle I. 2.1. Montrer que y est solution de (E) si et seulement si la fonction z2 =y est solution strictement positive sur I d'une équation différentielle linéaire (E') que l'on précisera. y' = 2z z' ; 2z z' = az2-bz. 2z' = az -b  ; z'-0,5 az = -0,5 b (E'). 2.2. Résoudre (E') et préciser le signe de ses solutions. Solution générale de z' -0,5 az = 0. z=A e0,5at avec A une constante. Solution particulière de (E') : z = b / a. Solution générale de (E') : z=A e0,5at +b / a. 2.3. En déduire la forme générale des solutions de (E) avec leur intervalle de définition puis parmi ces solutions celle vérifiant y(0) = y0. y =z2 = (A e0,5at +b / a)2 =A2eat +(b/a)2 +2Ab / a e0,5at . y0 =A2 +(b/a)2 +2Ab / a = (b / a)2. A2 +2Ab / a = 0 ; A=-2b /a. y = (-2b /a e0,5at +b / a)2 . y = (b/a)2(1-2 e0,5at)2. y = y0(1-2 e0,5at)2. 3. Préciser, en fonction de y0, a et b, l'évolution de la population, au fil du temps. Indiquer lorsqu'il y a lieu le temps au bout duquel la population étudiée s'éteint. y0(1-2 e0,5at)2 = 0. 1-2 e0,5at = 0. e0,5at =0,5 ; 0,5at = ln(0,5) = -ln(2). t = -2 ln(2) /a ; impossible t est positif ( la population ne s'éteint pas).

menu