Physique,
Concours interne IIM 2021.
Instruments à cordes, optométrie
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
...
|
.
.
|
..
..
......
...
|
Instruments
à cordes.
On
considère une corde de masse linéique µ dans un repère orthonormé Oxy.
Au repos elle est rectiligne, parallèle à l'axe horizontal Ox et
tendue avec une tension T0.
En mouvement, le déplacement du point de la corde en x à l'instant t
est noté y(t). On suppose que les déplacements sont petits, de même que
l'angle a que
fait la corde avec l'axe Ox. On suppose aussi que le module de la
tension T est une légère perturbation par rapport à sa valeur au repos.
On néglige les effets de la pesanteur.

1) On considère
l'élément de corde dl situé entre les plans d'abscisses x et x+dx.
Montrer que dl ~dx.
cos a ~ 1 =dx /
dl ; dl ~dx.
2) et 3) Montrer que l'on peut écrire
pour un élément de masse dm la relation suivante.
dm = µdx.
Théorème du centre d'inertie appliqué à un
élément de corde situé entre las abscisses x et x+dx :
Au premier ordre T = T0.
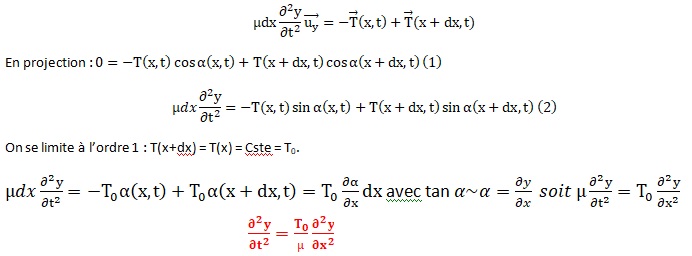
4) A quoi
correspond le paramètre c2 =T0 / µ ?
c =(T0 /µ)½ est la vitesse de propagation de
l'onde sur la corde exprimée en m / s.
5) On effectue le
changement de variable suivant : x = x+ct et h = x-ct.
En déduire la relation suivante.
t = (h
-x) / (2c) ; x = (h +x) / 2.
y peut être considérée comme une fonction de x et
h.
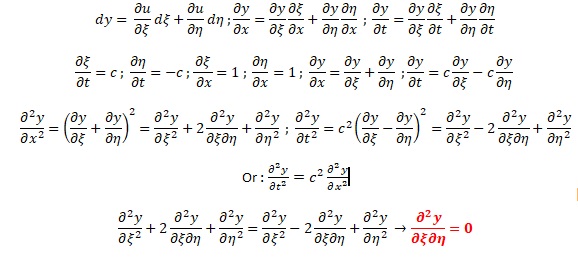
6) En déduire qu'il
existe des fonction f et g telles que y(x,t) = f(x+ct) +g(x-ct) et
donner le sens physique de ces fonctions.
La forme de l'onde observée à l'instant t, doit se retrouver à
l'instant t+t par
une translation d'ensemble des ces points constitutifs d'une distance ct.
f(t+t, x+ct) = f(t, x).
f doit donc dépendre uniquement de la combinaison x+ct.
Un raisonnement comparable pour les ondes se propageant vers les x
décroissants, conduit à :
g(t+t,
x-ct) =g(t, x).
g doit donc dépendre uniquement de la combinaison x-ct.
f(x+ct) décrit une onde se propageant vers
les x croissants et g(x-ct) décrit
une onde se propageant vers les x décroissants.
7. On
considère que la corde est fixée à 2 extrémités x=0 et x = L. Rappeler
de manière générale, le principe d'une onde stationnaire. En analyse,
comment appelle t-on ce type de problème posé par cette équation aux
dérivées partielles ?
Lorsqu'une onde rencontre
un obstacle rigide, elle produit une onde réfléchie
: la superposition d'une onde progressive
sinusoïdale de fréquence f et de l'onde réfléchie
sur un obstacle fixe produit une onde
stationnaire :
une vibration sans propagation, de fréquence f. ... L'onde subit
une réflexion sur chaque extrémité.
8. En posant y = f(x) . g(t),
montrer que les solutions en ondes stationnaires de l'équation obtenue
en 3) sont de la forme :
y(x,t) = y0 cos ( wt+f) cos(kx+F).
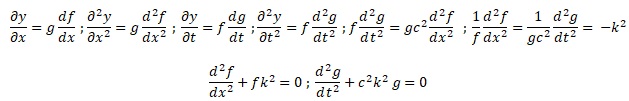
-k2 : constante de séparation.
f(x) = A cos ( kx+ f)
; A est une constante.
La corde est fixée en x=0 et en x= L :
f(0) = 0 = A cos ( f) ; f = ±p/2.
f(L) = 0 =
A cos ( kL+ f)
;
kL+ f = ±p/2
(2p) ; k =n p/ L.
f(L) = B cos
( ckt+ F) ; B est
une constante.
y = f(x) . g(t)= y0 cos ( wt+f) cos(kx+F).
wn =
ck =n c
p/ L.
9. Définir les
modes propres de la corde. Montrer que les fréquences propres sont de
la forme fn = nc / (2L)
La fréquence
propre d'un système est la fréquence à laquelle il oscille
librement ( sans force excitatrice extérieure et sans force
dissipative) .
Toute vibration de la
corde pour laquelle chaque point vibre de manière
sinusoïdale avec
la même fréquence est un mode propre de vibration.
fn =wn /(2p)= nc / (2L)
10. Proposer une expérience
permettant de mesurer les fréquences propres d'une corde vibrante.
On continue
par l'expérience de la corde de Melde. Cette corde est
supposée inextensible, de longueur L, de masse linéïque µ. Elle est
tendue à la tension T à l'aide d'une masse accrochée à la
corde via une poulie parfaite et excitée par un vibreur de mouvement
vertical a cos (wt)
à son autre extrémité.
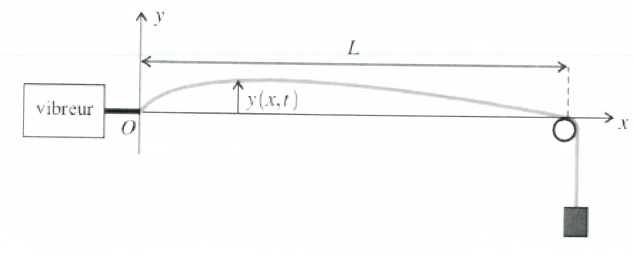
Dans l'expérience de la corde de Melde, la
fréquence du vibreur est
réglée à l'aide d'un GBF.
Faire varier la fréquence du GBF jusqu'à obtenir un seul fuseau ample
entre O et la poulie.
11. Donner la définition de la note
de fréquence fondamentale émise par la corde de l'instrument.
n = 1 : fréquence fondamentale ; n > 1 : harmoniques.
12. La gamme des
sons audibles par l'homme s'étend environ de 20 Hz à 20 kHz. En déduire
la nécessité d'avoir des cordes de carctéristiques différentes sur un
même instrument.
f =1/(2L)( F/µ)½ avec
L, µ constants
pour une corde donnée.
Pour augmenter la fréquence f, il faut augmenter la tension F de la
corde ou diminuer la masse linéïque µ.
La longueur de la corde, sa tension et sa masse linéïque étant
limitées, il faut nécessairement plusieurs cordes sur un même
instrument, pour couvrir la gamme de fréquences 20 Hz- 20 kHz.
|
|
....
|
Optométrie.
L'oeil
"réduit" est un modèle optique simple de l'oeil humain. L'oeil est
considéré comme rempli d'un milieu homogène d'indice n et le seul
élément réfractif pris en compte est la cornée de rayon de courbure R.
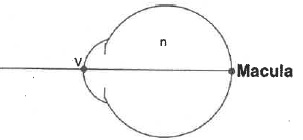
1.
On appelle punctum remotum PR le point conjugué avec la macula quand
l'oeil n'accommode pas et on note k la distance entre ce point et le
vertex de la cornée (V). On note k' la longueur axiale de l'oeil
( distance V-macula). On assimile la cornée à une lentille mince de
distance focale f ' placée en V. Rappeler l'équation de
conjugaison reliant k, k' et f '.
PR : point le plus éloigné que peut voir l'oeil de façon nette ( à l'infini pour un oeil emmétrope).
Relation de conjugaison des lentilles minces.
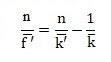
2. On appelle K = 1 / k l'erreur réfractive. Discuter du type de défaut de la vision en fonction du signe de K.
Myopie : vision nette des objets proches, mais pas celle des objets éloignés.
L'oeil est trop long ou trop puissant.
Hypermétropie : vision nette des objets éloignéss, mais pas celle des objets proches.
L'oeil est trop court ou pas assez puissant.
3. On considère un oeil d'indice n = 1,36 avec R = 5,58 mm et une longueur de 21,42 mm.
Sa puissance optique est F = (n-1) / R en dioptries. Calculer l'erreur réfractive en dioptries et commenter.
F = (1,36-1) / (5,58 10-3) =64,5 dioptries.
F = n / f ' ; f ' = n / F = 1,36 / 64,5 =0,02108 m = 21,08 mm.
L'image d'un objet à l'infini se forme devant la rétine. Cet oeil est trop long ( myopie ).
4.
On considère un oeil myope dont le PR est à 50 cm. On place devant cet
oeil, à une distance d de V une lentille mince L, divergente de focale
f". Pour un objet à l'infini (O), où se trouve l'image (O') de cet
objet par L ?
L'image d'un objet à l'infini se trouve dans le plan focal image de cette lentille.
5. On souhaite que
cette image O' se forme au punctum remotum PR. Représenter le système
optique et la formation de l'image de O' par L. En déduire une
relation liant f ", k et d. Où sera formée l'image de (O') par l'oeil ?
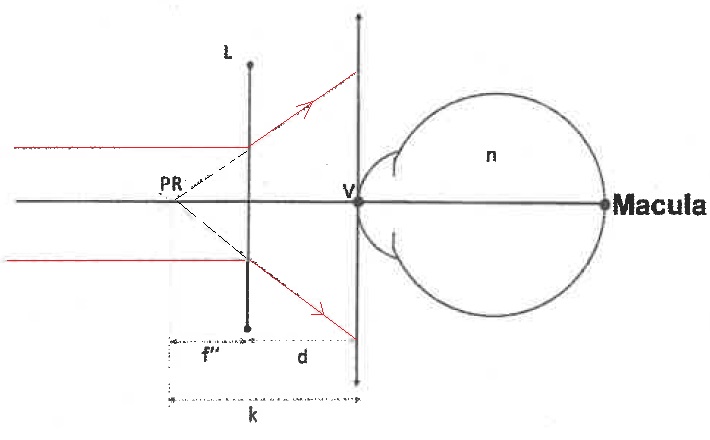
L'objet se trouvant à l'infini, l'image O' se forme dans le plan focal image de cette lentille L.
Pour une lentille divergente f " < 0 ;
L'objet étant situé à gauche de V, k < 0 ;
par suite : d = f "-k soit f " = d+k.
L'image définitive nette se trouve sur la rétine ( macula).
6. En notant FSL = 1 / f " montrer que FSL = K /(1+dK).
f " = d+k ; FSL=1 / f ''= 1 / (d+k) = 1 / (k(d / k+1) = K / (Kd+1).
7. Pour une erreur réfractive donnée, comparer la correction requise avec des lunettes ou des lentilles de contact.
Pour des lentilles de contact, d = 0 et FSL lent contact = K.
Pour des lunettes FSL lunettes = K / (Kd+1) inférieur à FSL lent contact .
8. Expliquer comment la diffraction peut limiter le pouvoir de résolution de l'oeil.
9. Quels sont les paramètres contrôlant cette diffraction ?
La diffraction au niveau de la pupille limite le pouvoir de résolution de l'oeil.
Le plus petit diamètre angulaire séparable est Dq = 2,44 l/D avec D diamètre de la pupille.
|
|