Math�matiques, �quation diff�rentielle, concours Geipi polytech 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts. .. .. . . .. .. ...... ... Exercice 3 (27 points). On souhaite �tudier l'�volution au cours du temps de la concentration d'un analg�sique dans le sang : par voie intraveineuse dans la partie A, puis par voie orale dans la partie B. A. Voie intraveineuse.   l est une constante r�elle strictement positive. On consid�re l'�quation diff�rentielle (E1) : y '(t) = -l y(t) o� y est une fonction d�finie pour tout r�el t. 1. D�terminer la solution g�n�rale de (E1). y = A e-lt avec A une constante. 2. On appelle Q la solution de (E1) v�rifiant Q(0) = 0,6. Donner l'expression de Q. Q(0) = A e0 = 0,6 ; A = 0,6. Q(t) =0,6 e-lt . 3. Donner la limite de Q en plus l'infini. Donner le sens de variation de Q. e-lt tend vers z�ro quand t tens vers plus l'infini. Q(t) est strictement d�croissante de 0,6 � 0. A l'instant t=0, une dose d'un analg�sique est inject� dans le sang par voie intraveineuse. La subsatnce se r�partit instantan�ment dans le sang, ce qui donne une concentration initiale de 0,6 mg / L et est ensuite progressivement �limin�e. Au bout d'une heure la concentration de m�dicament pr�sente dans le sang a diminu� de 30 %. 4. Calculer l. Q(1) =0,6 e-l =(1-0,3) x0,6 = 0,42 ; e-l =0,42 / 0,6 =0,7 ; l = -ln(0,7) ~0,3567 heure -1. Le m�dicament reste efficace tant que sa concentration reste sup�rieure � 0,1 mg / L. 5. D�terminer le temps d'efficacit� du m�dicament. Q(t) =0,6 e-lt > 0,1 ; e-lt > 1 /6 ; -lt > ln(1 /6) ; lt < ln(6) ; t < ln(6) / (-ln(0,7) ; t < 5,02 heures. B. Voie orale. On consid�re l'�quation diff�rentielle (E2) : y'(t) +y(t) = 0,5 e-0,5t. 6. V�rifier que g(t)=e-0,5t est solution de (E2). g'(t) = -0,5 e-0,5t. Repport dans (E2) : -0,5 e-0,5t+e-0,5t =0,5 e-0,5t est v�rifi�e quelque soit t. 7. Donner la solution f de (E2) v�rifiant f(0) = 0. Solution g�n�rale de y'(t) + y(t) = 0 : y(t) = A e-t avec A une constante. Solution g�n�rale de (E2) : y(t) = A e-t +e-0,5t . f(0) = 0 ; A e-0 +e-0,5 x0 =0 ; A+1 = 0 A = -1. f(t) = - e-t +e-0,5t . On consid�re la fonction q(t) = - e-t +e-0,5t . On note Cq sa courbe repr�sentative. 9. Donner la limite de q en plus l'infini. Les termes en exponentielle tendent vers z�ro et q(t) tend vers z�ro. 10. q' d�signe la fonction d�riv�e de q(t). q'(t) = e-0,5t(ae-0,5t +b). D�terminer a et b. q'(t) =e-t -0,5e-0,5t =e-0,5t(e-0,5t -0,5). a = 1 et b = -0,5. 11. Donner l'ensemble des solutions r�elles de l'in�quation q'(t) >0. e-0,5test toujours positif ; e-0,5t -0,5 > 0 ; e-0,5t >0,5. -0,5t > ln(0,5) ; -0,5t > -ln(2) ; t < 2 ln(2) ; t < ln(4). 12. Soit A le point de Cq d'abscisse xA = ln(4) et d'ordonn�e yA. Calculer yA. yA = - e-ln(4) +e-0,5ln(4) =- eln(1 / 4) +e0,5ln(1 /4) =-1 /4 +(1/4)�= -1 / 4 +1 /2 = 1/4. 13. Compl�ter le tableau de variation de q sur [0 ; +oo[. 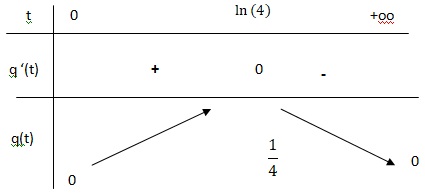Le m�dicament cause des effets ind�sirables quand sa concentration d�passe 0,3 mg / L. 14. Le m�dicament va t-il provoquer des effets ind�sirables ? Non, car la valeur maximale de q(t) est �gale � 0,25  < 0,3.   ... .... C. Comparaison des deux m�thodes. 15. QCM. Quel mode d'administration choisir pour �tre soulag� tout de suite de la douleur ? Voie orale ; voie intraveineuse ; n'importe lequel. 9. QCM. Sachant que l'analg�sique est efficace quand sa concentration dans le sang est sup�rieure � 0,1 mg / L par les deux m�thodes, quel mode d'administration choisir si on veut que le m�dicament soit efficace le plus longtemps possible ? Voie orale ; voie intraveineuse ; n'importe lequel. Par voie intraveineuse, le m�dicament est efficace durant 5 heures. 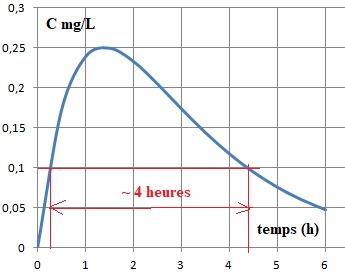Par voie orale : - e-t +e-0,5t > 0,1.

menu