Mathématiques,
géométrie, concours Geipi polytech 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1 (31 points).
A. Etude d'un triangle ABC.
On considère un triangle dont les sommets A, B et C sont définis
par leurs coordonnées : A(6,0) ; B(4 ; 8) C(-4 ; 0).
1et 2. Donner les coordonnées des vecteurs ainsi
que le produit scalaire suivants :
3. Donner la valeur exacte de la
norme de ces mêmes vecteurs.
4 et 5. Donner la valeur exacte de cos ß et sinß.
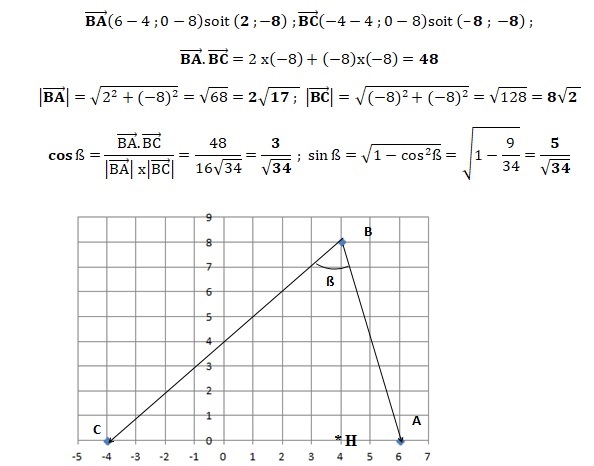
6. Montrer que l'aire du triangle ABC est 40
unités d'aire.
AC x BH / 2 =10 x 8
/ 2 = 40 unités d'aire.
B. Etude d'un tétraèdre ABCD.
Coordonnées des sommets : A(6 ; 0 ;
0) ; B(4 ; 8 ; 0 ); C(-4 ; 0 ; 0 ); D(-4 ; 0 ; 20).
Le triangle ABC est celui étudié dans la partie A, placé dans le plan
d'équation z = 0. La droite (DC) est parallèle à l'axe Oz.
7.
Que représente la droite (DC) pour le tétraèdre ABCD ?
La droite (DC) représente la hauteur issue du sommet D.
8. Calculer en unité de volume , le
volume de ce tétraèdre.
V = aire de base x hauteur / 3 = aire triangle ABC x CD / 3 =40 x 20 /
3 = 800 / 3 unités de volume.
9. 10 et 11. Donner une équation
cartésienne du plan (ABD).
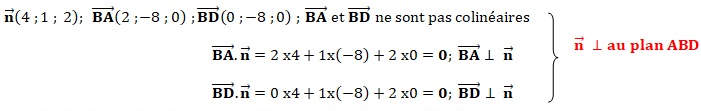 Equation cartésienne de
ce plan : 4x +y +2z +d = 0.
Equation cartésienne de
ce plan : 4x +y +2z +d = 0.
A appartient à ce plan : 4 xA +yA +2zA
+d = 0 soit d = -24.
4x +y +2z
-24 = 0.
12. On note A' le
point d'intersection du plan ( ABD) avec l'axe Oz. Donner les
coordonnées de ce point.
A' 0 ; 0 ; zA').
A' appartient au plan( ABD) : 4 xA' +yA'
+2zA' -24 = 0.
2zA'
-24 = 0 ; zA' = 12.
A' (0 ; 0 ; 12).
13. Déterminer le
réel k tel que :
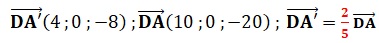
k = 2 / 5 = 0,4.
14. QCM. Soit (P)
le plan passant par A' parallèle au plan ( ABC). Soit ( A'B'C') la
section de (P) avec le tétraèdre ABCD. Quelle est la valeur approchée
en unité de volume, arrondie à l'unité, du volume du tétraèdre
A'B'C'D.A) 17 ; B) 107 ; C ; 160 ; D) 250.
Chaque longueur du tétraèdre ABCD est multipliée par 2/5=0,4.
Volume tétraèdre ABCD x0,43 = 800 / 3 x0,43 ~17.
|
...
|
....
|
C. Dans une sphère.
On appelle plan médiateur d'un segment non réduit à un point,
l'ensemble des points de l'espace équidistants des extrémités de ce
segment. c'est le plan perpendiculaire au segment en son milieu.
15. Déterminer les coordonnées I du
segment [AC].
xI = (xA+xC) / 2 =(6-4) / 2 = 1.
yI = (yA+yC) / 2 =(0-0) / 2 = 0.
zI = (zA+zC) / 2 =(0-0) / 2 = 0. I(1 ; 0; 0).
16. Donner les
coordonnées du vecteur suivant :
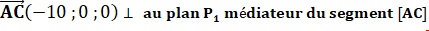
17. En déduire qu'une équation du
plan médiateur P1 du segment [AC] est x = 1.
P1 étant perpendiculaire en son milieu I du segment [AC] ,
l'équation de ce plan est :
-10 x +d = 0 ; I(1 ; 0 ; 0 ) appartient à ce plan : -10 +d = 0 soit d =
10.
-10x+10=0 soit x = 1.
18. Justifier
qu'une équation du plan médiateur P2 du segment [AB] est
x-4y +11 = 0.
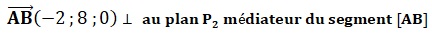
P2 étant perpendiculaire en son milieu J (5 ; 4 ; 0) du
segment [AB] , l'équation de ce plan est :
- 2x +8y+d = 0 ; J(5 ; 4 ; 0 ) appartient à ce plan : -10 +32+d = 0
soit d = -22.
-2x+8y-22=0 soit x -4y+11 =0.
On admet qu'une équation du plan médiateur P3 du segment
[CD] est z = 10.
19. En utilisant les équations des
plans médiateurs, déterminer les coordonnées du centre W de la sphère (S)
circonscrite au tétraèdre ABCD.
Le centre de la sphère est l'intersection des trois plans médiateurs.
xW
= 1 ; 1 -4yW+11
=0 soit yW=3
; zW=10
; W ( 1 ; 3 ; 10).
20. Calculer le rayon de cette
sphère.
WA
=[(6-1)2 +(0-3)2 +((0-10)2]½
=134½.
|
|