Mathématiques,
concours Puissance alpha 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1.
Un peu de lecture graphique.
On donne les points A(2 ; 4), N(0 ; 1), C(3 ; 10) et D(0 ; 8).
On considère la fonction f définie et dérivable sur R et représentée
par la courbe C et F une primitive de f représentée par la courbe en
pointillée G.
A est un point de la courbe C, B et C sont deux points de la courbe G.La droite (AD) représente
la tangente à C au point A.
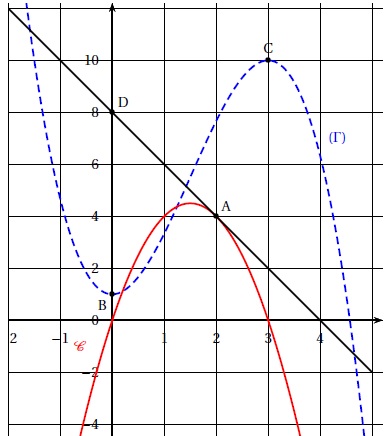
a. La fonction f '
est positive sur l'intervalle [0 ; 3]. Faux.
La fonction f est
croissante sur [0 ; 1,5] ; f ' est positive sur cet intervalle.
La fonction f est décroissante sur [1,5 ;
3] ; f ' est négative sur cet intervalle.
b. f '(2) = -3. Faux.
Coeficient directeur de
la droite (AD), tangente en A à la courbe C : f '(2)= -8 /4 = -2.
c. Le coefficient directeur de la
tangente à G au point
d'abscisse x=2 est égal à 4. Vrai.
f(2)=4.
d. 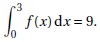 Vrai. Vrai.
F(3)-F(0)=10-1=9.
Exercice 2. Quelques
questions de logique.
Soit a et b deux nombres rééels tels que a < b et f, g h trois
fonctions définies sur un même intervalle I = [a ; b ].
a.Si,
pour tout nombre réel x de l'intervalle I, f(x) < g(x) <
h(x) et si les fonctions f et h admettent toutes les deux une limite
finie lorsque x tend vers a, alors la fonction g admet aussi une limite
finie lorsque x tend vers a. Faux.
b. Si, pour tout nombre
réel x de l'intervalle I, f(x) < g(x) et s'il existe deux nombres
réels L et L' tels que :
L= limite de f(x) quand x tend vers a et L' = limite de
g(x) quand x tend vers a.
Aloes L < L'. Vrai.
c. Si la fonction f
est continue en x = a, alors la fonction f est dérivable en x = a. Faux.
d. La réciproque
de c est fausse. Faux.
Exercice 3. Un peu de
géométrie avec le nombre d'or.
Soit
a un nombre réel strictement positif. Dans un repère orthonormé, on
pose B le point de coordonnées (a ; 0), C le point de coordonnées (a ;
a) et I le milieu du segment [OB]. On construit le quatrième sommet D
du carré OBCD, M le point de la demi droite [OB) tel que IM = IC et N
le quatrième sommet du rectangle OMND. On pose F l'abscisse du point M.
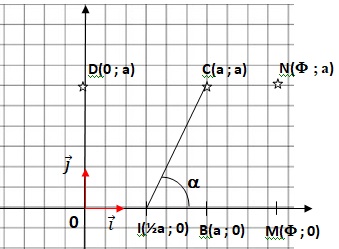
On appelle nombre d'or j,
l'unique solution positive de l'équation x2-x-1 = 0. Un
rectangle est dit d'or si le rapport entre la longueur L et la largeur l est L / l = j.
a. Si
a=1, alors F= j. Vrai.
j = (1+5½)
/ 2.
IC =(0,52
+12)½ =1,25½
; IM =F-0,5
=1,25½
; F = 0,5 +1,25½
=(1+5½)
/ 2.
b. Si a = 1, alors F = 1-1 / F. Faux.
1-1/ F =1-2/ (1+5½) =1-2(1-5½)/(-4) =1+(1-5½)/ 2.
c. OMND est un rectangle d'or. Vrai.
L=OM
=
F. OD = a
; L / l = F / a ;
IM = F-½a ; IC =(a2
+0,25a2)½ =1,25½a.
IM = IC ; F-½a = 1,25½a ; F = 1,25½a +½a ; F
/ a = ½+1,25½ =(1+5½)/ 2 = j.
d. cos a = (1+5½) / 4.
Faux.
cos a =IB / IC
=IB / IM=0,5 a /( F
-½a).
F -½a= a j -½a =a(j-½)= a[ (1+5½)
-1] / 2=5½a / 2.
cos a
= a / (5½a)=1
/5½.
Exercice 4. Un peu de lecture graphique.
Soit f la fonction définie par f(x) = x2-2 de courbe représentative Cf et b0 =3.
On définit pour tout entier n la suite (vn) par vn+1 = (v2n+2) / (2vn) et v0 = 3.
On pose B0 le point de coordonnées (b0 ; 0) et A0 le point de Cf d'abscisse b0.
A1 est le point de Cf d'abscisse b1, et B2 le point d'intersection de la tangente à Cf au point A1 avec l'axe des abscisses.
On recommence le même raisonnement et on pose, pour tout entier n, bn l'abscisse du point Bn.
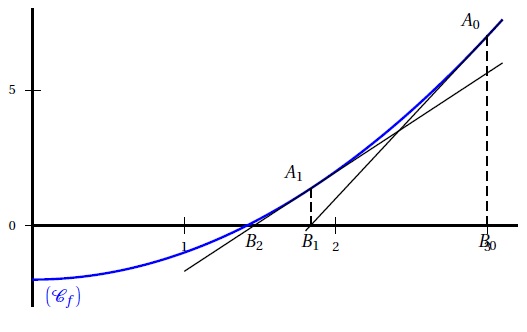
a. Pour tout entier réel a, la tangente à la courbe Cf au point d'abscisse a a pour équation y = 2ax+a2-2. Faux.
Coefficient directeur de la tangente à la courbe Cf : f ' (a) =2a-2.
Le point de coordonnées ( a ; f(a)=a2-2) appartient à la tangente.
Equation de la tangente : y = (2a-2)x +b.
a2-2 =(2a-2)a +b ; b = -a2+2a-2.
y = (2a-2)x -a2+2a-2.
b. b1 = 11 / 6. Vrai.
b1 = (b20+2) / (2b0) = (32+2) / (2*3) = 11 / 6.
c. Pour tout entier naturel n, bn+1 = b2n-2. Faux.
bn+1 = (b2n+2) / (2bn).
d. Soit N un entier naturel non nul. Les algorithmes suivants permettent de calculer le N-ième terme de la suite (vn). Vrai.

Exercice 5. Probabilités conditionnelles.
La probabilité que l'élève réponde correctement à la première affirmation est égale à 0,8.
Si l'élève répondait correctement à une affirmation il avait 9 chances
sur 10 de répondre correctement à la suivante. En revanche, si l'élève
se trompait sur une affirmation, il avait 7 chances sur 10 de
continuer à se tromper.
i est un entier naturel compris entre 1 et 4 et Ci est l'évenement " l'élève répond correctement à l'affirmation n° i".
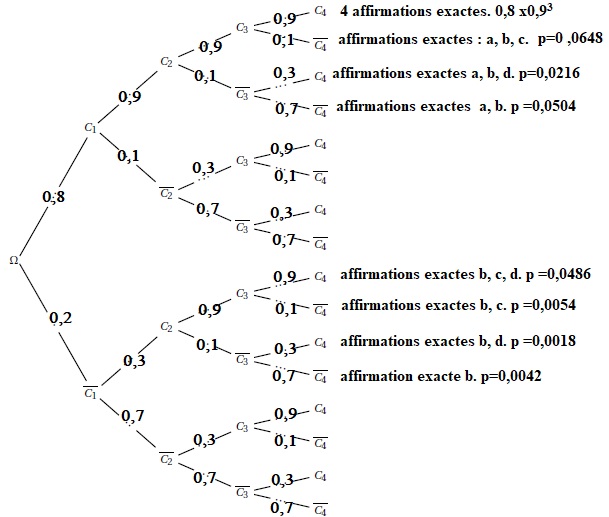
a. La probabilité de répondre correctement aux 4 affirmations est égale à p = 0,8 x0,94. Faux.
b. La probabilité de répondre à l'affirmation b est égale à p' =0,78. Vrai.
c.
La probabilité de répondre correctement à l'affirmation a sachant qu'on
a répondu correctement à l'affirmation b est égale à p" = 0,9. Faux.
p"= p(a n b) / p'=0,8 x0,9 / 0,78 =0,923.
d. La probabilité de répondre correctement aux affirmations b, c et d est égale à 0,93.
Faux
Exercice 6. Calcul d'intégrales.
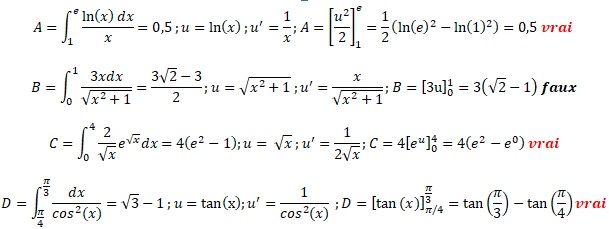
|
|
|
....
|
Exercice
7. Calculs de limites.
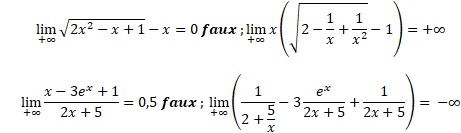
Soit (un) la suite définie par u0 =1 et pour tout entier naturel n, un+1=0,75 un.
Pour tout entier naturel n, on définit la suite (Sn) par Sn = u0 +u1 +u2 +...+un.
c. La suite (un) diverge. Faux.
u1=0,75 ; u2 =0,752; un = 0,75n.
d. La limite de Sn en plus l'infini est plus l'infini. Faux.
Somme des termes d'une suite géométrique de raison 0,75 et de premier terme 1.
Sn =(1-0,75n)/(1-0,75) =4
Exercice 8. Petite étude de fonction exponentielle.
Soit f la fonction définie sur R par f(x) =exp((x-1) / x2) de courbe représentative Cf et D la droite d'équation y=1.
a. f '(x) = (2-x) / x3 exp((x-1) / x2). Vrai.
On pose A = (x-1) / x2 ; on pose u = x-1 ; v = x2 ; u'=1 ; v' = 2x.
A' = (u'v-v'u) / v2 =(x2-2x2+2x)/x4=(-2x+2)/x3.
f '(x)= A' exp(A) = (2-x) / x3 exp((x-1) / x2).
b. Cf admet la droite D comme asymptote horizontale en +oo et en -oo. Vrai.
(x-1)/x2=1 /x-1/x2 tend vers zéro quand x tend vers ± oo.
c. Cf admet l'axe des ordonnées comme asymptote verticale. Faux.
La droite D est horizontale.
d. L'équation f(x) = 0 admet deux solutions sur R. Faux.
exp((x-1) / x2)=0, seule solution x = 0.
Exercice 9. Petite étude de fonction ln.
Soit f la fonction définie sut I =]1 : +oo[par f(x) = ln(x+1) / ln(x) de courbe représentative Cf.
a. Pour tout nombre réel x de I, f(x) = ln ((x+1) / x). Faux.
ln((x+1) / x) = ln(x+1) - ln(x).
b. f '(x) = [x ln(x/(x+1))-ln(x+1)] / [x(x+1)(ln(x)2].
Vrai.
On pose u = ln(x+1) et v = ln(x) ; u' = 1 /(x+1) ; v' = 1 /x.
(u'v-v'u) / v2 =[(ln(x) / (x+1) -ln(x+1) / (x ] / (ln(x))2.
[x ln(x)-(x+1)ln(x+1)] /[(x (x+1)(ln(x))2].
c. f est strictement croissante sur I. Faux.
f '(x) est du signe de x ln(x)-(x+1)ln(x+1).
(x+1)ln(x+1) > xln(x) sur I.
f '(x) < 0 sur I. f(x) strictement décroissante.
d. Cf admet la droite d'équation y = 0 comme asymptote horizontale en +oo. Faux.
Cf admet la droite d'équation y = 1 comme asymptote horizontale en +oo.
ln[x(1+1/x) / ln(x) est équivalent à ln(x) / ln(x) = 1 en plus l'infini.
Exercice 10. Petite étude de suite.
Soit la fonction f définie sur I =]0 : +oo[ par f(x)=0,25(x2-1) -2 ln(x) et F la fonction définie sur J =[e-1/8 ; +oo [ par F(x) = (1+8ln(x))½.
On pose (un) la suite définie par u0 =3 et un+1 = F(un).
On donne ln(2) ~0,7, ln(3)~1,1 et ln(4) ~1,4.
a. La limite de f(x) en plus l'infini est moins l'infini. Faux.
f(x)=0,25x2(1-1/x2-2 ln(x) / x2)
Par croissance comparée f(x) tend vers plus l'infini quand s tend vers plus l'infini.
b. L'équation f(x) = 0 admet deux solutions dont l'une x0 appartient à l'intervalle [3 ; 4]. Vrai.
f(3)~2-2*1,1 ~ -0,2 ; f(4)~3,75 -2*1,4 ~0,95.
f '(x)=0,5 x -2/x=(0,5 x2 -1) / x.
f '(x) positive sur ]2½ ; + oo[ et f(x) strictement croissante sur cet intervalle. L'une des solutions de l'équation f(x) = 0 appartient à [3 ; 4 ].
f '(x) négative sur ]0 ; 2½ [ et f(x) strictement décroissante sur cet intervalle.
f(x) tend vers plus l'infini quand x tend vers zéro.
f(2½)=0,25-ln(2) ~ -0,45. Il existe une autre solution à f(x) = 0 comprise ]0 ; 2½[.
c. x0 = F(x0). Vrai.
0,25(x02-1) =2 ln(x0) ; x02=1+ 8 ln(x0) ; (1+ 8 ln(x0))½=x0.
d. Pour tout entier naturel n, on a un > 3. Vrai.
ln(x) est strictement croissante ; donc 1+ln(x) est strictement croissante.
F(3) = (1+8ln(3))½~(1+8*1,1)½~9,9½ > 3.
Exercice 11. Notions de base sur les complexes.
a. (-3½+i)3 =8i. Vrai.
Module de z = -3½+i : |z| =(3+1)½ = 2 ; z / |z| = -3½ / 2 +i /2 =cos ( 5 p / 6) + i sin (5 p /6) = exp(i 5 p /6).
z = 2 exp(i 5 p /6) ; z3=23 exp(i 5 p /2)=8 exp(i p/2)= 8i.
b. La forme exponentielle de -3½ -i est -2 exp(i p /6). Faux.
Module de z = -3½-i : |z| =(3+1)½ = 2 ; z / |z| = -3½ / 2 -i / 2 =cos ( -5 p / 6) + i sin (-5 p /6) = exp(-i 5 p /6).
z = 2 exp(-i 5 p /6).
Soit f la transformation complexe du plan qui, à tout point M d'affixe différente de 3i associe le point M' d'affixe 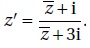
c. L'équation |z'| = 1 admet une unique solution dans C. Faux.
z = a+ ib ; z' = (a-ib+i) / (a-ib+3i)= (a+i(1-b) / (a+i(3-b).
|z' |=|a+i(1-b)| / |a+i(3-b)| =[a2+(1-b)2 ]½ / [a2+(3-b)2 ]½.
Si |z'| = 1 : a2+(1-b)2 =a2+(3-b)2 .
(1-b)2 =(3-b)2 ; 1-b =3-b ; impossible.
d. L'équation z' = 2 admet une unique solution dans C. Vrai.
a-ib+i =2(a-ib+3i)=2a-2ib+6i.
a-ib+5i=0 ; a+i(5-b)=0. a=0 ; b=5.
Exercice 12. Utilisation des nombres complexes en géométrie.
A, B, C et D sont les points du plan complexe d'affixes respectives zA = 3½i, zB =-3½i, zC=3+2i 3½ et zD = 3-2i 3½.
Le point E, d'affixe zE est le symétrique de D par rapport à O.
a. zE = -3 -2i 3½. Faux.
zE = -3 +2i 3½.
b. L'ensemble des points M du plan complexe tels que |z| =z est une droite. Faux.
z = x+iy ; |z| = (x2+y2)½ ;
si |z| = z :( x2+y2)½= x+iy soit y =0.
c. Les points A, B, C et D sont sur un même cercle de centre W d'affixe 3. Vrai.
WA2=9+3=12 ; WB2= 9+3=12 ;WC2= 0+4*3=12 ; WD2= 0+4*3=12.
d. 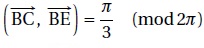 . Vrai. . Vrai.
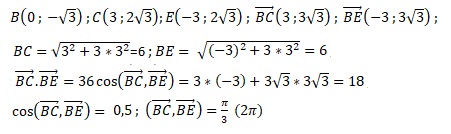
|
Exercice 13. Section dans un cube.
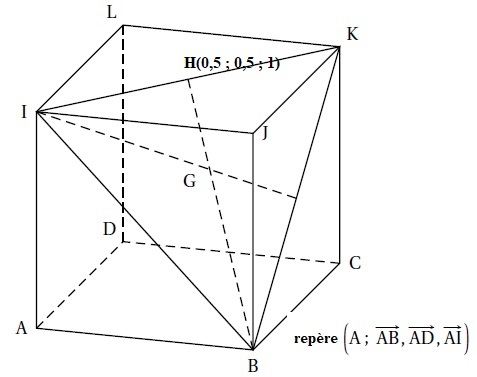
a. Le point G a pour coordonnées (-2 / 3 ; 1 / 3 ; 2 / 3). Faux.
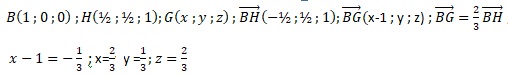
b. Les points J, G et D sont alignés. Vrai.
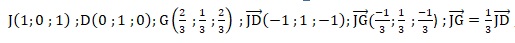
c. La droite (JD) et le plan (BIK) sont perpendiculaires. Vrai.
Equation du plan (BIK) : ax +by +cz+d=0.
B(1; 0;0 ) appartient à ce plan : a+d=0 ;
I(0 ;0 ;1) appartient à ce plan : c+d=0, d'où c = a.
K(1 ; 1 ; 1) appartient à ce plan : a+b+c+d=0 ; d'où b= -a ;
ax-ay+az-a=0 d'où l'équation de ce plan -x+y-z+1=0.
Coordonnées d'un vecteur perpendiculaire à ce plan : (-1 ; 1 ; -1).
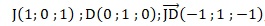
d. Le volume du tétraèdre IKBJ est égal à 1 /6. Vrai.
Aire du triangle IBK fois la hauteur JG / 3.
Aire du triangle IBK: BH x IK / 2.
BH= (0,52 +0,52 +1)½ =1,5½; IK =2½ : BH x IK / 2=3½ / 2.
JG=(1/32+1/32+1/32)½ =1/3½.
Volume du tétraèdre : 3½ / 2 x1 / 3½/ 3 = 1 /6.
Exercice 14. Probabilités continues.
Soit l un réel strictement positif. On pose a et ß deux nombres réels tels que 0 < a < ß < 1.
U la variable aléatoire suivant la loi uniforme sur l'intervalle [0 ; 1 ].
X la variable aléatoire définie par X = -1 / l ln(1-U).
a. Pour tout réel a de ]0 ; 1 [, P(U=a) >0. Faux.
b. Pour tout nombre réel a strictement positif, p(X< a)= p(U < 1-e-la). Vrai.
c. P(U < ß) = ß. Vrai.
d. P(a < X < ß)=e-lß-e-la. Faux.
Exercice 15. Suite de points.
Soit n un entier naturel non nul et (Mn) la suite de points de coordonnées (n ; 0).
Pour tout entier naturel n non nul, on pose An l'aire de la partie du plan comprise entre les demi-cercles de diamètres [OMn] et [OMn+1] et l'axe des abscisses.
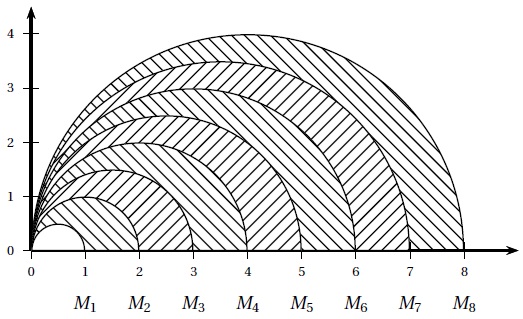
a. A1=3p ; A2=5p. Faux.
A1 = 0,5(p*12-p*0,52) =0,375p =3p / 8; A2 = 0,5(p*1,52-p*12) =0,625p= 5 p /8 =3p/8+p/4.
A3 = 0,5(p*22-p*1,52) =0,625p= 7 p /8 =5p/8+p/4.
b. An=2np+ p. Faux.
c. La suite (An) n >1 est une suite arithmétique de raison r = 2p. Faux.
d. Pout tout entier naturel n non nul, Sn = A1 +A2 +...+An=p/8 n(n+2). Vrai.
(An) n >1 est une suite arithmétique de raison r = p/4.
|
|