Oral
mathématiques,
concours Advance 2021.
Limites, logarithme exponentielle.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Limites.
21. Déterminer les limites suivantes quand x tend vers plus l'infini.
(2x2-5x) / (3x2+x+4). Forme indéterminée +oo / +oo.
Mettre x2, terme prépondérant, en facteur commun au numérateur et au dénominateur :
(x2 (2-5 /x)] / [x2(3+1/x-4/x2)]
Simplifier : (2-5 /x) / (3+1/x-4/x2).
Quand x tend vers plus l'infini : 5 /x, 1/x et -4/x2 tendent vers zéro.
La limite en plus l'infini de (2x2-5x) / (3x2+x+4). est donc 2 /3.
e2x / x= 2 e2x / (2x). Forme indéterminée +oo / +oo.
En plus l'infini, par croissance comparée, e2x / (2x) tend vers plus l'infini.
(ex+2x+2) / (x+3).
Mise en facteur commun du terme prépondérant : ex(1+2x / ex+2/ex) / [x(1+3 /x)].
ex / x (1+2x / ex+2/ex) / (1+3 /x).
En plus l'infini, par croissance comparée, 2x / exet 2/ex tendent vers zéro.
3 / x tend également vers zéro.
L'expression tend donc vers ex /x.
En plus l'infini, ex /x, par croissance omparée, tend vers plus l'infini.
22. Déterminer les limites suivantes en plus l'infini :
ln(x) / x2 = ½ln(x2) / x2. Forme indéterminée +oo / +oo.
Par croissance comparée, en plus l'infini, ln(x2) / x2 tend vers zéro.
(x2+ln(x)) / (3x2-x+2). Forme indéterminée +oo / +oo.
Mettre en facteur commun le terme prépondérant :
x2(1+ln(x) / x2) / [x2(3-1/x+2/x2)].
Simplifier : (1+ln(x) / x2) / (3-1/x+2/x2).
Par croissance comparée, en plus l'infini, ln(x) / x2) tend vers zéro.
De plus, 1/x+2/x2 tendent vers zéro.
La limite, en plus l'infini, de (x2+ln(x)) / (3x2-x+2) est donc 1 /3.
23. Déterminer les limites suivantes :
En zéro, limite de sin(x) / (2x) =½ sin(x) / x.
En zéro, la limite de sin(x) /x est égale à 1.
La limite cherchée est donc ½.
En plus l'infini, limite de x cos (1 /x).
En plus l'infini ; 1 /x tend vers zéro et cos(1/x) tend vers 1.
Par suite la limite en plus l'infini de x cos(1/x) est plus l'infini.
24. Calculer les limites suivantes en plus l'infini.
(x2-3)½-(x2+4x)½. Forme indéterminée +oo -oo.
Multiplier par l'expression conjuguée (x2-3)½+(x2+4x)½.
[(x2-3)½-(x2+4x)½] [(x2-3)½+(x2+4x)½] / [(x2-3)½+(x2+4x)½].
[(x2-3) -(x2+4x)] / [(x2-3)½+(x2+4x)½].
(-3-4x) / [(x2-3)½+(x2+4x)½].
Mise en facteur commun :
x(-3 /x-4) / [x(1-3/x2)½ +x(1+4/x2)½].
Simplifier : (-3 /x-4) / [(1-3/x2)½ +(1+4/x)½].
3 / x, 3/x2 et 4 /x2 tend vers zéro.
(-3 /x-4) / [(1-3/x2)½ +(1+4/x)½] tend vers-4 / 2 = -2.
sin(x) / (x2+3).
-1 < sin(x) < 1.
-1 /(x2+3) < sin(x) / (x2+3) < 1 /(x2+3)
En plus l'infini, 1 /(x2+3) tend vers zéro.
D'après le théorème d'encadrement des gendarmes sin(x) / (x2+3) tend vers zéro en plus l'infini.
25. Déterminer les limites suivantes :
(2-2x+3x2) / (4+x+6x2) en plus l'infini. Forme indéterminée oo /oo.
Mettre en facteur commun le terme prépondérant.
x2(2/x2-2/x+3) / [x2(4/x2+1/x+6)]
Simplifier :(2/x2-2/x+3) / (4/x2+1/x+6).
2/x2, 2/x, 4/x2et 1/x tendent vers zéro.
L'expression tend vers 3 /6 = 0,5.
En zéro, limite de sin(3x) / (2x). Forme indéterminée 0 /0.
3 sin(3x) / (6x)= 3 /2 sin(3x) / (3x).
On pose X = 3x : 1,5 sin(X) / X.
Or sin(X) / X tend vers 1 quand X tend vers zéro.
La limite de l'expression est donc 1,5.
|
|
....
|
Logarithme- exponentielle.
26. Résoudre dans R l'équation suivante :
ln(1-2x) = ln(x+2) + ln(3).
1-2x >0 soit x < 0,5 ;
ln(x+2) >0 soit x >-2.
Donc x appartient à ]-2 ; 05[.
ln(1-2x) = ln(3(x+2)) ;
La fonction exponentielle étant croissante sur R : 1-2x = 3(x+2) ; x =-1.
27. Résoudre dans R l'équation suivante : ln(2-x) < ln(2x+1)-ln(3).
2-x > 0 soit x < 2 ; 2x+1 >0 soit x > -0,5.
Donc x appartient à ]-0,5 ; 2 [.
ln(2-x) +ln(3) < ln(2x+1).
La fonction exponentielle étant croissante sur R : 3(2-x) < 2x+1 ; x > 1.
Solutions [1 ; 2 [.
28. Soit f la fonction définie sur R par ; f(x) = ex(2x-3).
a. Déterminer les limites de f en +oo et en -oo.
Quand x tend vers +oo : ex et (2x-3) tendent vers plus l'infini ; f(x) tend vers +oo.
Quand x tend vers -oo, ex tend vers zéro et 2x-3 tend vers -oo ; f(x) tend vers zéro.
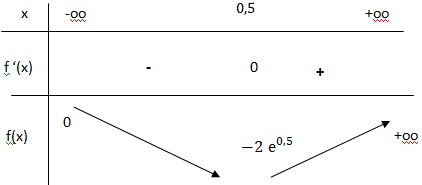
b. Dresser le tableau de variation de f sur R.
Calcul de f '(x) en posant u =ex et v = 2x-3 ; u' = ex ; v' = 2.
u'v+v'u = (2x-3)ex +2ex =ex(2x-1).
ex > 0, f '(x) a le signe de 2x-1.
x >0,5 ; f '(x) >0 et f(x) est strictement croissante.
x < 0,5 f '(x) < 0 et f(x) est strictement décroissante.
x = 0,5, f '(x )=0 et f(x) présente un minimum.
29. Résoudre dans R l'équation : ex-2e-x-1=0.
On pose X = ex > 0.
X-2/ X-1=0 ; ( X2-X-2) / X=0.
Discriminant D =(-1)2 -4(-2)=9=32.
Solution retenue :X = (1+3)/2 = 2.
x= ln(2).
30. Soit f la fonction définie sur R par : f(x) = 2ex+e-x+x.
a. Déterminer les limites de f en +oo et en -oo.
En plus l'infini : ex et x tendent vers +oo ; e-x tend vers zéro ; f(x) tend vers + oo.
En moins l'infini : ex tend vers zéro ; e-x tend vers +oo ; x tend vers -oo ;
e-x+x = e(-x) (1+x/e-x) : par croissante comparée x/e-x tend vers zéro et f(x) tend vers +oo.
b. Montrer que f '(x) = (ex+1)(2ex-1) / ex.
f '(x) = 2ex-e-x+1= (2e2x-1+ex)/ex.
Or (ex+1)(2ex-1) =2e2x-ex+2ex-1=2e2x+ex-1
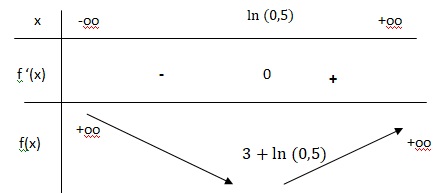
c. Dresser le tableau de variation de f(x) sur R.
ex >0 ; (ex+1) >0.
Le signe de f '(x) est celui de (2ex-1).
Si x > ln(0,5), f '(x) >0 et f(x) est strictement croissante.
Si x < ln(0,5), f '(x) <0 et f(x) est strictement décroissante.
Si x = ln(0,5), f'(x) = 0 et f(x) présente un minimum.
31. Soit f(x) définie sur R*+ par : f(x) = (2 ln(x)-1) / x.
a. Résoudre f(x) = 0.
2 ln(x)-1=0 ; ln(x) = 0,5 ; x = e0,5.
b. Résoudre f(x) > 0.
2 ln(x)-1 >0 ; ln(x) > 0,5 ;
La fonction exponentielle étant croissante sur R*+ : x > e0,5.
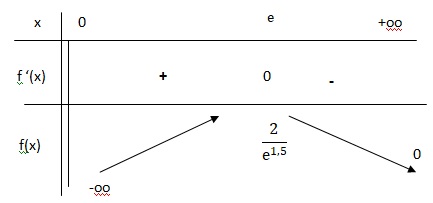
c. Dresser le tableau de variation de f(x).
Calcul de f '(x) en posant : u = 2ln(x)-1 et v = x ;u' =2 /x ; v' = 1.
(u'v-v'u) / v2=(2-2ln(x)+1 / x2 = 3-2ln(x) / x2.
Si x > e1,5, f '(x) < 0 et f(x) est strictement décroissante.
Si x appartient à ]0 ; e[, f ' (x) >0 et f(x) est strictement croissante.
Si x = e1,5, f '(x) =0 et f(x) présente un maximum.
32. Soit f(x) définie sur R*+ par : f(x) = x+1+ln(x) / x.
a. Déterminer les limites en zéro et en + oo.
En plus l'infini : ln(x) / x tend vers zéro par croissance comparée et f(x) tend vers +oo.
En zéro : ln(x) / x tend vers -oo et f(x) tend vers -oo.
b. Déterminer f '(x) puis le tableau de variation de f(x).
On pose u = ln(x) et v = x ; u' = 1/x et v' = 1.
(u'v-v'u) / v2 =(1-ln(x)) / x2.
f '(x) = 1+(1-ln(x)) / x2 = (x2-ln(x)+1)/x2.
On cherche le signe de g(x) =x2-ln(x)+1.
g'(x) = 2x-1/x = (2x2-1) /x.
x appartient à R*+ : x >0 et g'(x) = 0 si x = 0,5½.
g'(x) positive si x >0,5½ et g(x) est strictement croissante.
g'(x) < 0 si x appartient à ]0 ; 0,5½[ et g(x) est strictement décroissante.
Ordonnée du minimum g(0,5½) =0,5 -ln(0,5½) +1=1,5 +0,5ln(2) > 0.
Donc g(x) est toujours positive.
f '(x) >0 et f(x) est strictement croissante.
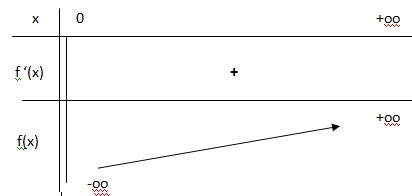
c. Déterminer une primitive de f(x).
On pose u = ln(x) ; u' = 1 / x ; ln(x) / x = u u'.
Primitive de ln(x) / x : ½ (ln(x))2.
Primitive de f(x) : F(x) =½x2 +x +½ (ln(x))2.
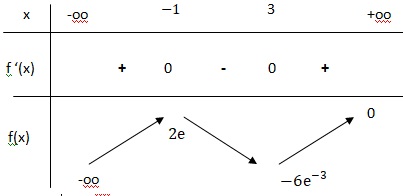
33. Soit f la fonction définie sur R par f(x) = (3-x2)e-x.
a. Déterminer les limites de f(x) en plus l'infini et en moins l'infini.
En plus l'infini e-x tend vers zéro et f(x) tend vers zéro.
En moins l'infini : e-x tend vers plus l'infini et - x2 tend vers moins l'infini : f(x) tend vers moins l'infini
b. Déterminer f '(x) puis le tableau de variation de f(x).
On pose u = 3-x2 et v = e-x.
u' = -2x ; v' = -e-x.
u'v+v'u = -2xe-x-(3-x2)e-x=e-x(x2-2x-3).
e-x >0 ; f '(x) a le signe de x2-2x-3.
x2-2x-3 = 0 ; discriminant D = (-2)2+4*3=16 = 42.
Solutions x1 =(2-4)/ 2 = -1 et x1 =(2+4)/ 2 = 3.
x2-2x-3 < 0 si x appartient à ]-1 ; 3[.
.
|
|




