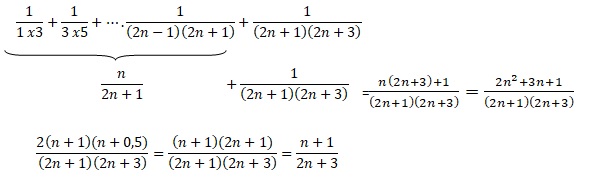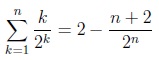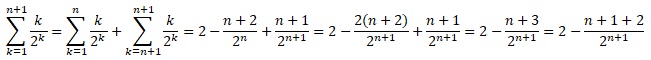Oral mathématiques, concours Advance 2021. Raisonnement par récurrence, suite. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Raisonnement par récurrence.   10. Montrer par récurrence que pour tout entier n non nul : 1 /(1x3)+ 1 /(3 x 5) +....+1 /((2n-1)(2n+1))= n / (2n+1). Initialisation : la propriété est vraie au rang 1. Hérédité : la propriété P(n) est supposée vraie au rang n. Ainsi P(n) =1 /(1x3)+ 1 /(3 x 5) +....+1 /((2n-1)(2n+1))= n / (2n+1). Calcul de P(n+1) : La propriété est vrai au rang n+1. Conclusion : la propriété est vraie au rang 1 et héréditaire ; elle est donc vraie pour tout entier naturel non nul.  11.  Montrer par récurrence que pour tout entier n non nul : 13+33+...+(2n-1)3 = 2n4-n2. Initialisation : la propriété est vraie au rang 1. Hérédité : la propriété P(n) est supposée vraie au rang n. Ainsi P(n) =13+33+...+(2n+1)3 = 2n4-n2. Calcul de P(n+1) : 13+33+...+(2n-1)3 +(2n+1)3 =2n4-n2 +(2n+1)3 ; (2n+1)3 =8n3+12n2+6n+1 ; 2n4-n2 +(2n+1)3 =2n4-8n3+11n2+6n+1. Or 2(n+1)4 -(n+1)2 =(n+1)2 (2(n+1)2-1) =(n+1)2 (2n2+4n+1)=(n2+2n+1)(2n2+4n+1) =2n4-8n3+11n2+6n+1. La propriété est vrai au rang n+1. Conclusion : la propriété est vraie au rang 1 et héréditaire ; elle est donc vraie pour tout entier naturel non nul. 12. Soit a appartenant à R*+. Montrer par récurrence que pour tout entier naturel n : (1+a)n > 1+na. Initialisation : la propriété est vraie au rang 1. Hérédité : la propriété P(n) est supposée vraie au rang n. Ainsi P(n) =(1+a)n > 1+na. Calcul de P(n+1) : (1+a)n+1 = (1+a)n(1+a) > (1+na) (1+a). (1+a)n+1 > 1+na+a+na2. (1+a)n+1 > 1+(n+1)a+na2. Or na2 > 0, donc 1+(n+1)a+na2 > 1+(n+1)a. (1+a)n+1 > 1+(n+1)a+na2> 1+(n+1)a. La propriété est vrai au rang n+1. Conclusion : la propriété est vraie au rang 1 et héréditaire ; elle est donc vraie pour tout entier naturel. 13.  Montrer par récurrence que pour tout entier naturel n : 8n-1 est divisible par 7. Initialisation : la propriété est vraie au rang 1. 81-1 = 7 est divisible par 7. Hérédité : la propriété P(n) est supposée vraie au rang n. Ainsi P(n) =8n-1 est divisible par 7. Calcul de P(n+1) : 8n+1-1 = 8n x8 -1 =8n x(8-1+1) -1 =8n x7 +8n-1. 8n x7 est divisible par 7 ; 8n-1 est divisible par 7. Donc 8n+1-1 est divisible par 7. La propriété est vrai au rang n+1. Conclusion : la propriété est vraie au rang 1 et héréditaire ; elle est donc vraie pour tout entier naturel. 14. Montrer par récurrence que pour tout entier naturel n non nul : Initialisation : 1 / 2 =2-3 /2 =1 /2, la propriété est vraie au rang 1. Hérédité : la propriété P(n) est supposée vraie au rang n. Calcul de P(n+1) : La propriété est vrai au rang n+1. Conclusion : la propriété est vraie au rang 1 et héréditaire ; elle est donc vraie pour tout entier naturel. .... Suites. 15. Soit (un) une suite vérifiant pour tout entier naturel n, un+1=3 un et u15 = 10. a. Déterminer u30. Il s'agit d'une suite géométrique de raison q = 3 ; u15 =u0 x315= 10 ; u30 =u0 x330 =u30 =u0 x315 x 315 =10 x 315 . b. Déterminer u15 +u16 +...+u30. u15 +u16 +...+u30 = u15 (1-331-15) / (1-3)=10(1-316) / (1-3) = -5(1-316). 16. Soit S = 1 /2 +2 +7 /2 +... +19 /2 +11.   Détyerminer S après avoir vérifié que S est la somme de termes consécutifs d'une suite arithmétique. u0 = 0,5 ; u1 =2 =u0+1,5 = 0,5 +1,5 ; u3 =u2 +1,5 =2 +1,5 = 3,5. un = 1,5 +n x1,5 =11 ; n = 10,5 / 1,5 = 7. S est la somme des 8 premiers termes d'une suite arithmétique de raison 1,5 et de premier terme 0,5. S =8 (u0+u7) / 2 =8 (0,5 +11) / 2 = 46. 17.  Soient (un) et (vn) définies pour tout n entier non nul par  : un = 1 +1 /2 +1 /3 +...+1/n et vn = un +1/n. Etudier la monotonie de ces suites. un+1-un =1 +1 /2 +1 /3 +...+1/n +1/(n+1) -(1 +1 /2 +1 /3 +...+1/n). un+1-un =1 / (n+1) positif. La suite (un) est strictement croissante. vn+1 -vn = un+1 +1/ (n+1) -  un -1/n. vn+1 -vn = un+1 -  un +1/ (n+1)-1 /n. vn+1 -vn = 2 /(n+1) - 1 /n. vn+1 -vn =2n-(n+1) / (n(n+1)) =(n-1) / (n(n+1)) positif ou nul. (vn) est croissante. 18.  Soit (un) la suite vérifiant pour tout entier naturel : un+1 = 3un+4 et u0 = 2. Soit (vn) = (un+2). a. Montrer  que (vn) est géométrique. vn+1 = un+1 +2. vn+1 =3un+6 = 3(un+2) = 3 vn. (vn) est géométrique de raison 3 et de premier terme v0 = u0 +2 = 4. b. en déduire (vn) puis (un) en fonction de n. vn = 4 x3n ; un = vn-2 = 4 x3n -2. 19. Soit (un) une suite vérifiant pour tout entier naturel : un+1 = un+6 et u5 = 3. a. Déterminer u20. Cette suite est arithmétique de raison 6. u20-u5 =15 x6 =90. u20 = u5+90 = 3+90 = 93. b. Déterminer u5 +... +u20. Somme de 16 termes de la suite arithmétique : 16 / 2 (u5+u20) =8 (3+93)=768. 20. Soit (un) une suite vérifiant pour tout entier naturel : un+1 = (un +1)½ et u0 = 2. a. Montrer par récurrence que cette suite est décroissante et minorée par 1. Initialisation : u1=(u0+1)½ = 3½ < 2. 1 < u1 < u0 : la propriété est vraie au rang 1. Hérédité : 1 < un+1  < un est supposée vraie. 1+1 < un+1  +1< un +1. La fonction racine carré étant croissante : 2½ < (un+1  +1)½ < (un +1)½. Or 1 < 2½ : 1 < un+2 < un+1. La propriété est vraie au rang n+2. Conclusion : la propriété est vraie au rang 1 et héréditaire, elle est donc vraie pour tout entier naturel. b. Etudier la convergence de cette suite. La suite est décroissante et minorée par 1 : donc elle converge vers une limite notée l.. Quand n tend vers plus l'infini : limite de un+1 = l ; limite de (un+1)½ = (l+1)½. (l+1)½= l ; l2-l-1 =0. Discriminant D = 1+4=5. Solution supérieure à 1 retenue : l=(1+5½) / 2 .

menu