Hydrolienne
à membrane ondulante, concours général Sti2d 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Les
fermes aquacoles sont souvent implantées dans des zones entièrement
dépourvues d'énergie électrique. Une solution innovante ( une membrane
ondulant avec le courant marin) permet de récupérer de l'énergie des
courants marins.
L'énergie électrique produite par une ou plusieurs hydroliennes à
membrane ondulante doit permettre d'alimenter une ferme aquacole
implantée au large de Boulogne sur mer.
Etude du lieu géographique
idéal.
1.1. Relever la
profondeur des fonds marins au niveau de la bouée Ophélie et de la
bouée Bassure de Baas.
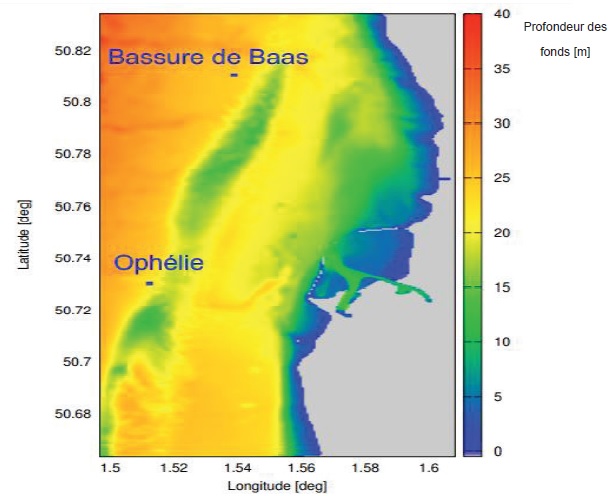
La profondeur des fonds est voisine de 20 m à la bouée Ophélie
et de 28 m à la bouée Bassure de Baas.
Relever la plage de vitesse moyenne du courant marin à 3 m du fond
marin au niveau de ces deux bouées.
Bouée Bassure de Baas : 0,6 m /s pour un coefficient de marée 45 ; 1,2
m /s pour un coefficient de marée 110.
Bouée Ophélie : 0,4 m /s pour un coefficient de marée 45 ;
1,0 m /s pour un coefficient de marée 110.
1.2
Convertir les coordonnées ( latitude et longitude ) exprimées
initialement en degrés-minutes en degrés des lieux suivants : bouée
Ophélie et ferme aquacole susceptible d'être située à proximité
de cette bouée.
Bouée Ophélie
A:
Longitude 1 degré 30,8535 minutes ; 30,8535 / 60 ~0,514 225 degré
; soit 1,514 225 degrés.
Latitude : 50 degrés 43,8652 minutes ; 43,8652 / 60 =0,73109 soit
50,73109 degrés.
Ferme aquacole
B :
Longitude 1
degré 33,8838 minutes ; 33,8838 / 60 ~0,56473 degré ; soit
1,56473 degrés.
Latitude : 50 degrés 43,8652
minutes ; 43,8652 / 60 =0,73109 soit 50,73109 degrés.
Calculer la valeur décimale Vd entre les deux lieux
précédents.
Vd = sin ( lat_A) . sin(lat_B) + cos ( lat_A) . cos (lat_B)
. cos(lon_A -lon_B).
Vd = sin (
50,73109) . sin(50,73109) + cos ( 50,73109) . cos (50,73109) .
cos(1,514225 -1,56473).
Vd =0,59936053
+0,40063947 x0,99999961 =0,999999684.
Déterminer la distance entre la bouée Ophélie et la ferme aquacole
susceptible d'être située à proximité de celle-ci.
D = R arcos (Vd) = 6371 arcos(0,999999684) ~6371 x5,579414 ~3,55
km.
R : rayon de la terre ; 0,99999961 rad.
1.3. Calculer la puissance cinétique
surfacique Pcs (W m-2) disponible pour les différentes
valeurs de vitesse un courant marin ( 0,6 ; 1,5 ; 2,5 m /s ). Conclure.
Pcs = 0,5 r
V3 avec r =
1025 kg m-3 pour l'eau de mer.
vitesse
(m/s)
|
0,6
|
1,5
|
2,5
|
Pcs
(W m-2)
|
110,7
|
1730
|
8008
|
La puissance cinétique
surfacique croît ( est proportionnelle )avec le cube de la
vitesse du courant.
1.4
Déterminer et justifier le lieu le plus approprié pour l'emplacement du
champ hydroliennes à membrane ondulante.
La vitesse moyenne du courant doit être la plus grande possible : bouée Bassure de Baas.
L'hydrolienne à membrane
ondulante.
1.5. Donner le
coefficient de marée le plus défavorable en termes de vitesse du
courant marin permettant d'assurer l'autonomie énergétique d'une ferme
aquacole quelle que soit la période de l'année.
Le coefficient de marée 45 est le plus défavorable ; la vitesse à 3 m
du fond est inférieure à celle du coefficient 110.
1.6. A partir des
dimensions et de l'amplitude tête à creux Atc de la membrane
ondulante, calculer sa surface frontale Sf balayée par le
courant marin.
Atc = 1,6 m ; largeur de la membrane : 2,5 m ; Sf =
Atc fois largeur =1,6 x2,5 =4 m2.
1.7.Calculer la puissance
cinétique moyenne Pc reçue par la membrane à la bouée Bassure de Baas pour le coeffiient de
marée 110.
Pc =Sf x PCs.
Pcs = 0,5 r
V3 = 0,5 x1025 x1,23 =885,6 W m-2 ; Pc
= 4 x885,6 =3542,4 W.
1.8. Donner la valeur du coefficient
de puissance Cp de la membrane ondulante, puis déterminer la
puissance mécanique Pméca produite par celle-ci.
Cp = 0,45 ; Pméca = Cp Pc =
0,45 x 3542,4 =1594 W.
1.9.
En considérant que la puissance mécanique produite par la membrane est
équitablement répartie sur les 6 alternateurs linéaires, en déduire la
puissance mécanique reçue par chaque alternateur.
1594 / 6 = 265,68 W.
Déterminer la puissance en sortie d'un modulateur asservi PEMA.
Rendement d'un alternateur : 70 % ;
rendement du modulateur asservi : 98 %.
365,68 x 0,70 x 0,98 ~182 W.
1.10. Déduire la puissance
électrique totale PET que l'on récupère sur une membrane
dans ces conditions de fonctionnement. Conclure sur la puissance
extraite.
182 x6 = 1093 W, soit environ 31 % de la puissance cinétique reçue.
Optimisation de la
production d'énergie électrique.
1.11. Déterminer les paramètres influents sur la puissance électrique produite par l'hydrolienne à membrane.
La puissance électrique dépend de la vitesse du courant et de la fréquence d'oecillations de la membrane.
Pour un courant de 1,5 m /s et une fréquence d'oscillations de 0,14 Hz, Pélectrique max = 2 kW.
Pour un courant de 2 m /s et une fréquence d'oscillations de 0,18 Hz, Pélectrique max = 5 kW.
Pour un courant de 2,5 m /s et une fréquence d'oscillations de 0,22 Hz, Pélectrique max = 10 kW.
Production d'énergie électrique.
Cette production variera en fonction de la vitesse du courant marin et au coefficient de marée.
Hypothèses d'étude :
Vitesse moyenne du courant vmoy = 0,6 m / s.
Puissance électrique produite par ce courant PET = 137 W.
1.14. Relever le
pourcentage de temps où la vitesse du courant marin est supérieure à sa
vitesse moyenne sur le lieu géographique considéré. En déduire la durée
moyenne en heure par jour de fonctionnement de l'hydrolienne. Calculer
l'énergie électrique moyenne journalière extractible des courants
marins.
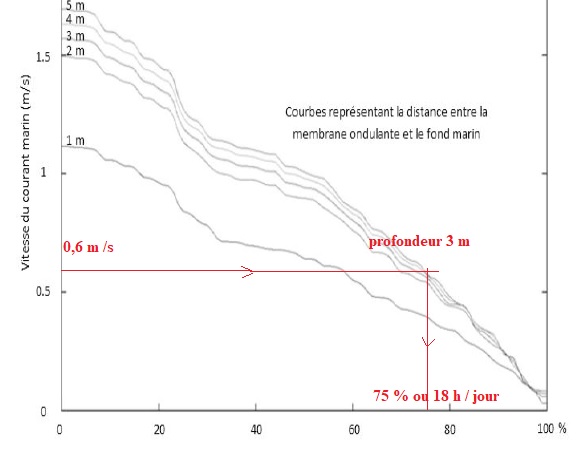
WEMJ (Wh)= PET (W) x durée (h) =137 x 18 =2466 Wh.
1.15. Démontrer que la fréquence du courant marin est f = 0,000046296 Hz.
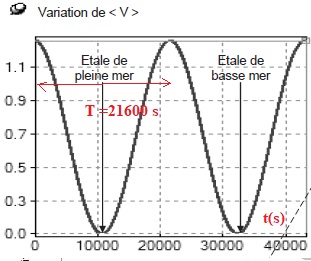
Fréquence (hz) = 1 / période (s) = 1 / 21 600 =0,000046296 Hz.
Donner la plage de variation de puissance électrique lorsque la membrane ondulante est en mouvement.
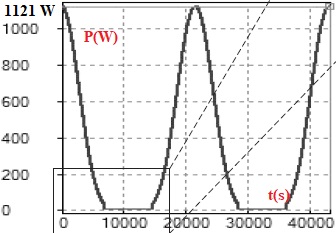
Plage de variation de la puissance : 0 ; 1121 W.
Sur la courbe de variation de l'énergie électrique productible, expliquer à quoi correspondent les zones à palier constant.
Sur une zone à palier constant, la variation d'énergie produite est
constante ; l'énergie produite est alors proportionnelle au temps.
Indiquer l'unité du compteur d'énergie.
Puissance ( W) / (3600 x1000) fois durée (s) ; l'énergie s'exprimme en kWh.
Evaluer l'énergie électrique produite en une journée.
Sur une demi-journée, aire de la partie comprise entre la courbe " variation de puissance" et l'axe des abscisses.
Du fait des symétries : 4 x(1121 x7500) / 2 = 1,68 107 J =1,68 104 kJ =1,68 104 / 3600 kWh ~4,67 kWh par demi-journée.
Soit sur une journée : 4,67 x 2= 9,3 kWh.
|
...
|
....
|
Parc de batteries Rolls. ( 6 V );
Besoin journalier en énergie électrique de la ferme aquacole : 15 kW h j-1.
Tension continue du parc de batteries U = 48 V.
Autonomie du système : un jour sans recharge.
1.17. Déterminer le nombre d'hydroliennes à membrane à installer afin de recharger le parc de batteries.
15 / 9,3 = 1,6 soit 2 hydroliennes.
1.18. Calculer l'énergie du parc de batteries WEPB, en tenant compte de la profondeur de décharge de celles-ci (45 %). En déduire la capacité totale du parc CPB.
WEPB = 15 / (1-0,45) ~27,3 kWh ou 27,3 x3600 =9,82 104 kJ.
CPB = 9,82 104 / 48 =2,045 103 ~2,0 103 k Cou 2,0 103 / 3,6 =5,7 102 kAh.
Quel est le nombre de batteries.
Pour obtenir 48 V, on monte 8 batteries de 6 V en série.
Déterminer la capacité minimale d'une batterie CB.
CB =5,7 102 / 8 ~71 kAh.

L'alternative au fioul.
1.19. La production d'énergie par groupe électrogène au fioul présente des inconvénients. En citer trois.
Emission de dioxyde de carbone ( gaz à effet de serre ) et de particules fines.
Dépendances vis à vis des producteurs de pétrole.
Pollution de l'eau de la ferme aquacole.
1.20. Calculer l'émission directe de CO2 en kg du groupe électrogène en une année.
Emission directe de CO2 : 283 g kW-1 h-1.
Besoin journalier en énergie électrique de la ferme aquacole : 15 kWh j -1.
Emission de CO2 par jour : 283 x15 x24 =1,0188 105 g = 101,88 kg.
Par an : 365 x101,88 ~37 tonnes.
Sollicitations engendrées par la membrane et les câbles.
La membrane de l'hydrolienne transmet des efforts qui sollicitent les
éléments de structure par l'intermédiaire de trois baras encastrés sur
le cerceau et de deux câbles de contrainte. Le modèle de calcul
analytique permet de calculer, pour la membrane, la force de trainée Ft et de portance Fp.
Ft =0,5 Cx r Sf V2 ; Fp =0,5 Cz r Sf V2 ;
r = 1025 kg m-3, masse volumique de l'eau de mer ; V, vitesse du courant avec Vmax = 2,5 m /s ;
Sf = 4 m2 surface frontale ; Cx =0,86 ; Cz = 1,17.
2.1. Calculer les forces de trainée et de portance pour la vitesse de courant maximale.
Ft =0,5 Cx r Sf V2 =0,5 x 0,86 x 1025 x 4 x 2,52 ~1,1 104 N ou 11 kN.
Fp =0,5 Cz r Sf V2 =0,5 x 1,17 x 1025 x 4 x 2,52 ~1,5 104 N ou 15 kN.
2.2.
Pour les situations 1 et 5, la membrane est très inclinée ( courbure
maximale ), les efforts de trainée induits en B sont très importants
aux dates 0,16 s et 2,3 s. Ils ont pour valeur environ 8,5 kN.
Aux mêmes dates, les efforts de portance induits en B sont respectivement de 1,9 kN et -1,9 kN.
2.3. Relever à
l'instant t = 0,8 s, l'effort induit en B par les efforts de trainée et
de portance. En déduire la norme et l'inclinaison par rapport à
l'axe x de l'effort FB(4-->2).
Ft = 3,1 kN ; Fp = 11 kN.
FB(4-->2) = (3,1 2+112)½ =11,5 kN ; inclinaison : arctan ( 11 / 3,1) ~74 °.
2.4. Pour le même instant, relever les efforts de traction Tx et Tz dans chacun des deux câbles. En déduire la norme et l'inclinaison par rapport à l'axe x de l'effort FA(3-->2).
Tz = 1,8 kN ; Tx = -5,6 kN.
FA(3-->2) = (1,8 2+(-5,6)2)½ =5,9 kN ; inclinaison : arctan ( -1,8 / 5,6) ~ 160°.
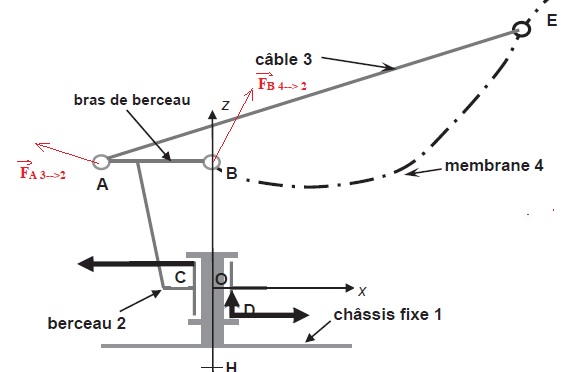
2.5. Identifier le couple force-distance qui affecte le plus la rigidité radiale de la liaison pivot d'axe Oz.
Couple exercé en A. XA = 12 kN et OA = 1 m.
Les actions de liaison en A, B et les actions en G sont équivalentes à une force FM de coordonnées( Fr =16 kN ; Fa = -20,7 kN) appliquée au point M de coordonnées (0 ; 1,35 ). Cette force sollicite la liaison pivot en porte à faux.
2.6. Calculer les pressions de contact pa due à la composante suivant Oz et pr due à la composante suivant l'axe Ox ( effort radial).
pa = 4Fa /(p(D2-d2)) avec D = 0,24 m et d = 0,20 m.
pa =4 x20700 /(3,14(0,242-0,202))~1,5 106 Pa ( 1,5 MPa).
|
|