Mise
en maintien et positionnement d'une barge, étude de la descente à 70 m
de profondeur,
concours général Sti2d 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
...
|
.
.
|
..
..
......
...
|
Localisation de
la barge.
Le positionnement est guidé par le système GNSS. Les déplacements de la
barge évolueront en fonction du dragage à réaliser.
3.1et 2 Compléter
le tableau en donnant la fréquence des deux ondes porteuses.
1575,42 MHz pour L1 et 1227,60 MHz pour L2.
|
Fréquence
f ( MHz)
|
période
T
|
longueur
d'onde l
|
L1
|
1575,42
|
1
/ (1575,42 106)=6,35 10-10 s
|
3
108 x 6,35 10-10
=0,19 m
|
L2
|
1227,60
|
1 /
(1227,62 106)=8,15 10-10 s |
3 108 x 8,15 10-10 =0,24 m |
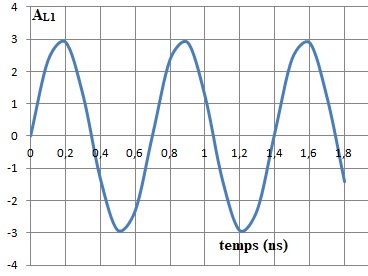
3.3. Tracer le signal de la porteuse
L1 appelé SL1 et défini tel que : SL1
= AL1 sin ( wt).
Prendre 3 carreaux pour AL1 ; w = 2p f =6,28 x (1575,42 106)~9,9
109 rad /s.
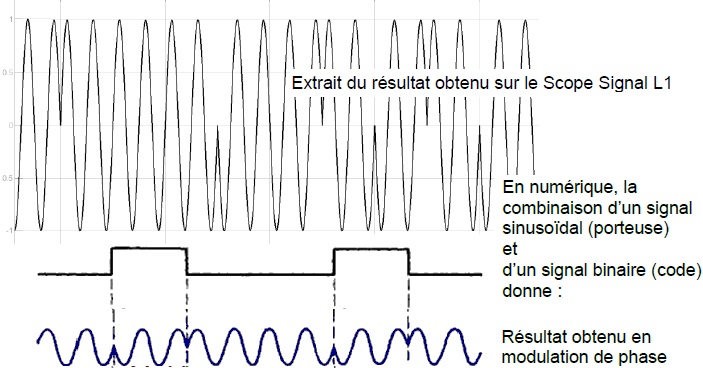
3.4 Identifier le
type de modulation utilisé.
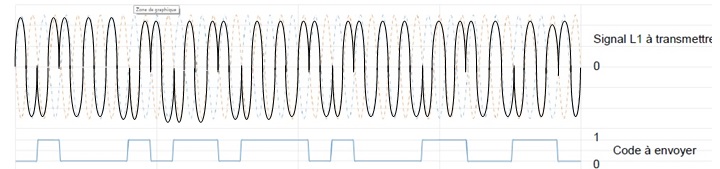
3.5. Tracer le
signal modulé correspondant au code à envoyer.
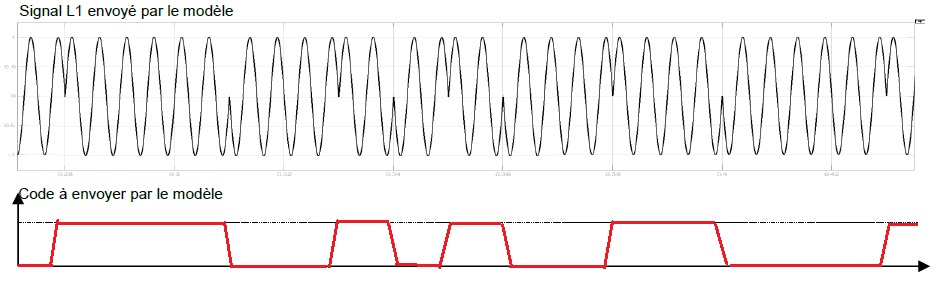
3.6. Tracer le code
à envoyer correspondant à l'extrait de signal de la simulation. La
séquence de code cpùùence par zéro.
Le
réseau Profinet est configuré grâce au logiciel STEP - 7. Il permet
d'attribuer un nom et une adresse IP à chaque appareil possédant une
adresse MAC.
3.7. Déterminer si
le réseau étudié est un réseau LAN, MAN ou WAN.
Réseau local LAN.
Une adresse MAC ( exemple 08-00-06-6B-80-C0) permet d'identifier
spécifiquement chaque appareil. Les trois premiers octets renseignent
sur le constructeur et les trois derniers sur l'identification de
l'appareil.
3.8. Calculer le
nombre de constructeurs que ce système d'identification permet
d'attribuer.
3 octets soit 3 x8 = 24 bits et 224 =16 777 216
constructeurs.
Une adresse @IP et un masque sous-réseau (M) sont attribués à chacun
des appareils associés du réseau Profinet.
L'adresse deréseau @R résulte de la combinaison logique ET ( opérateur
& qui effectue un ET logique entre chaque bit de même rang) entre
le masque M et l'adresse @IP
@R =@IP & M.
La configuration d'un des appareils est : @IP = 172.30.100.15 ; M =
255.255.192.0
3.9. Convertir en binaire l'adresse
@ IP.
15 = 23 +22 +21+1 soit en binaire : 00001111
100 = 0x27 + 26 +25+0x24
+0x23+1x22+0x2+0 soit 01100100.
30=0x27 +0x 26 +0x25+1x24
+1x23+1x22+1x2+0 soit 00011110.
172=1x27
+0x 26 +1x25+0x24 +1x23+1x22+0x2+0
soit 10101100.
10101100.00011110.01100100.00001111.
3.10.
Convertir en bilaire le masque de sous-réseau M.
255=1x27
+1x 26 +1x25+1x24 +1x23+1x22+1x2+1
soit 11111111.
192=1x27
+1x 26 +0x25+0x24 +0x23+0x22+0x2+0
soit 11000000.
11111111.11111111.11000000.00000000
3.11.
Effectuer en binaire, l'opération donnant l'adresse @IP.
10101100.00011110.01000000.00000000
3.12. Convertir en
décimale cette adresse @R.
10101100 : 27+0x26+1x25+0x24+1x23+1x22+0x2+0
soit 172.
00011110 : 0x27+0x26+0x25+1x24+1x23+1x22+1x2+0
soit 30.
01000000 :0x27+1x26+0x25+0x24+0x23+0x22+0x2+0
soit 64.
172.30.64.0
3.13. Préciser l'appellation et le
rôle de l'adresse @IP =172.30.127.255 dans ce réseau.
Les deux premiers nombres identifient le
réseau ; les deux derniers identifient l'hôte spécifique.
3.14. Calculer le
nombre d'appareils maximums que peut contenir ce réseau.
2 octets soit 16 bits soit 216 = 65 536 appareils.
Stabilisation de la barge.
3.15. Justifier le choix d'une structure porteuse en acier inoxydable pour le caisson.
L'impact environnemental des matériau doit être le plus faible possible.
L'oxydation par le dioxygène et l'eau doit être évitée.
Les métaux sont denses, résistants et ductiles.
3.16. Donner la hauteur maximale immergée autorisée pour éviter la présence d'eau sur la barge.
Le tirant d'eau maximum ( hauteur immergée du caisson ) est égal à 1,50 m.
3.17. Déterminer la masse maximum que pourra supporter un caisson.
Longueur du caisson : 6,058 m ; largeur : 2,436 m ; hauteur : 1,8 m ; masse du caisson : 5350 kg.
Volume du caisson immergé : V = 1,5 x 2,436 x 6,058 =22,136 m3.
Poussée d'Archimède due à l'eau : V reau g =22,136 x 1000 x9,81 =2,17 105 N.
Le poids du système { caisson + charge de masse m } est opposé à la poussée d'Archimède.
2,17 105 = (m +5350) x9,81 ; m ~1,68 104 kg ou 16,8 tonnes.
Par sécurité, pour la suite des calculs, la masse maximale supportée par un caisson sera prise égale à 16,5 tonnes.
Les 4 faces d'un caisson sont reliées par un réseau de poutrelles.
Chaque extrémité de poutrelle est articulée aux parois du caisson. Les
poutrelles de 1 à 3 repossent sur les poutrelles A à F. La charge sera
répartie de manière homogène sur la surface du caisson.
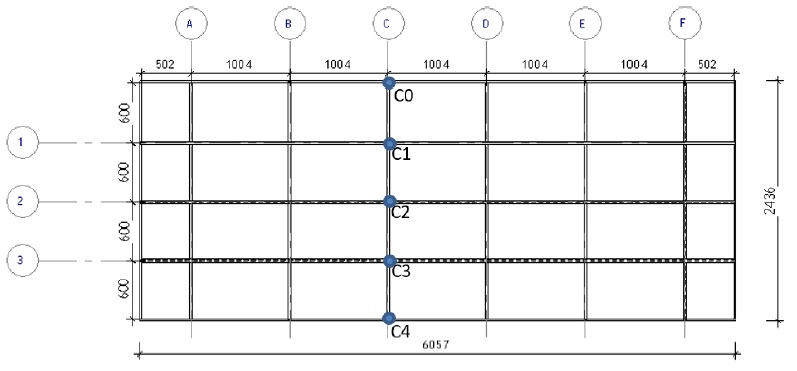
3.18. Déterminer la valeur de la charge reprise par les poutrelles de 1 à 3 en kN / m..
Chacune de ces poutrelles 1, 2 et 3 reposent sur les 6 appuis, poutrelles A, B, C, D, E et F.
Chaque poutrelle 1, 2, 3 supporte le tiers du caisson.
Poids de la charge maxi : 16500 x9,81 ~ 1,62 105 N = 162 kN.
Charge répartie sur une poutrelle : 162 / 3 =54,96 kN.
Longueur des poutrelles : 6,057 m ; 54,96 / 6,057 ~8,91 kN / m.
Il s'agit maintenant de dimensionner les poutrelles A à F. Toutes les poutrelles sont identiques.
3.19. Parmi ces 6 poutrelles, préciser celles qui sont le plus sollicitées et qui permettront le dimensionnement.
Les poutrelles B, C, D et E sont les plus sollicitées, la largeur de la reprise étant de 1,004 +1,004 = 2,008 m.
Les poutrelles A et F sont les moins sollicitées, la largeur de la reprise étant de 1,004 +0,502 = 1,506 m.
|
...
|
....
|
Etude de la descente à 70
m de profondeur.
La
benne doit descendre en chute libre pour permettre une pénétration
maximale dans les sédiments tandis que le robot doit accoster le fond
avec une vitesse maximale à ne pas dépasser pour ne pas être endommagé.
4.1. Décrire les exigences relatives au contact avec le sol pour les deux solutions envisagées.
Benne en chute libre, vitesse maximale sans freinage.
La vitesse maximale du robot au moment de l'impact doit être de 0,1 m /s.
4.2. Déterminer la nature du mouvement de la benne par rapport au sol au moment de l'impact.
La benne est en mouvement rectiligne uniforme ( vitesse constante).
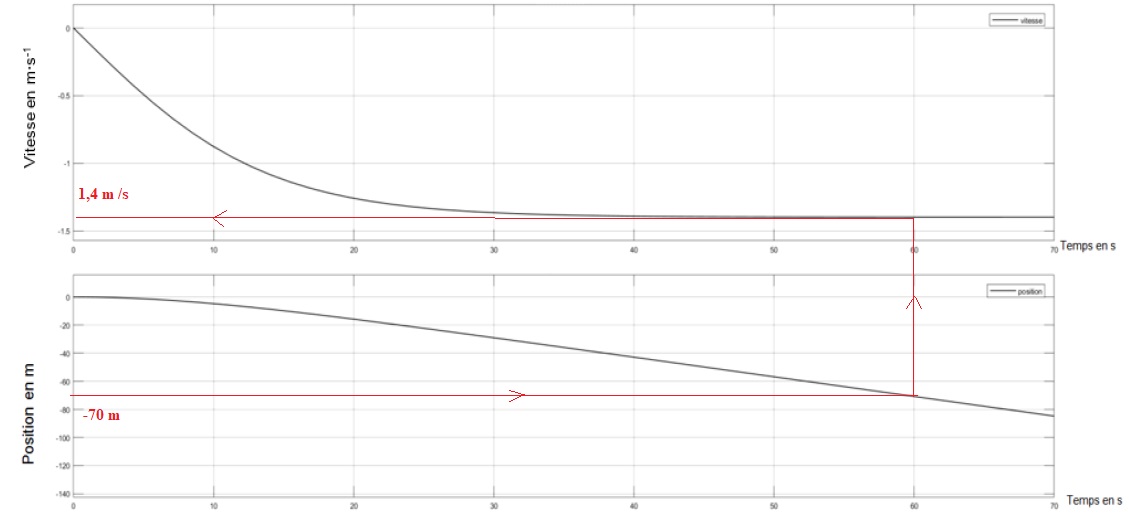
4.3. Calculer l'énergie cinétique de la benne au moment de l'impact.
Ec = ½mv2 avec m =9305 kg.
Ec = 0,5 x9305 x1,42 =9,12 103 J.
4.4. Conclure quant aux conditions d'impact.
L'énergie cinétique de la benne étant supérieure à 7000 J au moment de l'impact, la condition est validée.
Lors de la phase de descente le robot est freiné par deux câbles reliés
à deux treuils qui permettent de maitriser la vitesse de descente.
4.5. A l'aide des courbes suivantes obtenues par simulation, expliquer les différentes étapes de la descente du robot.
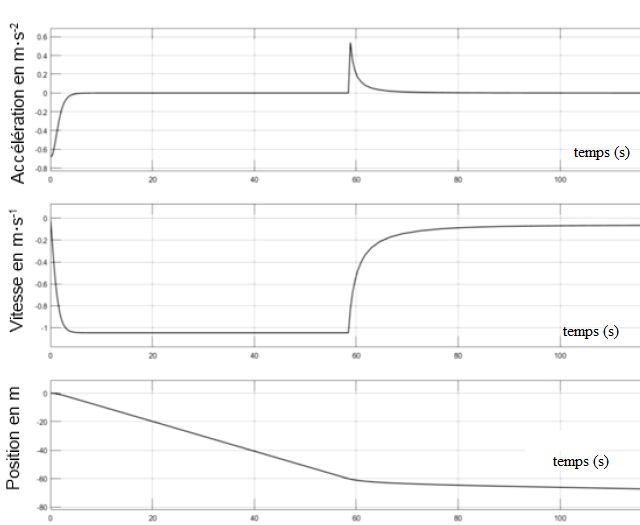
Durant les premières secondes de chute, le robot est en chute libre puis sa vitesse se stabilise vers 1,2 m /s.
A partir de 58 s, le robot est freiné, sa vitesse atteint 0,08 m /s à t
= 80 s ; le mouvement du robot est alors rectiligne uniforme. La
profonfeur est de 65 m.
4.6. Expliquer en quoi le modèle simulé correpond ou non au cahier des charges ( vitesse maximale du robot au moment de l'impact doit être de 0,1 m /s).
Ce modèle simulé correspond au cahier des charges pour la vitesse d'impact ( 0,1 m /s maxi ).
4.7. Représenter qualitativement :
- la résultante des actions des câbles sur le robot ramenés au seul point A ;
- le poids du robot en G ;
- la poussée d'Archimède en B ;
- l'action de trainée de l'eau sur le robot en C.
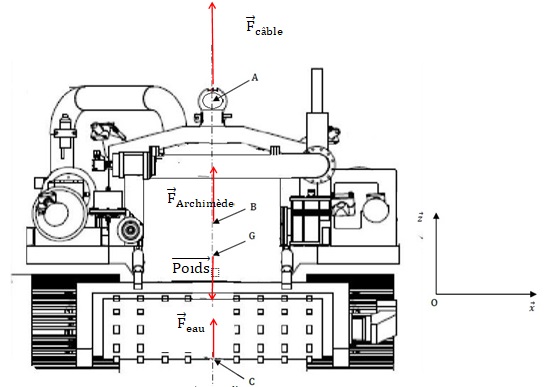
4.8 Ecrire en G, les torseurs des actions mécaniques agissant sur le robot lors de la descente.
Masse du robot 19 t
Il
faut trouver les coordonnées de chaque forces dans le repère (G, x, y,
z) ainsi que celles des moments des forces calculés en G.
Toutes les forces étant sur la verticale passant par le point G, les moments de toutes les forces calculés en G sont nuls.
Poids, verticale, vers le bas, valeur mg = 19 103 x9,81 ~ 1,86 105 N.
Coordonnées ( 0 ; 0 ; -1,86 105 ).
Poussée d'Archimède, verticale vers le haut, valeur : Volume robot x masse volumique de l'eau x 9,81.
Volume du robot : 11,32 m3.
11,32 x 1000 x9,81 ~1,11 105 N.
Coordonnées ( 0 ; 0 ; 11 105).
Action de l'eau sur le robot, verticale vers le haut, valeur 0,6 S reau v2.
S = 20,13 m2, surface projetée du robot ; v = 1,2 m/s, vitesse de descente du robot.
0,6 x 20,13 x1000 x1,22 =1,74 104 N.
Coordonnées ( 0 ; 0 ; 1,74 104).
4.9. Appliquer le principe fondamental de la dynamique au robot en cours de descente avec une accélération aG.
En projection sur l'axe vertical ascendant :
Fcable +Farchimède +Feau -poids = masse robot aG.
Fcable +1,11 105 +1,74 104 -1,86 105 = 19 103 aG.
Fcable -5,86 104 = 19 103 aG.
4.10. Déterminer la valeur de la force exercée par le câble sur le robot sachant que aG maxi =0,55 m s-2.
Fcable =5,86 104 + 19 103 x0,55 =6,91 104 N.
4.11. Proposer une
modification de la commande du freinage permettant de rduire l'effort
sur le câble lors de la phase de freinage avant le contact avec le sol.
Freinage plus progressif ( durée plus grande) avec une valeur maximale plus faible.
Pour la suite on considère que Fcable = 81 103 N.
4.12. Le câble est
en acier avec une limite élastique de 295 MPa. Déterminer le diamètre
minimum du câble à prévoir pour obtenir un coeeficient de sécurité égal
à 2.
smax = 81 103 / (2 section).
smax =295 / 2 = 147,5.
section = 81 103/ (295 106) =2,74 10-4 m2.
pd2 / 4 = 2,74 10-4 ; d = 1,87 10-2 m ou 18,7 mm.
4.15. Conclure sur le choix de la solution d'enlèvement des sédiments
Robot :
Anantages : nettoyage en continu, accès précis à toute la zone ; pas de pertes de temps en montée et descente.
Inconvénients : contrôle précis lors de la descente ; nécessite une pompe puissante pour remonter les sédiments.
Benne :
Avantages : solution plus simple, moins onéreuse.
Inconvénients : temps perdu lors des descentes et remontées ; la zone est nettoyé par point et non pas en continu.
|
|







