Le virus covid 19, test PCR, perte d'odorat, pousse seringue, scanner thoracique, congelation des vaccins, école de santé des armées ESA 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . Exercice 1. (3,5 points) L'une des étapes du test PCR nécessite un marquage du matériel génétique vrai : la méthode actuelle utilise un marquage par des molécules fluorecentes mais à l'origine il se faisait grâce à des isotopes radioactifs, notamment le noyau 3215P. 1. 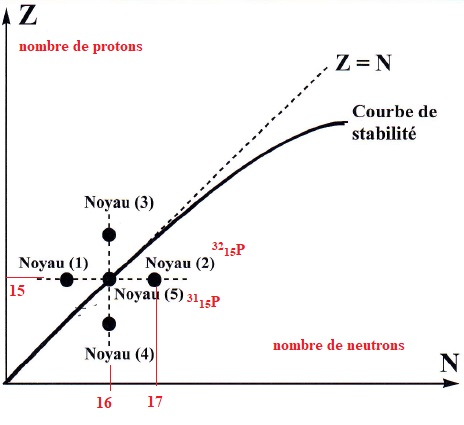On représente le diagramme (Z-N) où 5 noyaux sont identifiés. Le noyau (5) correspond à l'isotope stable de l'élément phosphore. Indiquer en justifiant le noyau correspondant à l'isotope radioactif 3215P. 3215P : 15 protons et 32-15 = 17 neutrons. 3115P isotope stable : 15 protons et 31-15 = 16 neutrons. 2. La désintégration du noyau 3215P conduit au noyau 3216S. a. Ecrire l'équation de désintégration du phosphore 32. Nommer le type de radioactivité. 3215P --> 3216S +0-1e.( béta moins, émission d'un électron ) 3. Pour les marquages journaliers, on dispose d'une activité initiale A0 =0,3 MBq en phosphore 32. l = 6 10-7 s-1. a. Calculer le nombre initial de noyaux. N0 = A / l = 0,3 106 / (6 10-7) =3 / 6 1012 = 5 1011. b. Calculer en seconde, le temps pour que l'activité baisse de 70 %. On donne -ln 0,3 = 1,2. Loi de décroissance radioactive A =A0 exp(-lt).  0,3 A0 =A0 exp(-lt) ; ln 0,3 = -lt ; t = -ln 0,3 / (6 10-7) = 1,2 /(6 10-7) =0,2 107 = 2 106 s. Exercice 2. (4,5 points ) La perte de l'odorat serait liée à une atteinte du bulbe olfactif qui est le lieu de convergence des différents neurones lfactifs. Les fibres nerveuses peuvent être modélisées par le circuit RC ci-dessous où R est la résistance électrique de l'axone, C la capacité de sa membrane et G un générateur de  tension représentant le signal électrique nerveux. Le condensateur est déchargé à t = 0 et le générateur fournit une tension continue E= 70 mV. C = 100 pF ; on donne e-1 ~0,37 et e ~2,72. 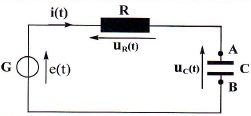1. Donner le signe des charges qA(t) et qB(t) portées par lea armatures en justifiant. A est relié à la borne positive du générateur : qA(t) >0 ; B est relié à la borne négative du générateur : qB(t)  < 0. 2. Etablir la relation entre l'intensité i(t) et la tension uc(t) aux bornes du condensateur. qA(t) = C uc(t) et i(t) = dqA(t) / dt = C duc(t) / dt. 3. Montrer que la tension aux bormnes du condensateur vérifie l'équation différentielle : duc /dt + a uc = ß. Loi d'additivité des tensions : E = uR(t) +uc(t) avec uR(t) = R i(t) = RCduc(t) / dt. RCduc(t) / dt + uc = E. duc(t) / dt + uc / RC) = E / (RC). On identifie a = 1 /(RC) et ß = E / (RC). 4.  Résoudre l'équation et donner l'exppression de uc(t). Solution générale de l'équation sans second membre : uc(t) = A exp(-at) avec A une constante. Solution particulière : uc(t) = E. uc(t) = A exp(-at) + E. uc(t=0) = A +E = 0 soit A = -E. uc(t) = -E exp(-at)+E = E(1-exp(-at)). 5. Le graphe ci-dessous représennte uc(t). Déterminer graphiquement la constante de temps t du circuit et en déduire R. 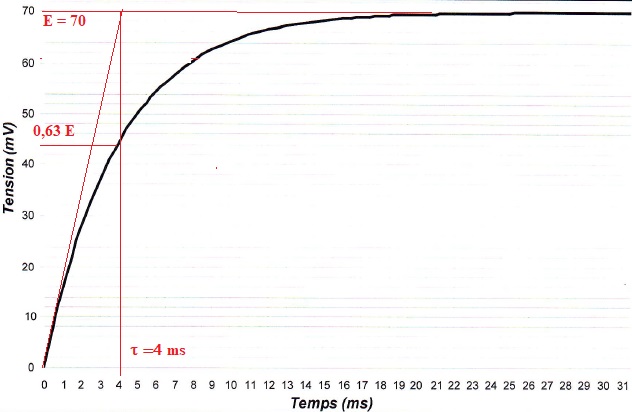R = t / C =4 10-3 / (100 10-12) =4 107 ohms. Exercice 3. ( 2 points ). Dans les formes les plus graves de Covid-19, le patient doit être mis en coma artificiel pour assurer sa ventilation pulmonaire par intubation. l'administration de médicaments se fait par un pousse-seringue électrique formé d'une seringue dont l'extrémité est reliée à une tubulure elle même reliée à la veine du patient via un cathéter. On suppose que le liquide injecté vérifient les hypothèses nécessaires pour écrire la conservation du débit volumique et pour la relation de Bernoulli. 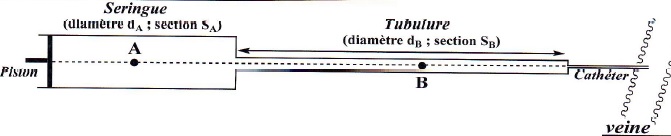Diamètre de la seringue et de la tubulure : dA = 2 cm ; dB = 1 cm. Vitesse d'écoulement du liquide dans la seringue : vA = 5 cm / s. Prende p ~ 3. Relation de Bernoulli : P1 +r g z1 +½ r v12 = P2 +r g z2 +½ r v22 . 1. Calculer en m3 / s la valeur du débit volumque en A. Section en A : p d2A / 4 ~3 x0,022 /4 =3 10-4 m2. vA = 0,05 m /s ; débit volumique en A : Section x vitesse = 3 10-4 x 0,05 = 1,5 10-5 m3 /s. 2. Calculer la valeur de la vitesse d'écoulement, en cm / s, du liquide en B. Conservation du débit volumique : 1,5 10-5 = SB vB. SB = p d2B / 4 ~3 x0,012 /4 =7,5 10-5 m2. vB =1,5 10-5  / (7,5 10-5) =1,5 / 7,5 =1 /5 = 0,2 m /s = 20 cm /s. 3.  La pression en B est-elle inférieure,égale ou supérieure à celle en A ? Justifier. Relation de Bernoulli : PA +r g zA +½ r vA2 = PB +r g zB +½ r vB2 . Seringue horizontale : zA=zB. PA +½ r vA2 = PB +½ r vB2 . vB > vA, donc PA > PB. Exercice 4. (5 points). Au début de la pandémie de Covid 19, le scanner thoracique a été l'examen de référence pour juger la sévérité de la pneumopathie. Cet examen montra ses limites face à l'afflux de malades et la nécessité de respecter les règles hygièniques barrières. Les médecins développèrent une méthode utilisant un échographe portatif pour évaluer la sévérité de l'atteinte pulmonaire. QCM 1 et 2. On considère une sonde émettant des ultrasons de fréquence 3 MHz ; elle est appliquée sur la surface du thorax d'un patient au niveau d'un  espace intercostal de 2 cm d'ouverture. Avant d'atteindre les poumons, les ultrasons traversent un tissu musculaire de 4 cm d'épaisseur à une vitesse de 1500 m /s. 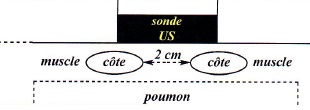QCM 1 ( 2points) Les ondes ultrasonores émises par la sonde ont une intensité sonore de 10-2 W m-2 et on suppoose que le tissu musculaire absorbe une partie de cette intensité à raison de 2,5 dB / cm. Que vaut l'intensité des ultrasons arrivant au niveau des poumons ? Aide : 10-2,5 ~3 10-3 ; 10-9,5 ~3 10-10 ; log(2) ~0,3. A. I = 1 10-21 Wm-2 ; B. I = 3 10-10 Wm-2 ; C. I = 1 10-3 Wm-2 vrai ; D. I = 3 10-3 Wm-2 ; E. les items A, B, C, D sont faux. Niveau d'intensité sonore initial : L = 10 log(10-2 / 10-12) =100 dB Atténuation : 2,5 x 4 = 10 dB. Niveau d'intensité sonore à l'arrivée sur les poumons : 100-10 = 90 dB. I = 10-12 x 109 = 10-3 W m-2. QCM 2. (1 point). Indiquer la ( les) proposition(s) juste(s) parmi les items suivants : A. La longueur d'onde des ultrasons dans le muscle est 5 10-4 m. Vrai. l = v / f = 1500 / (3 106) =15 / 3 10-4 = 5 10-4 m. B. La longueur d'onde des ultrasons dans le muscle est 2 103 m. C. Le faisceau ultrasonore n'est pas diffracté à la traversée de l'espace intercostal. Vrai. 2 cm diffère énormément de la longueur d'onde. D. Le faisceau ultrasonore est diffracté à la traversée de l'espace intercostal. E. Les items A, B, C et D sont faux. QCM 3. (2 points) La sonde est constituée d'un cristal piézoélectrique sur la surface duquel on identifie deux sources ponctuelles S1 et S2 émettant  des ultrasons qui interfèrent au point M. La différence de marche vaut d = 3 cm. la sonde possède trois réglages fréquentiels dont les longueurs d'onde associées sont 1,2 cm, 1,5 cm, 1,8 cm. A. Pour le réglage 1,2 cm, les deux ondes interfèrent de façon destructive. Vrai. 3 / 1,2 =2,5 , nombre impair de demi-longueur d'onde. B. Pour le réglage 1,2 cm, les deux ondes interfèrent de façon constructive. C. Pour le réglage 1,5 cm, les deux ondes interfèrent de façon constructive.Vrai. 3 / 1,5 =2 , nombre entier de longueur d'onde. D. Pour le réglage 1,8 cm, les deux ondes interfèrent de façon destructive. 3 / 1,8 =1,66 , diffère d'un nombre impair de demi-longueur d'onde. E. Les items A, B, C et D sont faux. Exercice 5. (5 points). Le premier vaccin à avoir été commercialisé fut celui des sociétés Pfizer / BioNTech qui nécessita une logistique de distribution particulière puisqu'il devait être conservé à -80°C dans un super-congelateur. QCM 4. (2 points ). Principe d'un congelateur  : un moteur fournit un travail W au fluide caloporteur pour qu'il puisse extraire une quantité de chaleur Q1 du compartiment froid et transférer une quantité de chaleur Q2 vers le milieu extérieur. L'énergie interne du fluide à la fin de la transformation retrouve la valeur qu'elle avait au départ, au cours d'un cycle. | W| = 50 kJ ; |Q1| inconnue ; |Q2| =80 kJ. A. DU = 0. Vrai. B. W = +50 kJ. Vrai. C. Q2 = -80 kJ. Vrai. D. Q1 = +120 kJ. Q1 +Q2 +W = 0 ; Q1 = -50 +80 = 30 kJ. E. Les items A, B, C et D sont faux. QCM 5. (1 point). Le protocole d'utilisation du vaccin impose de décongeler la solution vaccinale en plaçant le flacon dans un réfrigérateur dont la température est comprise entre 2°C et 8°C. La variation d'énergie interne de 0,2 g de solution vaccinale congelée vaut +56 J lorsque la température passe de -80 à -10°C. Aide : 56 / 70 ~ 0,8 ; 56 / 90 ~0,6. A. La convection intervient pour chaufer l'intérieur du flacon. Vrai. B. La variation de température de la solution congelée vaut 333 K -10 -(-80) = 70 degrés. C. La capacité thermique massique de la solution congelée est environ 2,8 J g-1 °C-1. Q = mc DT ; c = 56 / (0,2 x 70) =56 /35 = 5 x56 / 70 ~5 x0,8 =4 J g-1 °C-1. D. La capacité thermique massique de la solution congelée est environ 4 J g-1 °C-1.Vrai. E. Les items A, B, C et D sont faux. QCM 6 et 7. Lorsque la solution est décongelée, le protocole impose de la diluer 10 fois en utilisant une solution de chlorure de sodium à 0,9 %. l'ajout de cette solution comprime l'air stérile emprisonné dans le flacon loors de sa fabrication ; on assimilera l'air stérile dans le flacon à un gaz parfait. QCM 6. (0,5 point) A. La pression est une mesure macroscopique de l'énergie cinétique des molécules. ( la température est liée à l'énergie cinétique) B. Le modèle du gaz parfait ne fait pas la différence entre les structures des molécules N2 et O2. Vrai. C. Un gaz réel se trouvant à faible température et à haute pression est assimilable à un gaz parfait. Un gaz réel est assimilable à un gaz parfait à faible pression. D. L'énergie interne d'un gaz parfait se limite aux énergies cinétiques de ses molécules. Il faut ajouter l'énergie interne de chaque molécule ( rotation, oscillation) E. Les items A, B, C et D sont faux. QCM 7. (1,5 point) Avant dilution, l'air emprisonné présente un volume de 2,8 10-6 m3 et se trouve à une température de 280 K et une pression de 105 Pa. La dilution de la solution comprime l'air emprisonné de manière isotherme, doublant la valeur de la pression. On prendra R ~8 J K-1mol-1. A. La température finale de l'air emprisonné est de 7°C. La transformation est isotherme. B.  le volume final de l'air emprisonné est 1,4 mL. Vrai. Loi de Mariotte : PV = cste. PiVi = PfVf  = 2 PiVf  ; Vf =1,4 10-6 m3= 1,4 mL. C. Le nombre de mole d'air emprisonné est de 1,25 10-4 mole. Vrai. n = PV / (RT) = 105 x2,8 10-6 / (8 x280)=0,28 / (8 x0,28 103) =10-3 / 8 = 1,25 10-4 mole. D. Le nombre de mole d'air emprisonné est de 1,00 10-3 mole. E. Les items A, B, C et D sont faux.

menu