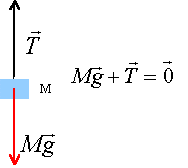Physique,
concours EMIA 2020. Ecole militaire interarmes.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
...
.....
|
Etude d'un ressort.
1.1. Etude statique.
Le ressort est accroché à une potence. Il est de masse négligeable. A
son extrémité libre on suspend des masses de différentes valeurs. Pour
chaque masse, on mesure l'allongement du ressort.
m (kg)
|
0
|
0,2
|
0,4
|
0,5
|
0,7
|
1
|
allongement Dl (cm)
|
0
|
5
|
10
|
12,5
|
17,5
|
24,9
|
1. Tracer la courbe Dl en fonction de la masse m. Donner la relation entre Dl et m.
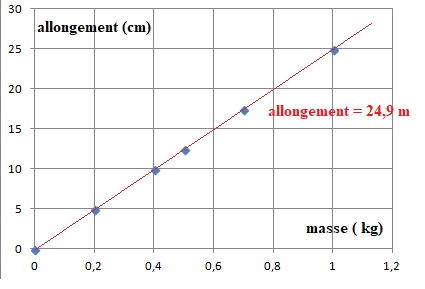
Dl = 24,9 m avec Dl en cm et m en kg.
Dl = 0,249 m avec Dl en m et m en kg.
2. Faire un schéma du ressort avec la masse accrochée et représenter les forces qui s'exercent sur la masse.
3. A l'équilibre écrire la relation entre ces forces.
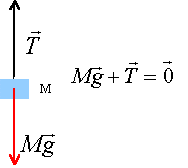
4. En déduire l'expression littérale de la constante de raideur k du ressort.
5. Donner le résultat numérique avec l'unité.
mg = kDl ; k = mg / Dl.
k = 9,81 / 0,249 =39,4 ~39 N /m.
1.2. Etude dynamique.
On utilise le même ressort. Il est fixé à une extrémité à un bâti fixe
et à l'autre à une masse M. Celle-ci se déplace sans frottement sur un
axe horizontal. On repère la position de son centre d'inertie G par son
abscisse x sur cet axe. l'origine de l'axe est la position d'équilibre
du ressort.
A un instant pris comme origine des temps, la masse est écartée de sa position d'équilibre et lâchée sans vitesse initiale.
6. Décrire le mouvement du système.
Osciilations libres non amorties.
7. Faire un schéma des forces qui s'exercent sur la masse M à un instant t.
8. En appliquant la seconde loi de Newton, montrer que l'équation différentielle du mouvement de la masse M s'écrit : x" +w02x=0.
9. En déduire l'expression de la pulsation w0 en fonction de k et M.
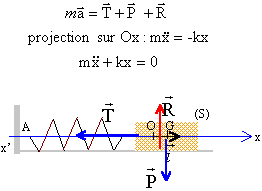 w0
w0²= k /M ; w0 = (k / M)½.
10. Quelle est l'unité de la pulsation ?
La pulsation s'exprime en rad s-1.
11. Donner l'expression de la période propre T0 en fonction de k et M.
w0 = 2p / T0 ; T0 = 2p (M / k)½.
12. On mesure la durée de 10 oscillations. On trouve 10,6 s. Quelle est la valeur de T0 ?
T0 = 1,06 s.
La masse précédennte est surchargée d'une masse m fixée sur M. ce
nouveau système est mis en oscillation comme le précédent. La
nouvelle durée de 10 oscillations est 10,7 s. La surcharge m est égale
à 20 g.
13. Exprimer la nouvelle période T1 en fonction de M, m et k.
T1 = 2p ((M+m) / k)½.
14. En déduire l'expression de k en fonction de T0, T1 et m.
T1 2=4p2(M+m) / k ; T0 2=4p2M / k ;
4p2M / k=T0 2 ; T1 2=T0 2 +4p2m / k ;
T1 2-T0 2 = 4p2m / k ; k = 4p2m / (T1 2-T0 2 ).
15. Calculer k et la comparer à la valeur trouvée par la méthode statique.
k = 4 x3,142 x0,020 /(1,072-1,062) =37,06 ~ 37 N /m.
Ecart relatif : (39,4-37,06) / 37,06 ~0,06 (6 %).
|
.
.
|
Electrocinétique.
2.1 Analyse d'un circuit.
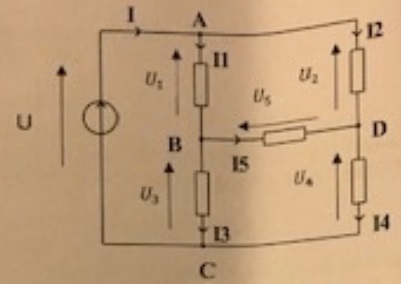
U = 20 V ; I1 = 3 A ; I2 = 4 A ; I5 = 1 A ; U3 = 12 V ; U4 = 5 V.
1. Calculer I, I3 et I4.
Loi de noeuds en A : I = I1 +I2 = 3+4=7 A.
Loi de noeuds en B : I1 = I3 +I5 ; I3 = 3-1=2 A.
Loi de noeuds en D : I4 = I2 +I5 ; I3 = 4+1=5 A.
2. Calculer U1, U2 et U5.
Additivité des tensions : U = U1+U3 ; U1 = 20-12=8 V.
U = U2+U4 ; U2 = 20-5=15 V.
U3 = U4+U5 ; U5 = 12-5=7 V.
2.2. Mesure d'inductance.
l'étude est réalisée en courant continu. On dispose d'une bobine d'inductance L et de résistance r inconnues.
On la place dans un circuit en série avec une résistance R de 50 ohms.
Le circuit est alimenté par un générateur de tension de fem E = 6 V.
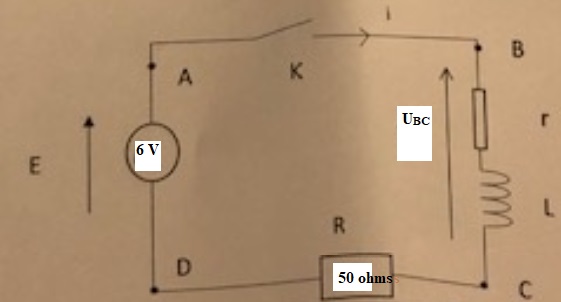
1. Quelle est l'unité d'une inductance ?
henry ( H).
2. Exprimer UBC en fonction de i, L et r.
UBC = ri + L di / dt.
3. En appliquant la loi des mailles, montrer que le courant i vérifie l'équation différentielle di /dt +ai = ß.
4. Donner les expressions de a et ß.
E = Ri +ri+Ldi / dt.
di / dt +(R+r) / L i = E / L.
On pose a = (R+r) / L et ß= E / L.
5. Quelle est l'unité de la constante a ?
a : constante de temps exprimée en s-1.
6. Montrer qu'en régime permanent le courant i tend vers une valeur constante I0 fonction de r, R et E.
En régime permanent di/dt = 0.
I0 = E /(R+r).
7. En régime permanent UCD = 5 V. En déduire la valeur de I0 puis de r.
UCD = RI0 ; I0 = 5 / 50 = 0,1 A.
R+r = E / I0 = 6 / 0,1 = 60 ; r = 60-50 = 10 ohms.
8. Déterminer la solution i(t) de l'équation différentielle.
Solution générale de di /dt +ai =0 : i(t) = A exp(-at) avec A une constante.
Solution particulière i(t) = I0.
i(t) =A exp(-at) +I0.
Quand t =0, i(0) = 0 = A exp(0) +I0= A +I0 ; A = -I0.
i(t) = 0,1(1- exp(-at)).
9. Tracer l'allure de la courbe.
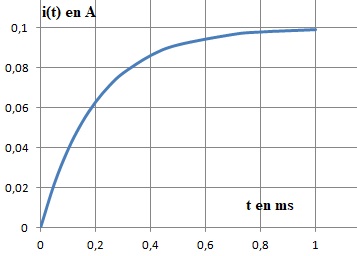
10. L'intensité i atteint 63 % de sa valeur maximale à t = 0,2 ms. En déduire la valeur de L.
0,1 x0,63 = 0,1 (1-exp(-ax2 10-4) ).
0,63 = 1-exp(-ax2 10-4).
0,37 = exp(-ax2 10-4) ; ln(0,37) = -ax2 10-4 ; a= -ln(0,37) / (2 10-4) =4971 s-1.
(R+r) / L = 4971 ; L = 60 / 4971 ~0,012 H.
|
..
.
|
. .
|
Exercice 3.
La
houle est une onde mécanique progressive et périodique. Sa propagation
à la surface de l'eau peut être caractérisée par une période T, une
longueur d'onde l
et sa célérité v. La hauteur de la houle est caractérisée par son
amplitude a. On désigne par h la hauteur de crète à crète de la houle.
1. Quelle est la relation entre a et h ?
h = 2 a.
2. Est-ce que la houle est une onde transversale ou longitudinale ?
La déformation est verticale et la direction de propagation horizontale : onde transversale.
3. Quelle est la relation entre l, v et T ?
l = v T.
4. Comment peut-on évaluer expérimentalement la période T de la houle ?
Il
est possible de simuler la houle au laboratoire de physique avec une
cuve à ondes en utilisant une lame vibrante qui crée à la surface de
l'eau une onde progressive sinusoïdale de fréquence f =1 / T= 23 Hz. On
réalise une photographie du phénomène observé.
5. Comment peut -on évaluer la longueur d'onde l ?
Distance entre deux crètes successives.
6. Schématiser l'onde et porter sur le schéma les grandeurs l, a et h.
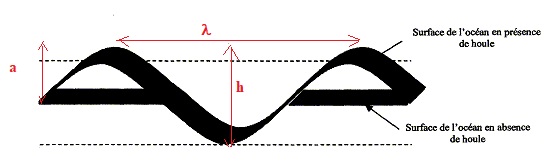
Un promeneur constate que l'eau vient battre un rocher toutes les 10 s
; deux embarcations, proches l'une de l'autre et distantes de 300 m,
oscillent verticalement en même temps en raison de la houle. Entre les
bateaux en position haute, il n'y a aucune autre crête de la houle.
7. A quelle viresse la houle se propage t-ellle ?
l = 300 m , T = 10 s ; v = 300 / 10 = 30 m /s.
La houle naît sous l'influence du vent, mais se propage calmement à la
surface de l'eau, loin de la zone où souffle le vent. La célérité des
ondes à la surface est fonction de la profondeur H d'eau libre : v =
(gH)½ avec g = 9,8 S.I.
8. Quelle est l'unité de g ?
Accélération en m s-2.
9. Estimer la hauteur H de l'eau libre.
H = v2 / g = 302 /9,8 ~92 m.
Le pacifique a une profondeur moyenne H = 5000 m.
10. Calculer la célérité des ondes ( vagues) à sa surface.
v =(9,8 x5000)½ =221,36 ~221 m /s.
11. Pour une
période moyenne T de 15 minutes ( période caractéristique d'un
tsunami ), calculer la longueur d'onde correspondante.
T = 15 x60 = 900 s.
l = v T = 221,36 x900 ~2,0 105 m ~200 km.
12. Expliquer pourquoi un navire ne peut pas apercevoir au large le passage d'un tsunami.
La distance entre deux crêtes successives est de 200 km, distance considérable par rapport à la taille du navire.
13. A mesure que la vague se rapproche de la côte, la vitesse de l'onde augmente-telle ou diminue -t-elle ?
Si la relation v =
(gH)½ reste valable en eau peu profonde : H diminue à l'approche de la côte ; la vitesse diminue.
14. Pourquoi une vague brise-t-elle ou déferle-telle aux abords d'un rivage ?
Le pied de la vague heurte le fond ; la partie supérieure bascule.
|
Force de Laplace. Induction électromagnétique.
Considèrons
deux conducteurs parallèles formant un rail de Laplace sur lequel peut
se déplacer une barre mobile conductrice MN selon le schéma suivant (
vue de dessus). Le générateur a une fem E = 5 V et une résistance
interne R = 5 ohms.
La barre MN de longueur totale L = 0,12 m a une résistance négligeable.
elle créé un court-circuit en refermant le circuit entre les deux
rails. On place MN dans l'entrefer d'un aimant en U ( largeur d =
4 cm ) où règne un champ magnétique uniforme de norme B = 0,1 S.I.
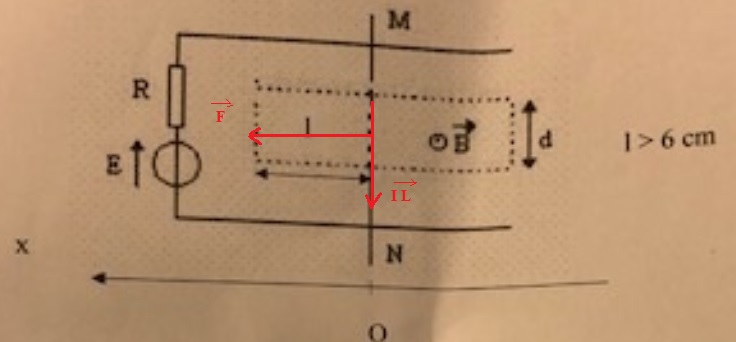
1. Quelle est l'unité du champ magnétique ?
Le tesla ( T).
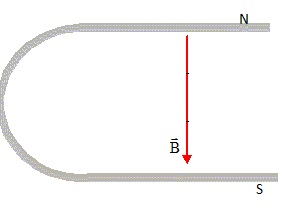
2. Schématiser un
aimant en U en précisant lepôles nord et sud et indiquer la direction
et le sens du champ magnétique dans l'entrefer.
3. Déterminer le sens et l'intensité du courant dans le circuit.
Ce sens sera pris comme sens positif et d'orienter le vecteur surface S.
Sens du courant de M vers N.
I = E / R = 5 / 5 = 1 A.
4. Déterminer la direction, le sens ainsi que la norme de la force de Laplace sur la barre MN. Voir ci-dessus.
F = I d B = 1 x 0,04 x0,1 =4 10-3 N.
5. A l'instant
initial, la barre MN est placée à la position repérée par le point O
sur l'axe des abscisses ( x =0=. Exprimer le flux magnétique F en fonction de B, l et d.
F = B l d.
La barre MN se déplace à vitesse constante dans le champ magnétique sur
une longueur de 6 cm dans le sens impliqué par la force de
Laplace.
6. Déterminer le travail exercé lors de ce déplacement de la barre MN.
W = F l = 4 10-3 x0,06 = 2,4 10-4 J.
7. Déterminer la variation de flux DF coupé par la barre.
DF=B l d = 0,1 x0,06 x 0,04 =2,4 10-4 weber.
8. Quelle est la force électromotrice induite dans le circuit si le parcours a lieu en 1 ms.
e = -DF / Dt = -2,4 10-4 / 10-3 = -0,24 V.
9. Représenter cette force électromotrice e.
e est dirigé de N vers M, elle crée un courant induit de sens contraire au courant I.
10. En conclusion, commenter le sens de la force électromotrice induite et les conséquences de son action dans le circuit.
Par ces effets électromagnétiques, le courant
induit, s'oppose à la cause qui lui donne naissance, à savoir
déplacement de MN. ( loi de Lenz).
|
|
|