Mathématiques, QCM, Caplp maths sciences 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Préciser si chacune des propositions suivantes est vraie ou fausse en justifiant.  1. Soit (un) la suite de nombres réels telle que u0 = 1 et pour tout entier naturel n, un+1 = (2+un)½. Proposition : pour tout entier naturel n, 0 < un < 2. Initialisation : u0 = 1, la propriété est vraie au rang zéro. Hérédité ; la propriété est supposée vraie au rang n, ainsi 0 < un < 2. 0+2 < un+2 < 2 +2 ; 2½ < (un+2)½ < 2 , la fonction racine carrée étant strictement croissante. Conclusion : la proposition est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel. 2½ <  un+1  < 2 , soit 0 <  un+1  < 2. La proposition est vraie. 2. Soit (un) une suite réelle positive décroissante. Proposition : la suite (un) converge vers zéro. Faux. Une suite positive décroissante et minorée  par zéro converge vers zéro.  Contre exemple : la suite définie par un+1 = 3-10 / (un+4) et  u0 = 5 et décroissante et converge vers 1. 3. Proposition :  pour tout entier naturel n non nul : 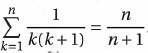Initialisation : pour n = 2 : 1 / 2 + 1 / 6  =4 / 6 = 2 / 3. , la propriété est vraie au rang 2. Hérédité ; la propriété est supposée vraie au rang n. Pour k = n+1 : n / (n+1) + 1/ [(n+1)(n+2)]=n(n+2)+1) / [(n+1)(n+2)]=(n2+2n+1) / [(n+1)(n+2)]=(n+1) / (n+2). La propriété est donc vraie au rang n+1. Conclusion : la proposition est vraie au rang 2 et héréditaire, elle est donc vraie pour tout entier naturel non nul. La proposition est vraie. 4. Soit (un) la suite de nombres rels telle que u0 = 1 et, pour tout entier naturel, un+1 = un + e-un. Proposition :  cette suite diverge vers  plus l'infini. Vrai. un+1 - un = e-un >0, la suite est positive et croissante. un+1 / un =1+ 1/ (uneun) > 1, alors la suite (un) diverge. 5. Soit une fonction définie et dérivable sur un intervalle I. Proposition :  Si f est strictement croissante sur I, alors f ' est strictement positive sur I. Faux. Contre exemple : la fonction f(x) = x3 est strictement croissante, bien que sa dérivée s'annule en zéro. 6. Proposition : pour tout réel x, ex > 1+x. Vrai. f(x) = ex-x-1 ; f '(x) = ex-1. f '(x) > 0 si x >0 , f(x) croissante de zéro à plus l'infini. f '(x) < 0 si x < 0 , f(x) décroissante de plus l'infini à zéro. f(x) >0, donc pour tout réel x, ex > 1+x. ex est strictement positif. 7. Soit f la fonction définie sur R par f(x) = sin (x) / x pour x différent de zéro et f(x) = 1 si x = 0. Proposition : la fonction f est dérivable sur R. Vrai. f(x) = sin (x) * (1 /x) est dérivable sur R-{0} en tant que produit de fonctions dérivables. Développement limité de sin(x) à l'ordre 1 au voisinage de zéro : sin(x) = x+o(xn). (f(x) - f(0)) /  (x-0) = 0. Au voinage de zéro, la dérivée à droite et à gauche sont égales. 8. Soit f une solution sur R de l'équation différentielle y" +3y' +2y = 0. Proposition : la limite  en plus l'infini de f(x) est égale à zéro. Vrai. Equation caractéristique : r2 +3r+2=0 ; discriminant D =32-4*2=1. solutions : r1 =  (-3+1) / 2 = -1 et r2 = (-3-1) / 2 = -2. f(x) = A e-2x +Be-x avec A et B deux constantes réelles. En plus l'infini, e-2x et e-x tendent vers zéro. 9. Pour tout réel x, on note D(x) le déterminant de la matrice 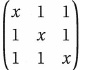Proposition : D(x) est nul si et seulement si x = 1. Vrai. D(x) = x3 +1+1-x-x-x=x3-3x+2. 10. On lance 6 fois un dé équilibré ( six faces équiprobables numérotées de 1 à 6 ). Proposition : la probabilité d'obtenir exactement une fois la face "6" est égale à 5 / 6. Faux. Soit X la variable aléatoire égale au nombre de fois que l'on obtient la face "6". X suit la loi binomiale de paramètres n = 5 et p = 1 /6. p(X=1) ~0,40. .... 11. Soit n un entier naturel non nul et x1....xn des réels. On note m la moyenne de la série statistique ( x1 ... xn) et s son écart type. Pour tout i appartenant à [1 ; n], on pose yi = 2xi+3. Proposition : la série statistique  (y1 ...yn) a pour moyenne 2m+3 et pour écart type 2s+3. Faux.   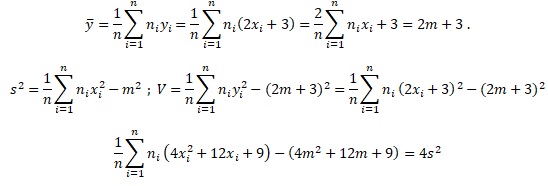12. Soit X une variable aléatoire qui suit la loi exponentielle de paramètre 0,5. Proposition : la probabilité de l'événement (X < ln(9)) est égale à 1 / 3. Faux. P(X < ln(9))= 1-exp(-0,5 ln(9)) =1-exp(-ln(3)) =1-exp(ln(1 /3)) = 1-1/3 = 2 /3. 13. Dans le plan complexe, on considère les points A, B, C et D d'affixes 1 , i, -1, -i. On note G le cercle unité, c'est à dire l'ensemble des points dont l'affixe vérifie |z| =1. Si M est un point du cercle, on note p(M) le produit des distances de M aux points A, B, C et D : p(M) = MA x MB x MC x MD. Proposition : Lorsque M décrit le cercle, le maximum de p(M) est égal à 2. Vrai. M (x ; y) tel que x2 +y2 = 1. MA = [(1-x)2 +y2]½ = [ 1-2x+x2 +y2]½ =(2-2x)½ ; MB = [(0-x)2 +(y-1)2]½ =[ 1-2y+y2 +x2]½ =(2-2y)½ ; MC = [(-1-x)2 +y2]½ =[ 1+2x+x2 +y2]½ =(2+2x)½ ; MD = [(0-x)2 +(-1-y)2]½ =[ 1+2y+y2 +x2]½ =(2+2y)½ ; p(M) =4[(1-x)(1+x)(1-y)(1+y)]½ =4[(1-x2)(1-y2)]½ =4[(1-x2)x2]½ =4x(1-x2)½. On pose f(x) = 4x(1-x2)½. Calcul de f '(x) : u = 4x ; v = (1-x2)½ ; u' = 4 ; v' = -x (1-x2)-½ ; u'v + v'u = 4 (1-x2)½ -4x2(1-x2)-½ =4[(1-x2)-x2] / (1-x2)-½ =(1-2x2) / (1-x2)-½ = f '(x) >0  si x < 2-½ et f(x) croissante. f '(x) <0  si x > 2-½ et f(x) décroissante. f '(x) = 0 si x = 2-½ et f(x) possède un maximum égal à 2. 14. Dans le plan euclidien rapporté à un repère orthonormé, soit A(1 ; 0) et B(0 ; 1). Proposition : L'ensemble des points M du plan tels que MA = 2½MB est un cercle de rayon 2. Vrai. M(x ; y) : MA2 = (1-x)2 +y2 ; MB2 = (1-y)2 +x2 ; (1-x)2 +y2 = 2[(1-y)2 +x2 ]. 1+x2-2x+y2=2(1-2y+y2+x2). 0=1+x2+2x-4y+y2. 0=(x+1)2 +(y-2)2 -4. (x+1)2 +(y-2)2 = 4 = 22. Cercle de centre (-1 ; 2) et de rayon 2. 15. Dans l'espace affine muni d'un repère orthonormé, on considère la sphère S d'équation x2 +y2 +z2 +6x-2y-15=0 et le plan P d'équation 2x-2y+z-4=0. Proposition : l'intersection de S et de P est un cercle de rayon 3. Faux. x2 +y2 +z2 +6x-2y-15=2x-2y+z-4. x2 +4x+y2 +z2 -z-11=0. (x+2)2-4+y2 +(z-0,5)2-0,25-11=0. (x+2)2+y2 +(z-0,5)2=15,25 Cercle de centre (-2 ; 0 ; 0,5) et de rayon 15,25½.