Lunette de Galilée,
fibre optique,
Caplp maths sciences 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Partie
D1 : Comment peut-on améliorer sa vision ?
51. Énoncer
le principe de Fermat pour l’optique géométrique.
La lumière se propage d'un point à un autre de façon à limiter son
temps de trajet.
52. En déduire le
mode de propagation des rayons lumineux dans les milieux homogènes.
Dans un milieu homogène la lumière se propage en ligne droite.
Dans le cadre de son enseignement sur le module HS4 en première
baccalauréat professionnel, un enseignant propose l’activité de
synthèse qui se trouve dans le document 3.1 et qui sera évaluée avec la
grille nationale (document 2.2).
Madame
Jivoiflou porte des lunettes avec le même verre à gauche et à
droite. Malheureusement sur le trajet du chantier, lors d'un petit choc
en voiture, ses lunettes se sont cassées. Vous récupérer un morcceau de
verre et vous devez déterminer sa vergence afin de pouvoir lui acheter
une paire de lunettes de substitution dans une pharmacie.
Problématique : comment déterminer exprimentalement la distance focale du verre ?
1. Vous disposez sur la table d'une lentille identique à celle du verre de madame Jivoiflou.
a. S'agit-il d'une lentille convergente ou d'une lentille divergente ? Argumenter.
Observer au toucher les deux faces de la lentille : elles sont bombées au centre ( convexes ), la lentille est convergente.
b. Proposer un protocole expérimental simple ( sans matériel) prmettant d'évaluer la distance focale de cette lentille.
Former l'image nette sur
la table d'un tube néon allumé fixé au plafond. Pour cela on déplace la
lentille. Le néon pouvant être considéré à l'infini, la distance
lentille-image ( table) est égale à la distance focaale cherchée. On trouve f ' ~ 19 cm.
La vergne ce vaut 1 / 0,19 ~5,3 dioptries.
2. Proposer un
protocole expérimental et un schéma annoté permettant de déterminer
précisément la distance focale de la lentille. En déduire la vergence.
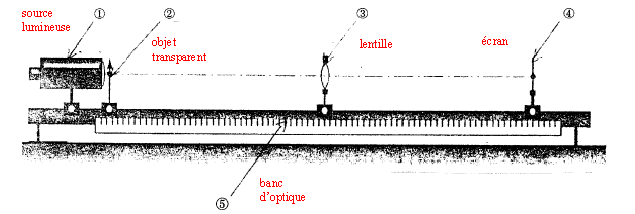
Placer la lentille à environ 1,5 m de l'objet. Déplacer l'écran pour former une image nette.
Distance lentille écran = f' ' = 20 cm ; vergence : 1 / 0,20 = 5 dioptries.
53. En se basant
sur la seule partie A du document 3.1, compléter le document réponse
3 en remplissant la liste des capacités à évaluer ainsi que les
numéros des questions relevant de la compétence Réaliser.
Choisir un protocole expérimental, l'exécuter, expérimenter.
55. En utilisant la méthode son choix, répondre à la question 2 de la
partie B.
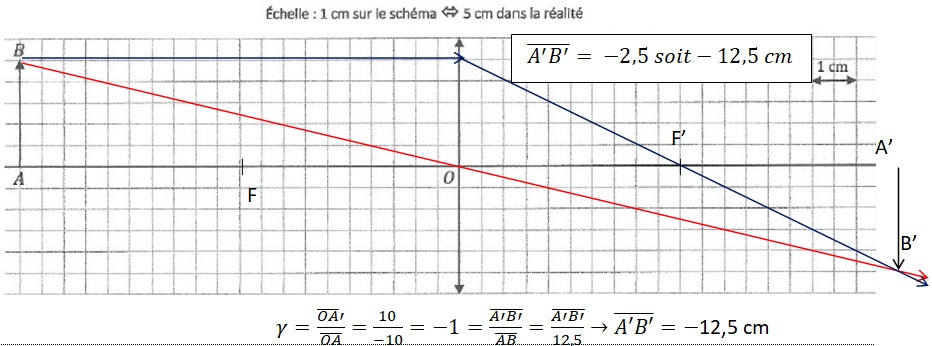
Le schéma ci-dessous utilise une lentille de même vergence que dans la partie A.
Placer les foyers F et F' puis construire l'image A'B' de AB.
56. Cet exercice peut-il être utilisé pour une évaluation certificative
? Justifier la réponse.
Partie D2 : Étude de la
lunette de Galilée.
Afin de pouvoir surveiller le chantier à distance, Madame Jivoiflou
achète une paire de jumelles de théâtre constituée de deux lunettes de Galilée identiques,
d'axes optiques parallèles, dont le fonctionnement est donné.
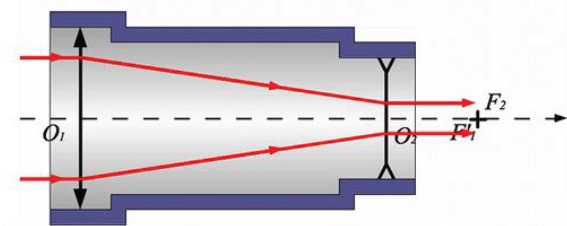
Nous n’étudierons dans la suite qu’une seule jumelle constituée d’un
objectif et d’un oculaire.
Les caractéristiques sont les suivantes :
L'objectif est constitué d'une lentille L1 de focale image f '1= 0,20 m.
L'oculaire est constitué d'une lentille L2 de focale image f '2 = −20 mm.
On observe un objet AB de hauteur h = 0,60 m situé à la distance D
= 200 m dont A est sur l’axe optique et B dans une direction perpendiculaire.
Une molette de réglage permet de déplacer l’oculaire par rapport à
l’objectif.
L’oculaire est placé tel que O1O2= 0,17 m.
La notice indique un grossissement de 10.
L'oeil de l’observateur est supposé emmétrope.
Dans cette partie, on considérera que les axes optiques des deux
lentilles sont confondus et orientés positivement vers l’oeil, et on négligera l’épaisseur des
lentilles (lentilles dites minces).
57. Préciser si les lentilles utilisées pour l’objectif et pour
l’oculaire sont convergentes ou divergentes.
L1, objectif convergent.
L2 : oculaire divergent.
58. Les lentilles sont utilisées dans les conditions de l’approximation
de Gauss. Quelles sont ces conditions ?
Les rayons lumineux issus de l'objet sont peu inclinés par rapport à
l'axe optique et peu éloignés de cet axe ( rayons paraxiaux).
59. Les lentilles sont traitées pour limiter les aberrations
chromatiques de l’image.
À quoi sont dues ces aberrations chromatiques ?
L'indice de réfraction du matériau composant les lentilles varie
en fonction de la longueur d'onde de la lumière. Matériau dispersif.
60. Déterminer la position de l’image A’ de A donnée par la seule
lentille L1. On pourra par exemple calculer O1A’. Ce résultat était-il prévisible ?
61. Cette image est-elle réelle ou virtuelle ?
L'objet étant considéré à l'infini, l'image se forme au foyer image de la lentille L1.
O1A’=0,20 m.
62. Calculer la taille de l’image A’B’. L’image est-elle droite ou
renversée ?
L'image est renversée : |g| = 0,20 / 200 =1,0 10-3.
Taille de A'B' : 0,001 h = 0,001 x0,60 = 6,0 10-4 m.
63. L’image précédente sert d’objet pour la deuxième lentille.
Construire l’image A’B’ de AB par la lentille L1 puis l’image A’’B’’ de A’B’ par la lentille L2 .
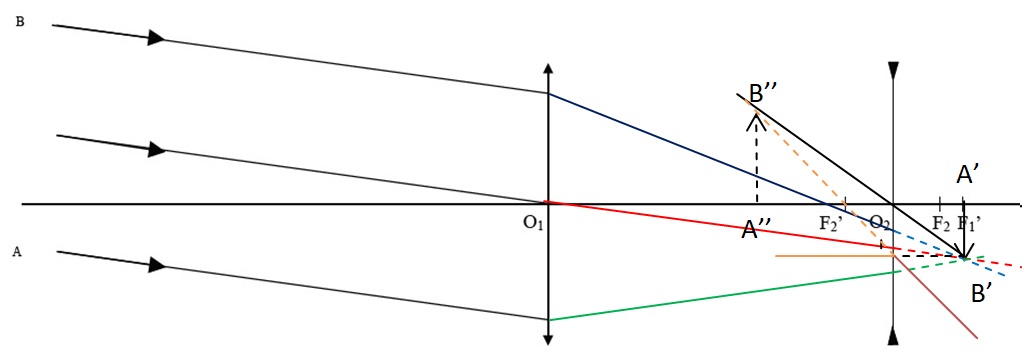
|
|
....
|
64.
Déterminer par le calcul la position de l’image A’’ de A’ donnée par la
lentille L2. On pourra, par exemple, donner la distance algébrique
O2A’’. L’image est-elle réelle ou virtuelle pour l’ensemble de la
lunette ?
L'image est virtuelle et droite pour l'ensemble de la lunette.
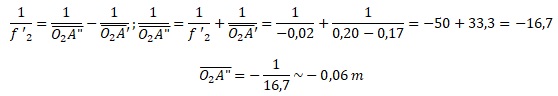
65. Sachant que l’oeil est situé à 1,5 cm de l’oculaire,
l’image est-elle nette pour l’observateur avec ce réglage ?
Distance oeil - objet A"B" = 6 +1,5 cm = 7,5 cm, inférieure à la
distance minimale de vision distincte ( 25 cm). L'image est floue sur
la rétine.
66.
Calculer la taille de l’image A’’B’’. Dans quel sens est-elle ?
A"B" / A'B' = O2A" / O2A'.
A"B" = O2A" x A'B'/ O2A'.
A"B" =0,06 x 6,0 10-4 / 0,03 =1,2 10-3 m = 1,3 mm.
67. La
molette sur la jumelle permet de déplacer la lentille L2 (oculaire) par
rapport à la lentille L1 (objectif). Où faut-il placer O2 pour avoir
une image A’’B’’ rejetée à l’infini ? On pourra, par exemple, donner la
nouvelle distance algébrique O1O2.
A'B' doit se trouver en F2, foyer objet de l'oculaire. F '1 et F2 confondus.
Nouvelle distance O1O2 : 18 cm.
68. Pourquoi parle-t-on de système
afocal dans ce cas ? Préciser l’avantage d’un tel système pour l’oeil.
Des rayons parallèles avant l'entrée du système ressortent parallèles du système.
L'image d'un objet situé à l'infini est rejetée à l'infini. L'oeil observe sans accommoder, sans fatigue.
69. Donner l’expression algébrique du grossissement G de ces jumelles
en fonction de f '1 et f '2. Le calculer. Le résultat est-il
conforme aux données de la notice ?
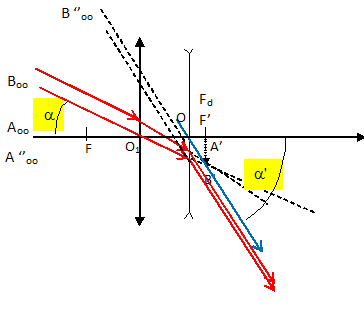
Les angles étant petits on assimile la tangente à l'angle exprimé
en radian.
G = a'/a avec a' = A'B' / OF' et a = A'B' / F'O1.
G = F'O1 /OF' =20 / 2 = 10, valeur conforme à la notice..
Partie E : Raccordement du chantier
à la fibre optique.
En application de la loi du 6 août 2015 pour la
croissance, l’activité et l’égalité des chances économiques, le
raccordement à la fibre optique devient obligatoire lorsque des travaux
sont réalisés en logements collectifs ou dans un édifice accueillant
des locaux professionnels. Une entreprise réalise donc le câblage du
chantier avec une fibre optique longue de 4 km.
Partie E1 : comment
fonctionne une fibre optique ?
70. Lors d’une séance de cours, un
élève, pose à son
professeur les deux questions suivantes :
- Qu’est-ce que le principe
de réflexion et de réfraction de la lumière ?
- Pourquoi le rayon
est-il totalement réfléchi et n'est plus du tout réfracté ?
Proposer
une réponse à chacune de ces deux questions.
Lorsque la lumière change de milieu de propagation, elle peut subir :
un retour dans le milieu initial, avec une direction différente, c'est la réflexion.
Un changement de direction dans le nouveau milieu, c'est la réfraction.
La réflexion totale se produit lorsque la lumière passe d'un milieu à
un autre milieu d'indice plus faible et quand l'angle d'incidence
dépasse une valeur limite.
71. En utilisant le
document 1.8, calculer la valeur minimale de l’angle i1 permettant
d’avoir une réflexion totale en A.
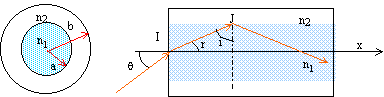
Un rayon laser se propageant dans
l'air dans un plan contenant l'axe de la fibre
pénètre dans le coeur de la fibre. Le rayon
incident au point I reste dans le coeur si l'angle
qi
d'incidence à l'entrée de la fibre est
inférieur à un angle a
que l'on va calculer :
en I, dioptre air/coeur :
nair sin qi
= n1 sin r ; sin qi
= n1 sin r
(1)
en J, il y a réflexion
totale : dioptre coeur/gaine : n1 sin i =
n2 sin 90 = n2 ; sin i = n2
/n1 = 1,45 / 1,47 = 0,986 ; i = 80,5° ;
les angle i et r sont
complémentaires soit : sin r = cos i = cos 80,5 =
0,164 ;
de plus
(1)
s'écrit : sin a
= n1 sin r = 1,47*0,0,164
=0,2416
; a ~ 14°.
72. On définit l’ouverture numérique
de la fibre optique, qui caractérise le cône d’acceptance de la fibre,
par ON = sin (a). Montrer que ON=(n12− n22)½ et calculer sa valeur.
(1)
s'écrit : sin a
= n1 sin r ; en J, il y a réflexion totale
: sin i = n2 /n1 et sin r = cos
i.
sin2 i = (n2
/n1)2 ; cos2 i
=1-sin2 i =1-(n2
/n1)2 =
(n12-n22) /
n12.
cos i =sin r =
(n12-n22)½
/ n1 ; or sin a
= n1 sin r =
(n12-n22)½.
ON = (1,472− 1,452)½ =0,242.
73. Calculer la vitesse
de propagation de la lumière dans le coeur de la fibre d’indice n1 = 1,47. En déduire le temps mis par la lumière pour arriver au bout de la
fibre dans le cas où i=85°.
v = 3,0 108 / 1,47 =2,04 108~2,0 108 m /s.
Distance à parcourir ; 4,0 / sin (85) =4,015 km.
Durée du parcours : 4,015 103 / ( 2,04 108) ~2,0 10-5 s.
Partie E2 : Atténuation dans la fibre optique.
La lumière utilisée pour transmettre les informations est un laser de
longueur d’onde l = 800 nm.
75. En utilisant le graphe du 3°) du document 1.9, déterminer le
coefficient d’atténuation correspondant à ce laser.
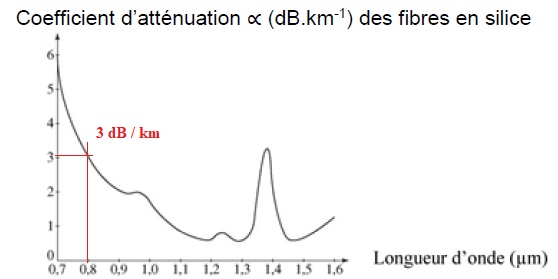
76. Calculer le rapport P0 / P1.
Atténuation A (dB)=10 log (P0 / P1) avec A / L = 3 dB / km soit A = 12 dB.
log (P0 / P1)= 1,2 ; P0 / P1~15,8 ~16.
77. En déduire si les signaux qui arrivent sur le chantier sont
exploitables.
P1 = P0/ 16 ~0,063 P0, valeur supérieure à 0,01 P0 : les signaux sont donc exploitables.
|
|