Groupe électrogène;
cycle moteur, acoustique,
Caplp maths sciences 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Partie A1 : Étude électrique d’un ballon éclairant.
Lors d’un chantier de nuit, ou l’hiver, il faut prévoir un éclairage suffisamment efficace pour pouvoir travailler dans les meilleures conditions possibles. Un ballon éclairant, alimenté par un groupe électrogène, permet la diffusion d’une lumière douce et puissante.
1. Rappeler la relation entre puissance électrique P, énergie E et durée Dt. Préciser les unités.
E (J) = P(W) Dt (s).
E (kWh) = P(kW) Dt (h).
2. Rappeler la relation entre puissance électrique P, tension U, intensité du courant I et facteur de puissance cos f en régime sinusoïdal. Préciser les unités. Combien vaut cos f dans le cas d’une lampe ?
P(W) = U(V) I(A) cos f.
Dans le cas d'une lampe cos f = 1.
3. Le groupe électrogène délivre une tension identique à celle du réseau, U = 230 V, et alimente une des lampes du ballon de puissance P= 1 000 W. Calculer l’intensité I du courant électrique qui traverse cette lampe.
I = P / U = 1000 / 230 ~4,35 A.
4. Quelles sont les précautions à prendre du point de vue du risque électrique lors de l’utilisation d’un groupe électrogène ?
Interconnecter toutes les masses.
Protéger chaque canalisation du groupe avec un dispositif différentiel ( I < 30 mA).
Partie A2 : Étude du moteur du groupe électrogène.
On considère le cycle d’un moteur thermique idéal.
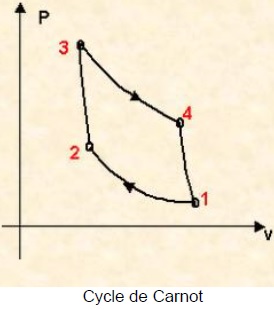
On considère que le fluide mis en jeu obéit à la loi des gaz parfaits.
- Une compression isotherme à Tf (température de la source
froide) correspond au passage des étapes 1 à 2 et une détente isotherme
à Tc (température de la source chaude) au passage des étapes 3 à
4. Dans ces deux cas-ci : PV = constante.
-
Une compression adiabatique correspond au passage des étapes 2 à 3 et
une détente adiabatique au passage des étapes 4 à 1. Dans ces deux
cas-là, PVg= constante
5. Exprimer les
travaux et les chaleurs reçus par le moteur et ses variations d’énergie
interne lors des deux transformations isothermes en fonction de
variables d'état de son choix (par exemple, les volumes et les
températures aux points 1, 2, 3 et 4). Préciser le signe de chaque
grandeur.
La température étant constante, la variation d'énergie interne est nulle
DU = Q + W =0 soit Q = -W.
Travail élémentaire des forces de pression dW = -PdV.
P = nRT / V ; dW = -nRT dV / V = -nRT d ln(V).
W1 -->2 = nRTf ln(V1 / V2) > 0.
Q 1 -->2 = nRTf ln(V2 / V1) < 0.
W 3 -->4 = nRTc ln(V3 / V4) < 0.
Q 3 -->4 = -nRTc ln(V4 / V3) > 0.
6. Lors des deux transformations adiabatiques en fonction de variables d'état de son choix (par
exemple, les seules températures Tf, température de la source froide, et Tc, température de la source chaude). Préciser le signe de chaque grandeur.
Transformation adiabatiques Q = 0.
Travail élémentaire des forces de pression dW = -PdV.
PVg = Cste ; dW = -cste /Vg dV.
Intégrer entre les états 2 et 3 :
W23 = -Cste / (1-g) [V1-g]2 3 =Cste / (g-1) (V31-g -V21-g) < 0.
W41 = Cste / (g-1) (V11-g -V41-g) > 0.
7. En déduire, pour l’ensemble du cycle, la chaleur totale reçue Qcycle et le travail total reçu Wcycle en fonction de variables d'état imposées cette fois : les quatre volumes et les deux températures Tc et Tf.
On peut remarquer, en le justifiant, que W23 + W41= 0.
Cste = P3V3g =P2V2g .
W23 =(P3V3 -P2V2 )/ (g-1)= nR(T3-T2) / (g-1) = nR ((Tc-Tf) / (g-1).
De même : W41 =(P4V4 -P1V1 )/ (g-1)= nR(Tf -Tc) / (g-1).
W23 + W41= 0.
Wcycle = W1 -->2 +W 3 -->4 =nRTf ln(V1 / V2) +nRTc ln(V3 / V4).
Qcycle =nRTf ln(V2 / V1) +nRTc ln(V4 / V3) .
8. Définir le rendement thermodynamique d’un moteur et montrer que celui du cycle de Carnot peut s’écrire :
h= 1- Tf ln(V1/V2) / (Tc ln(V4/V3)).
Rendement : travail fourni / énergie dépensée ( source chaude).
h= Wcycle / Q 3 -->4 =[Tf ln(V2 / V1) +Tc ln(V4 / V3)] / [Tc ln(V4 / V3) ].
h= [-Tf ln(V1 / V2) +Tc ln(V4 / V3)] / [Tc ln(V4 / V3) ].
h=1- Tf ln(V1/V2) / (Tc ln(V4/V3)).
9. Lors des transformations adiabatiques, montrer que l’on peut écrire la loi de Laplace sous une autre forme,
T1/(g-1) V = constante.
En déduire l’expression de h en fonction uniquement de Tf et de Tc.
PVg = Cste et PV = nRT.
nRT / Vx Vg = Cste ; T V g-1 = autre constante ; T1/(g-1) V = constante.
V2 T21/(g-1) =V3 T31/(g-1) ; V1 T11/(g-1) =V4 T41/(g-1) ;
V2 Tf1/(g-1) =V3 Tc1/(g-1) ; V1 Tf1/(g-1) =V4 Tc1/(g-1) .
V1/V2= V4 / V3.
h=1- Tf / Tc.
10. Calculer ce rendement si Tf = 300 K et Tc = 2500 K.
h=1-300/2500 =0,88.
|
|
....
|
Un extrait
du site internet du constructeur du groupe électrogène est reproduit
ci-après : « Le groupe électrogène délivre au maximum 5500 W et est
alimenté par un moteur à essence de 9,55 kW. Lorsque le groupe
électrogène est utilisé à 2/3 de sa puissance nominale (ce qui donne
3 667 W ), le moteur consomme 2,5 L de carburant à l'heure et, compte
tenu des pertes thermiques inévitables dans les moteurs à combustion
interne, il en résulte un rendement global énergie électrique délivrée /
énergie fournie par le carburant n'excédant pas 17 %. ». 11. On fait
l’hypothèse que le groupe électrogène décrit ci-dessus fonctionne
suivant un cycle de Carnot. On prendra pour cela les valeurs numériques
des températures de la question 10., un taux de compression V1/V2=7, la pression au point 1 P1 = 105 Pa et g= 1,40.
Calculer les pressions aux points 2 et 3. Conclure quant
à la vraisemblance de ce modèle.
P1V1 = P2V2 ; P2 =P1V1 / V2=7 105 Pa.
P2V2g=P3V3g ; P3 = P2(V2/V3)g.
De plus
Tf1/(g-1) V2 =
Tc1/(g-1) V3 ; V2 / V3 =(Tc / Tf)1/(g-1) =(2500/300)0,4=2,335.
P3 =7 105 x 2,335 ~ 1,63 106 Pa.
Le cycle de Carnot correspond à des transformations réversibles, ce n'est pas le cas dans un groupe électrogène.
On donne : doctane =0,703 ; M(octane) =12 x8 +18 = 114 g / mol.
12. En considérant que le
carburant est formé uniquement d’octane, calculer la quantité de
matière de carburant correspondant à une consommation d’une heure du
moteur du groupe électrogène fonctionnant à 2/3 de sa puissance
nominale.
2,5 L correspond à 2,5 x 0,703 ~1,76 103 g.
noctane = n = 1,76 103 / 114 ~15,4 mol.
13. Écrire la réaction de combustion complète de l’octane.
C8H18 (g)+ 12,5O2 (g)--> 8CO2 (g)+ 9H2O(g).
On
donne : DH°f 298 (octane gazeux) = −208,52 kJ / mol ; DH°f 298 (dioxygène gazeux)= 0 kJ / mol ;
DH°f 298 (CO2 gazeux)=
−393,52 kJ / mol ; DH°f 298 (eau gaz)=−241,8 kJ / mol.
14. En déduire l’enthalpie standard molaire de
combustion totale de l’octane.
DH°r= 8 DH°f 298 (CO2 gazeux) +9DH°f 298 (eau gaz) -DH°f 298 (octane gazeux).
DH°r=8(-393,52) +9(-241,8)-(-208,52)= -5,14 104 kJ / mol.
15. En déduire l’énergie libérée par la
combustion du carburant en une heure.
5,14 103 x15,4 =7,92 104 kJ.
16. Calculer le travail
électrique fourni par le groupe électrogène fonctionnant à 2/3 de sa
puissance nominale en une heure.
3667 x 3600 =1,32 107 J = 1,32 104 kJ.
17. Calculer le rendement global du
groupe électrogène. Commenter cette valeur par rapport à celle annoncée
par constructeur du groupe électrogène.
1,32 104 / (7,92 104) ~0,167 ( 16,7 %) en accord avec le constructeur.
Partie A3 : Étude acoustique du groupe électrogène.
Les résultats donnés par le constructeur concernant le niveau
d’intensité sonore correspondent à une mesure à 7 m de l’appareil. Si
un ouvrier doit être plus près du groupe électrogène, il faut en tenir
compte.
18. Donner la relation entre le niveau d’intensité sonore L, l’intensité sonore I et l’intensité sonore de référence I0. Préciser les unités.
L = 10 log (I / I0).
L en décibel ( dB) et I en W m-2.
19. Donner la
relation entre l’intensité sonore I, la puissance acoustique P et la
surface S parcourue par l’onde sonore. Préciser les unités.
I = P/ S.
I en W m-2 ; P en W et S en m2.
20. Un groupe
électrogène est décrit par le fabricant comme silencieux avec un niveau
d’intensité sonore de 54 dB à 7 m. Calculer son niveau d’intensité
sonore à 1 m du groupe électrogène ainsi qu’à 50 m, distance des
premières habitations. Conclure sur les
précautions à prendre pour son utilisation.
A 7 m : I = I0 100,1 L =10-12 x 105,4 =2,51 10-7 W m-2.
P= (4pd2)I=4 x3,14 x72 x2,51 10-7 =1,55 10-4 W.
A 1 m : I = 1,55 10-4 /(4 x3,14) =1,23 10-5 W m-2.
L = 10 log(1,23 10-5 / 10-12) ~71 dB.
Des protections auditives sont nécessaires.
A 50 m : I = 1,55 10-4 /(4 x3,14x502) =4,93 10-9 W m-2.
L = 10 log(4,93 10-9 / 10-12) ~37 dB.
|
|
