Expériences
historiques en physique : Galilée, Young, Joule, Hertz.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Galilée
et la chute des corps.
Dans
toute cette première partie, le référentiel terrestre est supposé
galiléen. On note t la variable associée au temps et g l’intensité du
champ de pesanteur terrestre (on prend g≈10 m.s−2 et on
considère ce champ uniforme). On néglige également l’effet de la
poussée d’Archimède.
Pour Aristote, la vitesse de chute d’un mobile est proportionnelle à
son poids.
Cependant, Galilée proposa l’expérience de pensée suivante : […].
Considérons deux masses m1 et m2< m1
en chute libre. D’après Aristote, la masse m1 atteint le sol
avant la masse m2. En reliant, à l’aide d’un fil, les masses
m1 et m2, on obtient alors un système (S) plus
lourd que la masse m1 seule et donc a priori plus rapide
pendant sa chute. Cependant ce système (S) est ralenti par la masse m2
(m2 plus lente faisant l’effet « d’un parachute »). (S) est
donc plus lent que la masse m1
seule alors qu’il est plus lourd, il y a donc un paradoxe…. Étienne
Klein, extrait d’une conférence intitulée « De quoi l’énergie est-elle
le nom ? »
En 1602, Galilée a l’intuition que le mouvement de chute libre
(c’est-à-dire sans frottement) d’un corps dans le champ de pesanteur
terrestre est indépendant de la masse de ce corps. Mais il se heurte à
l’impossibilité de mesurer précisément la vitesse d’un corps tombant à
la verticale. Galilée entreprit alors d’étudier le mouvement de chute
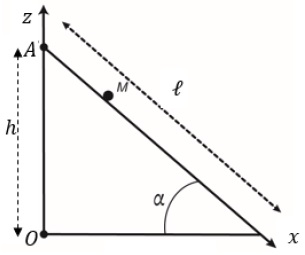
de corps à l’aide d’un plan incliné d’un angle a
par rapport à l’horizontale. On note Oz l’axe vertical ascendant et Ax
l’axe confondu avec la ligne de plus grande pente du plan incliné. On
pose OA =h.
Ne disposant pas de chronomètres précis, Galilée fait rouler des billes
sur un plan incliné en faisant teinter des chlochettes que la bille
fera sonner en passant.. Il dispose ces chlochettes à intervalles
variables sur le plan jusqu'à obtenir un son régulier.
Le tintement est régulier lorsque les chlochettes sont placées à des
intervalles 1, 3, 5, 7...
En une unité de temps, la bille parcourt une unité de distance.
En 2 unités de
temps, la bille parcourt 3+1=4 unités de distance.
En
3 unités de temps, la bille parcourt 5+3+1=9 unités de distance.
On
souhaite étudier cette expérience de Galilée en analysant le mouvement
d’un mobile, assimilé à un point matériel de masse m repéré par le
point M, lâché sans vitesse initiale depuis le point A. On néglige tout
frottement lors de cette chute s’effectuant sur le plan incliné .
Q1. Déterminer, à
l’aide de la relation fondamentale de la dynamique, l’accélération x"
̈(t)= a du point M en fonction de g et a.
Le système est soumis à son poids et à l'action du plan.
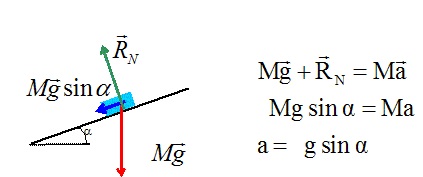
. Q2. Exprimer le temps de
chute t0 nécessaire pour parcourir, suivant la ligne de plus
grande pente, la distance ℓ en fonction de g, h et ℓ. Commenter.
La vitesse est une primitive de l'accélération et la vitesse initiale
est nulle : v(t) = g sin a
t avec sin a = h
/ l.
La position est une primitive de la vitesse et la position initiale est
l'origine de l'axe Ax.
x =½g h / l t2.
l =½g h / l t02;
t02=2l2
/ (gh) ; t0 = l
(2 /(gh))½.
Si le temps double, alors la hauteur h quadruple ; si le temps double,
la distance parcourue sur le plan incliné est multipliée par 4.
Pour un mobile partant du repos et en négligeant les frottements, la
distance parcourue est proportionnelle au carré du temps.
Q3. Un enseignant
pose la question à choix multiple suivante :
Soient deux points matériels P1 et P2 de masses
respectives m1 et m2 (m2 < m1).
On lâche ces deux masses, sans vitesse initiale, d’une hauteur h sur un
plan incliné. Quel mobile touche le sol en premier ? On néglige l’effet
des frottements. »
A) P1 ; B) P2 ; C) P1 et P2
touchent le sol en même temps.
15 élèves répondent A) et 20 répondent C).
Proposer une remédiation.
Expérience du tube de Newton dans lequel on fait le vide. Une feuille
et une bille en acier partant du repos, touchent en même temps le sol.
Expérience des trous d'Young.
Dans
toute cette partie, l'air possède les propriétés optiques assimilables
à celles du vide.
En 1801, T Young entreprend une expérience d'interférences visant à
démontrer que la lumière visible peut être décrite comme une onde
scalaire : on parle de vibration lumineuse. L'observation expérimentale
de cette figure d'interférences a permis de remettre en cause le modèle
particulaire de la lumière que Newton avait proposé au 17è siècle.
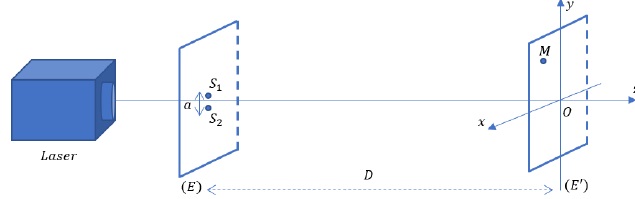
En classe, on peut facilement mettre en évidence l'interférence à deux
ondes lumineuses à l'aide du montage représenté ci-dessous. Il est
constitué :
- d'un laser émettant un faisceau lumineux cylindrique d'axe Oz. Cette
source est supposée monochromatique, de pulsation w et de longueur d'onde l0.
- d'un plan E percé de deux trous circulaires, identiques, de rayon b,
distants de a et centrés sur les points S1 ( 0 , ½a , -D et S2
( 0 , -½a ; -D). Le faisceau éclaire entièrement et de manière uniforme
ces deux trous sources.
- d'un écran de projection E' parallèle à E et situé à une distance D
de (E) telle que D >> a. ( On choisit D = 1 m, a = 0,5 mm). Un
point M quelconque de l'écran (E') est repéré par les variables ( x, y,
0). Le champ d'onservation est tel que |x| << D et |y | <<
D.
Q1. Montrer que
l'éclairement E(M)
en M est donné par : E(M)=
2 E0 [ 1 + cos (
2 p a y) / ( l0D)]
si on considère que les vibrations lumineuses au point M, issues des
deux trous source S1 et S2, sont décrites
respectivement par les
expressions s1(M, t) = S0 cos [wt-2p S1M / l0] et s2(M,
t) = S0 cos [wt-2p S2M / l0]. S0
est une constante. E0 est
l'éclairement qui serait obtenu en masquant l'un des deux trous.
Décrire la figure d'interférences.
Au point M de
l'écran :
vibration
résultante : s(M,t) =s1(M,
t) +s2(M, t)
=S0 ( cos
[wt-2p S1M / l0]+cos [wt-2p S2M / l0] ).
éclairement : E(M)=
< s(M, t)
2>
E(M)= S20
( < cos2
[wt-2p S1M / l0] > + < cos2 [wt-2p S2M / l0] )>+
< cos
[wt-2p S1M / l0].cos [wt-2p S2M / l0] > ).
<
cos2 [wt-2p S1M / l0] > = < cos2 [wt-2p S2M / l0] )>0,5.
< cos [wt-2p S1M / l0].cos [wt-2p S2M / l0] > = <
cos [2wt-2p S1M / l0+2p S2M / l0] >+ <
cos[ 2p S2M / l0-S1M / l0] >.
< cos [2wt-2p S1M / l0+2p S2M / l0] > = 0
E(M)= S20
( 1+ cos[ 2p / l0 (S2M-S1M)] ).
S1M2 =(y-½a)2 +x2 +D2.
S2M2 =(y+½a)2 +x2 +D2.
S2M2 -S1M2 =2ay.
S2M2
-S1M2 =(S2M+S1M)(S2M-S1M)
avec S2M+S1M
~2D.
S2M-S1M~ay
/ D.
E(M)= S20 [
1 + cos ( 2 p a
y) / ( l0D))]
avec S20=2 E0.
Q2.
Comparer l'éclairement calculé à la question précédente avec la figure
ci-dessous obtenue expérimentalement sur l'écran (E'). Quel autre
pphénomène optique doit-on prendre en compte pour comprendre cette
figure expérimentale ?

Dans la formule ci-dessus, la variable x n'apparaît pas. L'éclairement
dépend par contre de la variable y : les franges d'interférences seront
donc horizontales. Les cercles sont dus
au phénomène de diffraction par les deux trous S1 et S2.
Q3. Montrer que
cette figure permet d'estimer les valeurs de la longueur d'onde l0 et de b.
Les franges lumineuses correpondent aux interférences
constructives pour lesquelles cos ( 2 p a y) / ( l0D)) = 1.
2 p
a y / ( l0D)
= 2 k p avec k
entier relatif.
a y / ( l0D)= k
Interfrange,
distance entre deux franges lumineuses consécutives : i = l0D
/ a.
Sur la figure, 1,0 cm correspond à 10 interfranges : i =1,0 10-3
m.
l0=a
i / D=5,0 10-4 x 1,0 10-3 / 1 =5,0 10-7
m.
Largeur de la tache de diffraction : L =2 l0 D / b =
2,0 cm.
b =2 l0 D / L =2 x 5,0 10-7
x 1 /(2,0 10-2) =5,0 10-5 m.
|
...
|
....
|
Expérience de Joule.
En 1843, James Prescott Joule proposa une expérience permettant de
mesurer l'équivalent mécanique de la chaleur.
Une masse m = 3 x101 kg, initialement immobile à une hauteur
H = 2 m, entraîne la rotation d'ailettes lors de son mouvement de
chute. Ce mouvement de translation de la masse m est converti en
mouvement de rotation à l'aide d'un fil inextensible, encastré dans une
poulie et enroulé autour de l'axe de rotation des ailettes. Les
ailettes sont dans une enceinte supposée calorifugée et remplie d'eau (
l'eau est supposée initialement au repos ). On note T la température de
la masse d'eau présente dans l'enceinte et mesurée à l'aide d'un
thermomètre. On néglige tous les frottements, sauf ceux associés à la
viscosité de l'eau présente dans le calorimètre. On donn g = 4 x 101
m s-2.
Le travail des forces de viscosité de l'eau est à l'origine d'une
augmentation de la température T. J.P Joule associe cette élévation de
température à un transfert thermique équivalent Q ( exprimé en calorie
( cal)). La capacité thermique de l'ensemble du calorimètre ( eau,
ailettes et enceinte ) vaut c = 5 kcal K-1. J.P. Joule
effectue à 20 reprises le mouvement de chute de la masse m sur une
hauteur H et note la variation de température DT = 0,6 °C. On note W le
travail mécanique du poids, exprimé en joule (J), mis en jeu lors
des mouvements de chute et A la valeur de l'équivalent mécanique de la
chaleur tel que A = W / Q.
Q1. Déterminer la
valeur de A et interpréter la valeur obtenue.
W = m g H = 3 x 101 x 1 x101 x 2 x 20~1 x 104
J.
Q = c DT = 5 x
0,6 =3 kcal = 3 103 cal.
A =W / Q = 1 x 104 / (3 x 103) ~ 3 J cal-1.
Valeur bien différente de 4,185 J / cal ( écart relatif ~30 %).
L'ensemble des mesures sont peu précises. Toutes les valeurs sont
données avec un seul chiffre significatif.
Autre exemple de conversion d'un travail
en transfert thermique : la bouilloire.
Activité expérimentale en terminale.
Vous avez à disposition une bouilloire, un thermomètre, une balance, un
chronomètre et un wattmètre.
Proposer puis réaliser un protocole permettant d'obtenir le
rendement de la bouilloire.
Mesure de la masse d'eau contenue dans la bouilloire :
Peser la bouilloire vide, puis peser la bouilloire contenant une masse
m d'eau.
Repérer la température initiale de l'eau.
Brancher le wattmètre puis la bouilloire tout en faisant démarrer
le chronomètre.
Relever la température de l'eau au bout d'une minute.
Résultats obtenus :
Température
initiale Ti(°C)
|
Température
finale Tf(°C) |
Masse
d'eau m (kg)
|
Temps
de chauffage Dt
(s)
|
Puissance
moyenne consommée P (W)
|
30,0
±0,5
|
48,5
±0,5
|
1,670
±0,005
|
67,0
±0,5
|
2515
± 5
|
Capacité thermique massique de l'eau c = (4185 ± 1 ) J kg-1 K-1.
Déterminer
le rendement de la bouilloire avec une estimation de son incertitude.
Commenter.
Energie gagnée par l'eau :
Q = m c DT =1,670 x 4185 (48,5-30,0)=1,29 105 J.
Incertitude sur la différence de température : u(DT) =[u(Ti)2+u(Tf)2]½ .
u(DT) =[0,52+0,52]½ =0,7 °C.
Incertitude sur Q : u(Q)= Q [(u(m) / m )2 +(u(c) / c )2 +(u(DT) / DT )2]½.
u(Q)= 1,29 105 [(0,005 / 1,670 )2 +(1 / 4185 )2 +(0,7 / 18,5 )2]½.
u(Q) =1,29 105(9 10-6 +6 10-8 +1,4 10-3)½=4,9 103 J.
Q =(1,29 ±0,05) 105 J.
Energie électrique consommée : E = P Dt=2515 x 67,0 =1,69 105 J.
Incertitude sur E : u(E)= E [(u(P) / P )2 +(u(Dt) / Dt )2]½.
u(E)= E [(u(P) / P )2 +(u(Dt) / Dt )2]½.
u(E)= 2515 [(5 / 2515 )2 +(0,5 / 67 )2]½=2515 [4 10-6 +5,6 10-5]½=19,4 J.
E =(1,69 ±0,0002)105 J.
Rendement : h =Q / E =1,29 105 / (1,69 105)=0,763.
Incertitude sur le rendement : u(h)= h [(u(E) / E )2 +(u(Q) / Q)2]½.
u(h)=0,763 ( 19,4/ (1,69 105 )2 +(4,9 103) / (1,29 105)2]½.
u(h)=0,763 (1,3 10-8 +1,4 103)½ =0,03.
h =0,76 ±0,03.
Il y a des pertes thermiques lors de l'expérience. L'énergie électrique
est utilisée pour chauffer l'eau et les matériaux constituants la
bouilloire.
Expérience de Hertz.
En 1888, Hertz proposa un dispositif permettant de démontrer le
caractère ondulatoire des phénomènes électromagnétiques en utilisant un
oscillateur ( à l'origine de l'émission d'une onde électromagntique
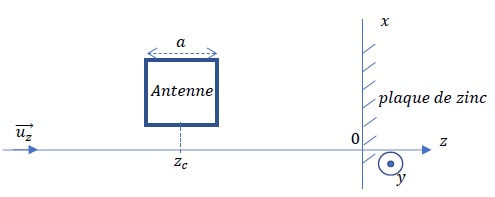
supossée quasi-sinusoïdale et de fréquence h0 = w0 / (2p), une antenne de réception et des plaques de zinc.
La présence d'une plaque de zinc en z=0, supposé être un métal
parfaitement conducteur, permet une réflexion des champs
électromagnétiques dans l'espace z < 0.
Hertz pensait que si le champ électromagnétique était une onde alors,
comme dans le cas de la corde de Melde, la formation d'une onde
stationnaire était possible dans l'espace z <0 par superposition
d'une onde incidente décrite, en représentation complexe par
l'expression 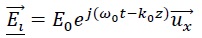 et d'une onde réfléchie décrite par et d'une onde réfléchie décrite par 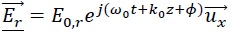 où E0, F, E0,r sont des constantes réelles où E0, F, E0,r sont des constantes réelles
et k0 = w0 / c est le nombre d'onde.
Q1. En admettant que la relation de passage vérifiée par le champ électrique totale s'écrive 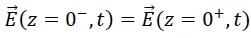 et que le champ électrique soit nul dans le métal, montrer que l'on peut choisir E0 = -E0,r ; F = 0 et que le champ électrique soit nul dans le métal, montrer que l'on peut choisir E0 = -E0,r ; F = 0
Dans l'hypothèse où E0 = -E0,r ; F = 0 :
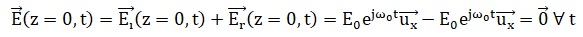
En accord avec un champ électrique nul dans le zinc, conducteur supposé parfait.
Le champ magnétique résultant est donné par l'expression 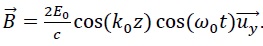
L'antenne de réception est modélisée par un circuit filiforme de géométrie carrée ( côtés de longueur a). On repère par zC le centre de l'antyenne.
Q2. Expérimentalement, on fixe k0a << 1, justifier que l'on puisse approcher le champ magnétique par l'expression 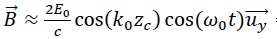 en tout point de la surface de la surface carrée délimitée par le contour de l'antenne. en tout point de la surface de la surface carrée délimitée par le contour de l'antenne.
k0 = 2 p / l ; 2 p a / l << 1.
Si la longueur d'onde l est très supérieure aux dimensions de l'antenne, la variation spatiale du champ électrique est négligeable.
Q3. Déterminer l'expression de la force électromagnétique induite e qui apparaît dans l'antenne en utilisant la loi de Faraday.
e= - dF / dt = -2E0 / c w0 a2 cos(k0 zc) sin (w0t).
Q4. En déduire l'expression de la distance dm entre deux points consécutifs de l'axe Oz où l'amplitude de la fem induite e est maximale.
Deux points distants de dm sont tels que : k0dm = p ; dm = p / k0.
Hertz en observant ces maxima de tension ( qui se traduisaient
par la présence d'étincelles au niveau de l'antenne ) valida la
théorie des champs électromagnétiques. Il mesura dm = 5,0 m.
Q5. Donner la valeur de la fréquence h0 en MHz de l'onde électromagnétique que Hertz devait détecter.
h0 = w0 / (2p) =k0c /(2p) = c /(2dm) =3,0 108 / (2 x 5,0) = 30 106 Hz = 30 MHz.
Etude d'une transmission hertzienne.
On considère une antenne d'émission rayonnant une puissance Pe en direction d'une antenne de réception captant une puissance Ps. La puissance détectée doit être supérieure à une puissance notée Préf afin que la liaison hertzienne puisse être possible. Ces deux antennes sont distantes d'une distance d et on note l << d la longueur de l'onde électromagnétique émise.
Même sans obstacle ( espace libre ), la puissance Ps captée ne représente qu"une fraction de la puissance Pe rayonnée dans l'espce.
Ps / Pe = (l / (4pd))2.
Soit d = 10,0 km la distance entre les deux antennes, on réalise une communication hertzienne à la fréquence de 8,00 GHz.
1. Déterminer, en absence de précipitation, la valeur de l'affaiblissement A donné par A = 10 log ( Pe /Ps) lors d'une transmission entre ces deux antennes.
l = c / n =3,00 108 / (8,00 109)=0,0375 m.
Ps / Pe =(0,0375 / (4 x3,14 x 1,0 104))2 =8,9 10-14.
A = 10 log(1 / (8,9 10-14)) =130,5 dB.
2. A
l'affaiblissement A calculé précédemment vient s'ajouter un
affaiblissement dû aux précipitations. Déterminer la nouvelle
valeur de l'affaibllissement A' en présence de précipitations
dont l'intensité est de 100 mm / h.
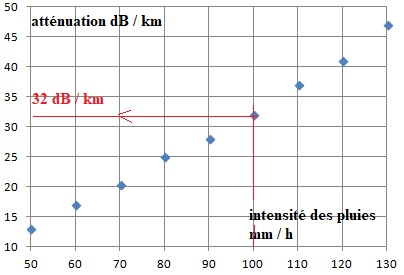
A' = A +32 x10 = 130,5 +320 =450,5 dB.
Principe d'une transmission hertzienne.
Dès les années 1920 ont été établies les premières
radio-télécommunications. Le principe de ces communications consistait
à transmettre un signal utile et analogique u(t) à l'aide d'un autre
signal p(t) appelé porteuse. Avec un modulateur ( réalisant une
modulation d'amplitude), on obtient un signal modulé s(t) qui peut
facilement être rayonné par une antenne après amplification. Une
antenne de réception suivie d'un circuit électroniique de réception
permet ensuite de récupérer le signal u(t).
On pose u(t) = Um cos (wt) ; p(t) = Pm cos (Wt) où Um, Pm, w et W > w sont des constantes.
1. Représenter le spectre du signal s(t) = u(t) x p(t).
s(t) = Um Pm cos (wt) cos (Wt)
s(t) =0,5 Um Pm [ cos ((w+ W)t) + cos (cos ((W- w)t)].
Son spectre est le suivant :
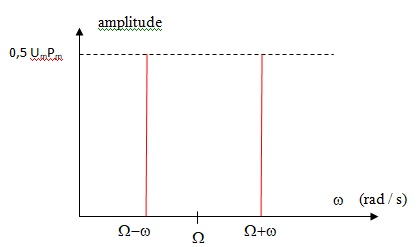
2. Dessiner l'allure du spectre de s(t) dans le cas où u(t) est un signal complexe dont le spectre est le suivant :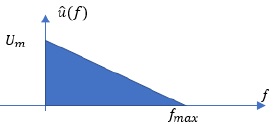
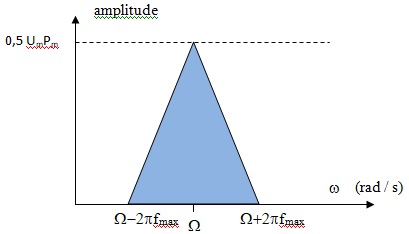
Actuellement, les modulations d'amplitude sont utilisées pour des
communications de courtes distances et utilisent des signaux u(t)
numériques moins sensibles aux bruits. Les moduletions d'amplitudes de
type OOK sont les plus simples car un état haut de u(t) impose s(t) =
p(t) et un état bas de u(t) impose s(t) = 0.
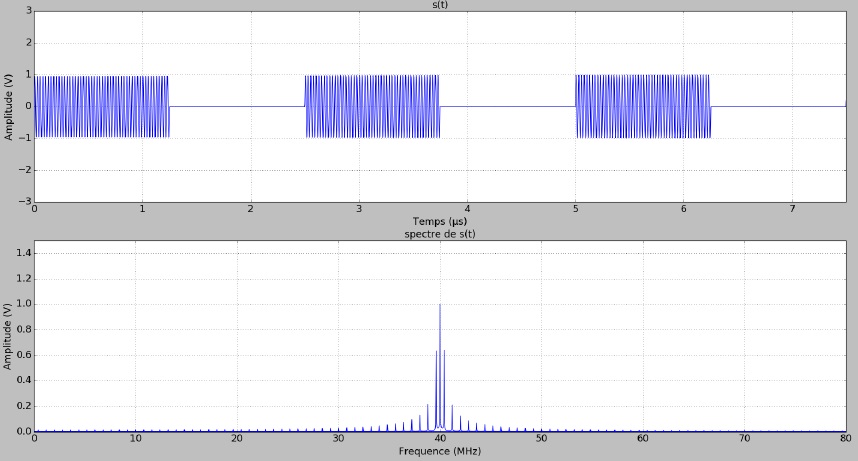
On donne l'oscillogramme et le spectre d'un signal s(t) issue d'une
modulation de type OOK que l'on souhaite transmettre par voie
hertzienne.
Ce signal s(t) est rayonné par une antenne d'émission et sa réception
se fait au moyen d'une antenne et d'un circuit de réception. Ce
circuit de réception contient, entre autres, un filtre passe bande
permettant de conserver s(t) et d'atténuer les signaux de fréquences
différentes que l'antenne de réception a pu capter.
3. On suppose que
le circuit de réception utilisé est constitué uniquement d'un dipôle
résistif de résistance R = 100 ohms, d'une bobine d'inductance L et
d'un condensateur de capacité C. Ce système sélectif présente un
gabarit tel que sa bande passante à -3 dB vaut 10 MHz.
Proposer un schéma de filtre, en précisant les valeurs de L et C permettant de respecter ce gabarit.
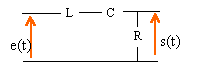 |
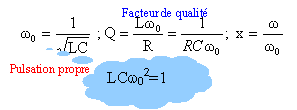 |
Toutes les grandeurs soulignées sont des
nombres complexes.
A ces grandeurs on peut appliquer les lois du courant
continu.
Le pont diviseur de tension conduit à : H(jw) = s /
e
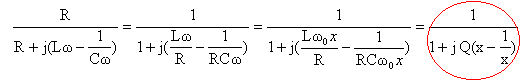
expression du gain
G(w): norme de la
fonction de transfert
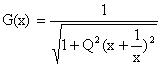
Ce gain est maximum pour x = 1. Gmax = 1.
La pulsation de coupure wc est telle que G = Gmax / 2½.
1+ Q2(x-1/x)2 = 2 ; Q2(x-1/x)2 = 1 ; (x-1/x)2 = 1 / Q2 ;
x-1/x = ±1 / Q soit x2 -x / Q -1 = 0 ou x2 +x / Q -1 = 0.
Discriminant D = 1 / Q2 +4.
On retient les racines positives soit : x1= [1/Q+ (1 / Q2 +4)½ ] / 2 et x2= [-1/Q+ (1 / Q2 +4)½ ] / 2 .
La bande passante est telle que : x1-x2=1 / Q =R / (L w0) soit Dw =R / L.
R = 100 ohms ; Dw =2 p Df =2 *3,14 x1,0 107 =6,28 107 rad / s.
L = 100 / (6,28 107) ~1,6 10-6 H.
C = 1 / (Lw02) =1 / (L 4p2 f02) =1 / (1,6 10-6 * 4*3,142 *(40 106)2) =9,9 10-12 F.
|
|