Expérience
des trous d'Young et applications.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Dans
toute cette partie, l'air possède les propriétés optiques assimilables
à celles du vide.
a. Quelques aspects
historiques.
En 1801, T Young entreprend une expérience d'interférences visant à
démontrer que la lumière visible peut être décrite comme une onde
scalaire : on parle de vibration lumineuse. L'observation expérimentale
de cette figure d'interférences a permis de remettre en cause le modèle
particulaire de la lumière que Newton avait proposé au 17è siècle.
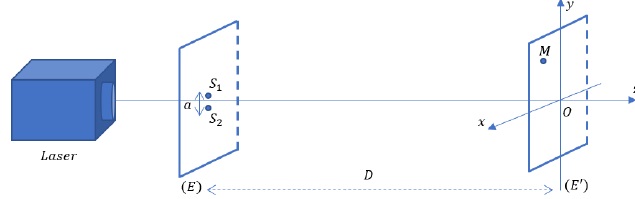
En classe, on peut facilement mettre en évidence l'interférence à deux
ondes lumineuses à l'aide du montage représenté ci-dessous. Il est
constitué :
- d'un laser émettant un faisceau lumineux cylindrique d'axe Oz. Cette
source est supposée monochromatique, de pulsation w et de longueur d'onde l0.
- d'un plan E percé de deux trous circulaires, identiques, de rayon b,
distants de a et centrés sur les points S1 ( 0 , ½a , -D et S2
( 0 , -½a ; -D). Le faisceau éclaire entièrement et de manière uniforme
ces deux trous sources.
- d'un écran de projection E' parallèle à E et situé à une distance D
de (E) telle que D >> a. ( On choisit D = 1 m, a = 0,5 mm). Un
point M quelconque de l'écran (E') est repéré par les variables ( x, y,
0). Le champ d'onservation est tel que |x| << D et |y | <<
D.
Q6. Montrer que
l'éclairement E(M)
en M est donné par : E(M)=
2 E0 [ 1 + cos (
2 p a y) / ( l0D)]
si on considère que les vibrations lumineuses au point M, issues des
deux trous source S1 et S2, sont décrites
respectivement par les
expressions s1(M, t) = S0 cos [wt-2p S1M / l0] et s2(M,
t) = S0 cos [wt-2p S2M / l0]. S0
est une constante. E0 est
l'éclairement qui serait obtenu en masquant l'un des deux trous.
Décrire la figure d'interférences.
Au point M de
l'écran :
vibration
résultante : s(M,t) =s1(M,
t) +s2(M, t)
=S0 ( cos
[wt-2p S1M / l0]+cos [wt-2p S2M / l0] ).
éclairement : E(M)=
< s(M, t)
2>
E(M)= S20
( < cos2
[wt-2p S1M / l0] > + < cos2 [wt-2p S2M / l0] )>+
< cos
[wt-2p S1M / l0].cos [wt-2p S2M / l0] > ).
<
cos2 [wt-2p S1M / l0] > = < cos2 [wt-2p S2M / l0] )>0,5.
< cos [wt-2p S1M / l0].cos [wt-2p S2M / l0] > = <
cos [2wt-2p S1M / l0+2p S2M / l0] >+ <
cos[ 2p S2M / l0-S1M / l0] >.
< cos [2wt-2p S1M / l0+2p S2M / l0] > = 0
E(M)= S20
( 1+ cos[ 2p / l0 (S2M-S1M)] ).
S1M2 =(y-½a)2 +x2 +D2.
S2M2 =(y+½a)2 +x2 +D2.
S2M2 -S1M2 =2ay.
S2M2
-S1M2 =(S2M+S1M)(S2M-S1M)
avec S2M+S1M
~2D.
S2M-S1M~ay
/ D.
E(M)= S20 [
1 + cos ( 2 p a
y) / ( l0D))]
avec S20=2 E0.
Q7.
Comparer l'éclairement calculé à la question précédente avec la figure
ci-dessous obtenue expérimentalement sur l'écran (E'). Quel autre
pphénomène optique doit-on prendre en compte pour comprendre cette
figure expérimentale ?

Dans la formule ci-dessus, la variable x n'apparaît pas. L'éclairement
dépend par contre de la variable y : les franges d'interférences seront
donc horizontales. Les cercles sont dus
au phénomène de diffraction par les deux trous S1 et S2.
Q8. Montrer que
cette figure permet d'estimer les valeurs de la longueur d'onde l0 et de b.
Les franges lumineuses correpondent aux interférences
constructives pour lesquelles cos ( 2 p a y) / ( l0D)) = 1.
2 p
a y / ( l0D)
= 2 k p avec k
entier relatif.
a y / ( l0D)= k
Interfrange,
distance entre deux franges lumineuses consécutives : i = l0D
/ a.
Sur la figure, 1,0 cm correspond à 10 interfranges : i =1,0 10-3
m.
l0=a
i / D=5,0 10-4 x 1,0 10-3 / 1 =5,0 10-7
m.
Largeur de la tache de diffraction : L =2 l0 D / b =
2,0 cm.
b =2 l0 D / L =2 x 5,0 10-7
x 1 /(2,0 10-2) =5,0 10-5 m.
|
...
|
....
|
b) Applications.
La physique quantique associe aux particules une longueur d'onde et
leur confère des propriétés ondulatoires. Afin de mettre en évidence ce
caractère ondulatoire, C. Jönsson réalisa en 1961 des expériences
consistant à envoyer des électrons à travers une ou plusieurs fentes.
On obtient les figures suivantes sur un écran fluorescent.

Soit un électron auquel on associe une longueur d'onde le arrivant en
incidence normale sur une fente fine. On suppose qu'après avoir franchi
cette fente fine, son vecteur quantité de mouvement s'inscrit dans un
cône de demi-angle au sommet q.
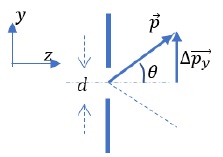
Il existe donc pour cet électron, une indétermination sur la composante
Dpy
de sa quantité de mouvement. De même, l'électron qui passe par la fente
fine, de largeur d, possède une certaine indétermination spatiale Dy dont la valeur peut être
estimée par d.
Q9. On donne la
relation d'indétermination d'Heisenberg qui lie Dy et Dpy telle que Dy . Dpy > h / (4p). Montrer, en utilisant la
relation de de Broglie, que la physique quantique prévoit bien un écart
angulaire minimum qm
de diffraction en fonction de d et le.
Relation de de Broglie : p = h / le
;
Dpy = p sin q = h sin q / le .
La relation d'indétermination d'Heisenberg conduit à d.h sin q / le > h / (4p).
L'angle de diffraction maximale est tel que : sin qm > le / (4pd).
La résolution de la figure d'interférence ( précision maximale avec
laquelle on peut faire des pointés), augmente lorsque le nombre N de
fentes augmente. Cette propriété est mise à profit dans les microscopes
électroniques en transmission.
Les électrons, initialement immobiles, sont accélérés grâce à une
tension U >0 entre une cathode et une anode. Ces électrons sont
supposés non relativistes. Ils sont associés à une longueur d'onde
d'environ un ordre de grandeur plus petit que la distance interatomique
d0. Après accélération et focalisation, ces électrons
atteignent un nombre important d'atomes d'un très mince échantillon.
L'analyse de la figure de diffraction peut permettre ensuite d'étudier
la structure cristalline de l'échantillon.
On donne h ~ 7 10-34 J s ; masse de l'électron me ~9 10-31
kg et la charge élémentaire e ~ 2 10-19 C.
Q10. Donner une
estimation de la valeur de la tension U nécessaire pour analyser un
solide cristallin par l'étude de la figure de diffraction électronique.
Commenter l'hypothèse non relativiste des électrons.
Distance entre deux atomes ( ou deux ions) dans un solide cristallin :
d~1nm soit 10-9 m.
En conséquence le
~10-10 m.
Au cours de son accélération, variation de l'énergie cinétique de
l'électron : e U =Ec finale - Ec début = Ec
finale = p2 /(2me).
e U =(h / le)2
/ (2me).
U = (h / le)2 /
(2 e me) = 72 10-68 / (2 x10-20
x2 10-19 x 9 10-31) ~1 102 V.
Energie cinétique finale de l'électron : e U = 2 10-19 x 102
= 2 10-17 J.
Energie de masse de l'électron : m c2 = 9 10-31 x
32 1016 =8 10-14 J, valeur très
supérieure à l'énergie cinétique finale.
L'électron n'est pas relativiste.
|
|