Capteur de champ électrique, Capes physique chimie 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . .. .. .. ...... ... L’alimentation électrique d’une maison se fait également via le réseau par l’intermédiaire des lignes électriques. Ces dernières rayonnent un champ électromagnétique. Pour vérifier que le champ électrique rayonné n’est pas supérieur aux normes de sécurité (la norme française est 5 × 103 V.m–1), il faut disposer de capteurs de champ électrique. On se propose d’étudier un tel capteur, basé sur un effet capacitif et placé dans la maison. Compte tenu de la valeur de la fréquence des champs électriques à mesurer (f = 50 Hz), on suppose que l’étude peut être conduite dans le cadre de l’électrostatique.  On considère un condensateur plan d’axe z. L’aire des électrodes est notée S. L’électrode 1 (potentiel V1) porte une charge par unité de surface σ (σ > 0). L’électrode 2 (potentiel V2) porte une charge par unité de surface -σ. Elles sont séparées par une distance h. Le condensateur peut être considéré comme infini dans les directions x et y, les effets de bord sont donc négligés.  10. Donner l’expression du champ électrique entre les armatures. La distribution de charge reste invariante suivant les axes x et  y ( pas d'effet de bord). Le champ ne dépend pas de x et de y. Appliquer le théorème de Gauss : la surface de Gauss est un cylindre de section dS. Le flux du champ est nul à travers la surface latérale du cylindre, celle-ci étant perpendiculaire au champ. Valeur du champ uniforme entre les armatures E = s/e0.  La différence de potentiel U = V1 – V2 aux bornes du condensateur s’écrit U = Q/C0 où Q est la charge totale portée par l’électrode 1 et C0 la capacité du condensateur. Déterminer l’expression de C0 en fonction de S, h et ε0. C0 = e0 S / h.  11. Ce dispositif est maintenant plongé dans un champ extérieur, variable dans le temps,  dont la mesure est envisagée. Montrer qu’alors U = Q/C0 – Eext×h. Tension supplémentaire crée par ce champ extérieur : Tension totale entre les deux électrodes : U+U' =Q/C0 – Eext×h. .... 12. 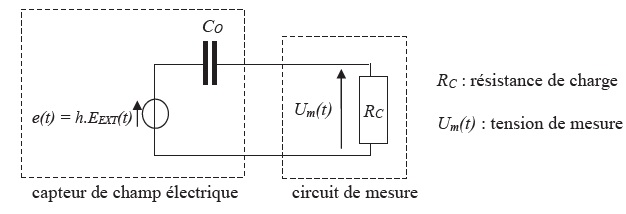Le dispositif peut alors être représenté par le schéma électrique suivant : Déterminer l’équation différentielle vérifiée par Um(t). Loi des mailles : e(t) = uC(t) +Um(t). Um(t)= Rc i(t) ; i(t) = C0dUc(t) / dt ; e(t) = hEext(t). Dériver par rapport au temps :  de(t)/dt = duC(t) /dt +dUm(t)/ dt. de(t)/dt = Um(t) / (RcC0) +dUm(t)/ dt.  13. Le champ électrique Eext(t) varie sinusoïdalement à la pulsation ω = 2πf. On se place en régime sinusoïdal forcé. Montrer que, si RC est très supérieure à une valeur limite Rlim, alors il est possible d’écrire : Um(t) = K × Eext(t). Exprimer Rlim en fonction de C0 et ω, puis la constante K en fonction des données. Sachant que h = 2 mm et que l’amplitude de Um(t) mesurée est 0,8 V, les normes de sécurité sont-elles respectées pour l’habitation située en-dessous de la ligne électrique étudiée ? En notation complexe, l'équation différentielle s'écrit : e(t) = hEext(t)ejwt ; Um(t) = Umejwt ; de(t)/ dt =jw hEext(t)ejwt ; dUm(t)/dt =jw Umejwt . jw hEext(t)ejwt  =Umejwt  / (RcC0) +jw Umejwt . jw hEext(t)  =Um / ( RcC0)  +jw Um . Um =hEext(t) / (1+ 1 /( jwRcC0). Um =hEext / [1+1 / ( wRcC0)2]½. On pose : Rlim =1/(wC0 ). Si Rc >> Rlim  : 1 / ( wRcC0) << 1 et Um =hEext. Eext = Um  / h =0,8 / (2 10-3) =400 V / m <  5 103 V / m ( seuil réglementaire).

menu