Les
complexes du fer, concours agrégation 2019.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Introduction.
1. Comment établir la configuration électronique fondamentale de l'atome de fer (Z = 26).
L'élément fer se trouve dans la quatrième ligne de la classification périodique (n = 4).
C'est le sixième élément de la première série des métaux de transition.
Le gaz noble qui le précède est l'argon.
La configuration électronique fondamentale de l'atome de fer est : [Ar] 4s2 3d6.
[Ar]=1s2 2s2 2p6 3s2 3p6.
2. Définir les électrons de valence et indiquer leur nombre pour le fer.
Les électrons de valence d'un atome sont ceux :
- qui occupent les sous-couches de nombre quantique principal le plus élevé ( n=4 pour le fer, les deux électrons 4s2) ;
- qui occupent les sous couches incomplètes de nombre quantique principal n-1. ( électrons 3d6 pour le fer).
Soit au total : 8 électrons de valence, c'est à dire le numéro de la colonne de cet élément de transition.
3. L'ion fer(II) forme de nombreux complexes octaèdriques. Justifier leur stabilité à l'aide d'une règle simple.
Configuration électronique de Fe2+ :[Ar]3d6, soit 6 électrons de valence.
Règle des 18 électrons : un complexe ayant la même configuration électronique que le gaz noble qui suit l'atome central est très stable.
L'ion fer(II) forme 6 liaisons avec les atomes de ligands, chaque atome
donnant 2 électrons à l'ion fer (II) ; soit 12+6=18 électrons de
valence pour le complexe.
A. Etude de complexes colorés en solution aqueuse par spectroscopie visible.
A.1. Détermination de la constante de formation de l'ion (Fe(SCN)(H2O)5]2+.
4. Ecrire les formules mésomères les plus représentatives de l'ion thiocyanate SCN-.

5. Cet ion est ambidente. Expliquer ce terme.
Cet ion possède deux sites de fixation : l'azote N- et le soufre S-.
6.
Décrire le protocole de fabrication de 250 mL de la solution de nitrate de fer (III) à 0,20 mol / L à partir du solide Fe(NO3)3, 9H2O.
M = 55,8 +3x(14+3x16) +9 x18 =403,8 g / mol.
Quantité de matière : n = 0,250 x0,20 =0,050 mol.
Masse de solide à peser : m = 0,050 x403,8 ~20,2 g.
Introduire cette masse de solide dans une fiole jaugée de 250 mL
surmontée d'un entonnoir à solide ( rincer la coupelle à peser avec de
l'eau distillée).
Ajouter de l'eau distillée dans la fiole jaugée ; agiter jusqu'à
dissolution complète. Compléter jusqu'au trait de jauge avec de l'eau
distillée.
7. Définir par une relation littérale la grandeur absorbance.
On note I0 l'intensité incidente arrivant sur une cuve contenant la substance absorbante et I l'intensité de la lumière transmise.
A = log( I0 / I).
8. Ecrire la loi de Beer-Lambert dans le cas d'une seule substance absorbante. Préciser les conditions de validité de cette loi.
A = e l C.
l : largeur cuve en cm ; C : concentration en substance absorbante en mol / L ; e : coefficient d'absorption molaire de l'espèce absorbante en mol-1 L cm-1.
Les solutions doivent être limpides, très diluées et non fluorescentes.
[Fe(H2O)6]3+aq +SCN-aq = [Fe(SCN)(H2O)5]2+aq +H2O. (1)
9. Pourquoi est-il nécessaire de travailler en milieu acide ?
Il faut éviter la précipitation de Fe(OH)3.
10.
A la longueur d'onde de travail, seuls les deux complexes absorbent.
Donner l'exppression de l'absorbance d'une solution contenant ces deux
complexes.
A = e l [[Fe(SCN)(H2O)5]2+aq] + e'l [[Fe(H2O)6]3+aq].
11.
Expliquer quel est l'intérêt de faire le blanc sur la solution ne
contenant pas d'ions thiocyanate. En déduire l'expression des
absorbances mesurées.
Fe(H2O)6 3+
est introduit en grand excès ; sa concentration peut être considérée
comme constante, peu différente de la concentration initiale. En
faisant le blanc sur une solution ne contenant pas d'ion SCN- : Ablanc = e'l [[Fe(H2O)6]3+aq].
L'absorbance mesurée est alors : A = e l [[Fe(SCN)(H2O)5]2+aq]
12. Pourquoi les résultats de la figure suivante permettent de conclure que la réaction étudiée n'est pas quantitative.
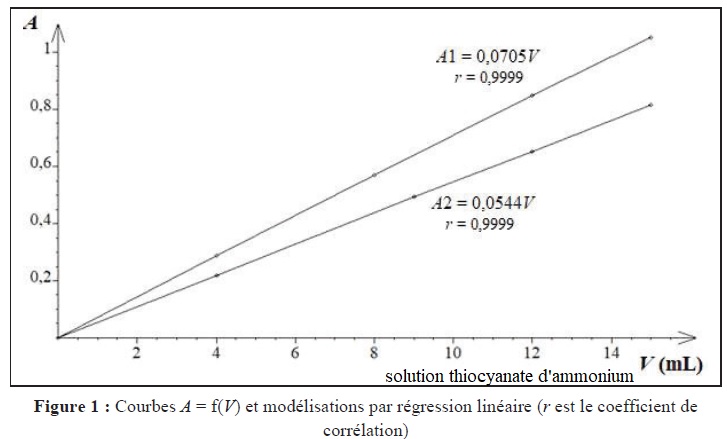
Fe(H2O)6 3+ est introduit en grand excès dans les deux séries de mesures.
Les droites étant distinctes, pour un même volume de SCN- ajouté, la concentration du complexe diffère. La réaction de complexation n'est pas quantitative.
13. Déterminer la valeur de la constante de formation du complexe [Fe(SCN)(H2O)5]2+aq.
|
avancement (mol / L)
|
[Fe(H2O)6]3+aq |
+SCN-aq |
= [Fe(SCN)(H2O)5]2+aq |
+H2O |
initial
|
0
|
C0
|
C
|
0
|
solvant
|
en cours
|
x
|
~C0 |
C-x
|
x
|
à l'équilibre
|
xéq
|
~C0 |
C-xéq |
xéq |
K = xéq / (C0(C-xéq)).
xéq = KC0 /(1+KC0) C.
A = e l xéq = e l KC0 /(1+KC0) C avec C = V Cs / Vfiole ; Cs = 2,0 10-3 mol / L ; Vfiole = 100 mL.
Pente des droites : p = e l KC0 / ((1+KC0)Vfiole) Cs.
Série de mesure n°1 : C0 =0,04 mol / L ; pente p1 =0,0705.
Série de mesure n°2 : C'0 =0,008 mol / L ; pente p2 =0,0544.
Rapport des pentes p1 / p2 = C0 (1+KC'0)/ ((1+KC0) C'0) = 0,0705 / 0,0544 ~1,3.
0,04(1+0,008 K) / (1+0,04K)x0,008 =1,3.
1+0,008K =0,26 +0,0104 K ; K =0,74 / 0,0024 ; K ~309.
|
...
|
....
|
Etude de complexes du fer avec l'ion cyanure.
21. Nommer le complexe [Fe(CN)6]4-.
Hexacyanoferrate(II).
22. Donner les noms et les représentations conventionnelles de O.A d de l'ion Fe2+.
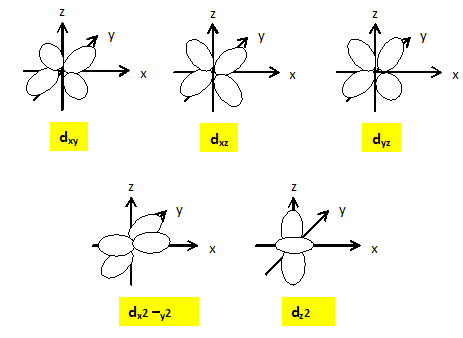
23. Préciser lequel des deux éléments C ou N est le plus électronégatif.
C et N appartiennent à la même période. N est à droite de C, donc N est plus électronégatif que C.
24. Faire la liste des OA à prendre en compte pour construire le diagramme d'OM de l'ion cyanure.
Tenir compte des OA de valence de C (2s, 2px, 2py, 2pz) et de N (2s, 2px, 2py, 2pz). Total : 8 OA.
25. Quels sont les critères généraux pour que des orbitales puissent interagir ?
Les énergies des orbitales doivent être voisines ; le recouvrement des orbitales ne doit pas être nul.
26.
Quelles sont les interactions à considérer pour construire les OM de
l'ion cyanure. On place l'axe nucléaire sur l'axe Oz d'un repère Oxyz.
L'orbitale s est sphérique.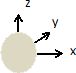
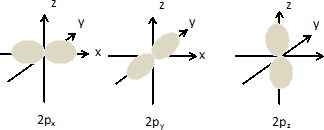
Les orbitales doivent posséder les mêmes propriétés de symétrie.
Interactions à 4 orbitales : 2sC, 2pzC, 2sN, 2pzN conduisent à 4 OM s par recouvrement axial.
Interactions à 2 orbitales : 2pxC, 2pxN conduisent à 2 OM p par recouvrement latéral.
Interactions à 2 orbitales : 2pyC, 2pyN conduisent à 2 OM p par recouvrement latéral.
27. La figure suivante donne le diagramme d'OM de CN-. Indiquer quelles sont les OM s et les OM p. Représenter conventionnellement les OM3 et 6.
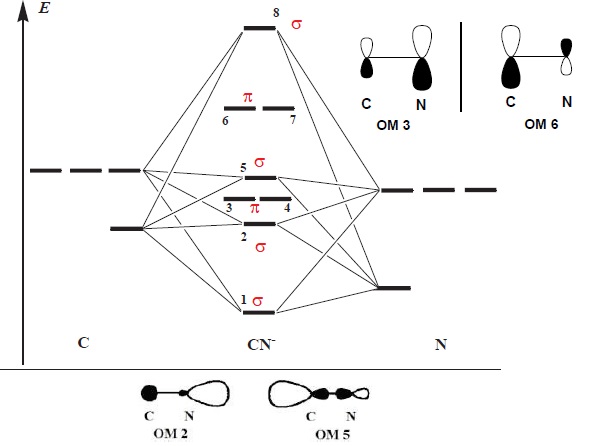
OM 3 ou 4 p liante ; étant plus proche en énergie de l'O A 2pxN, elle est plus développée sur N.
OM 6 ou 7 p antiliante ; étant plus proche en énergie de l'O A 2pxC, elle est plus développée sur C.
28. Quelles sont les orbitales frontières de l'ion cyanure ?
L'ion cyanure possède 4 +5 +1 = 10 électrons de valence occupant les OM de plus basse énergie.
Les orbitales frontières sont la HO la plus haute occupée (OM5) et les BV inocupées de plus basse énergie (OM 6 et 7).
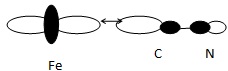
29. Le ligand CN- est s
-donneur. Définir ce terme puis donner un exemple d'interaction
orbitalaire qui explique cet effet. Schématiser cette interaction et
justifier la position spatiale du centre métallique Fe par rapport aux
atomes C et N du ligand.
Un ligand donneur possède une OM occupée par deux électrons ( la HO en
général) ; cette orbitale peut se recouvrir axialement avec une OA du
centre métallique.
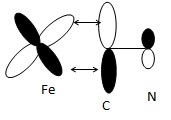
30. Le ligand CN- est p-accepteur.
Définir ce terme puis préciser quelle(s) interaction(s) orbitalaire(s)
explique(nt) cet effet. Schématiser une telle interaction.
Un ligand est p
-accepteur s'il possède une OM vacante ( BV en général) ; cette orbitale peut se recouvrir latéralement avec une OA d du centre métallique.
31. Expliquer quelle est la conséquence de cet effet p-accepteur sur la longueur de la liaison CN dans le complexe par rapport à celle de l'ion libre CN-.
Dans la rétrodonation la liaison CN est affaiblie. La longueur de la
liaison CN croît dans le complexe par rapport à celle de l'ion libre.
|
|