Piézoélectricité. Agrégation 2020
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Jacques et Pierre Curie ont découvert en 1880 l'effet piézoélectrique.
Cet effet est présent dans les matériaux cristallins ne possédant pas
de centre de symétrie. Il se traduit par la capacité de certains
matriaux à se polariser et à faire apparaître des charges électriques
de surface suite à une contrainte mécanique qui les déforme ( effet
direct). La déformation résultant de l'application d'un potentiel
électrique est appelée effet inverse. Un cristal piézoélectrique peut
être utilisé comme capteur et actionneur
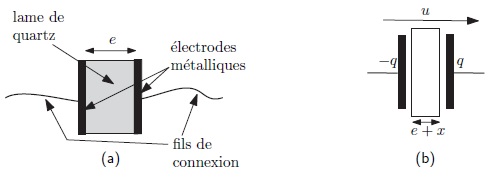
Modèle électrique du quartz.
Un
cristal de quartz est taillé sous forme d'une lame à faces parallèles,
d'épaisseur e. Sur ces deux faces en regaed, on effectue un dépôt
métallique permettant d'obtenir deux électrodes, puis de connecter
l'ensemble à un circuit électrique.
L'application d'une différence de potentiel u entre les électrodes
conduit à l'apparition d'une charge ±q sur celles-ci, et à une
variation d'épaisseur du quartz, d'une quantité algébrique x. La figure
suivante définit les conventions d'orientation.
On admet pour l'instant les équations constitutives (EC).
q / C +ax = u ; mx"+dx'+kx+aq=0.
Les coefficients C, m, d, k et a sont des constantes positives.
1.
Etablir l'équation différentielle reliant la variation d'épaisseur x à
la différence de potentiel appliquée aux bornes du quartz. En déduire
l'équation, notée (E), vérifiée par la vitesse v = x'.
q / C +ax = u donne q = (u-ax) C.
Repport dans mx"+dx'+kx+aq=0 :
mx" +dx' +kx+a(u-ax) C =0.
mx" +dx' +(k-a2C)x= -Cau.
Dériver par rapport au temps : mv" +dv' +(k-a2C)v=-Ca du /dt (E).
2. La
stabilité du système est étudiée pour le régime libre u = 0.
Qu'appelle-t-on stabilité ? A quelle(s) condition(s) portant sur les
coefficients le système est-il stable ?
En
absence d'excitation extérieure ( dans ce cas u =0 ), après avoir subi
un écart à sa position d'équilibre, un système est stable y revient.
Si u = 0, l'équation (E) s'écrit : mv" +dv' +(k-a2C)v= 0.
Equation caractéristique : mX2 +dX+(k-a2C)=0.
Discriminant D =d2-4m(k-a2C).
Si D >0, l'équation possède deux racines reélles notées X1 et X2.
Si ces deux racines sont négatives, le système est stable.
X1X2 =(k-a2C) / m >0 soit (k-a2C) >0.
X1+ X2 = -d /m < 0.
3. Dans toute la suite, on supposera que k > Ca2. Réécrire l'équation (E) en utilisant les grandeurs :
w0 =[(k-Ca2) / m]½ et Q = mw0 / d.
v" +d / m v' +(k-a2C) / m v= -Ca / m du /dt.
v" +w0 / Q v' +w02 v= -Ca / m du /dt.
4. On suppose que u(t) est un échelon de tension : u(t) = 0 pour t <0 et u(t)=E=constante pour t >0
Le cristal de quartz est initialement au repos. Pour Q > 0,5, montrer que la solution v(t) de cette équation peut se mettre sous la forme v(t) = A e-t / t sin(w'0t).
Si t < 0, u(t) =0 et v(t) = 0.
Si t >0 : u(t) = Cste ; du /dt =0.
v" +w0 / Q v' +w02 v= 0.
Discriminant D = w0 2 / Q2-4w02 =w02 (1 / Q2-4)=w02 (1 -4Q2)/ Q2.
D < 0 si Q > 0,5.
Racines de l'équation : X = -w0 /(2Q) [1±j(4Q2-1)½].
Donner les expressions de t et w'0 en fonction de Q et w0. Que dire de w0 lorsque Q >> 1 ; à quelle situation physique cette limite correspond-elle ?
t =2 Q / w0 ; w'0 = w0 / (2Q) (4Q2-1)½.
La solution générale de (E) vérifiant v(t=0)=0 est : v(t) = A e-t/t sin ( w'0t) avec A une constante.
Lorsque Q >>1, w'0 ~w0, l'oscillateur oscille à la pulsation propre de l'oscilateur non amorti.
5. On définit le temps de réponse tq du quartz comme le temps au bout duquel l'enveloppe du signal est inférieure à 5 % de sa valeur initiale. Exprimer tq en fonction de Q et de la pseudo-période d'oscillation. En déduire une interprétation de Q.
L'enveloppe du sigal est v0(t) =A e-t / t .
De plus v0(t) < 0,05 v0(0) ; v0(t) < 0,05 A.
e-t / t < 0,05 ; t > t ln (1/0,05) ; t > t ln (20) ~3 t.
tq = t ln (20) = 2 Q ln(20) / w0~6 Q / w0.
Pseudo-période d'oscillation T ' = 2p / w'0.
tq =T ' w'0 Q ln(20) / (w0 p)~ T ' w'0 3 Q / (w0 p) ~ T ' w'0 Q / w0 .
De plus si Q >>1, w'0 ~ w0 et tq ~ T' Q.
Interprétation de Q : nombre d'oscillations du système précédant une diminution d'amplitude de 5 % de la valeur initiale.
On travaille à présent en notation complexe, le quartz étant alimenté par un générateur de pulsation w.
6. Le courant i parcourant la quartz est défini en convention récepteur. Définir, puis calculer à partir de (EC), l'impédance complexe Z du dipôle. Celle-ci sera exprimée en fonction de w, k, a, C, d et m.
7. On cherche à montrer que ce comportement est équivalent à celui du dipôle électrique suivant.
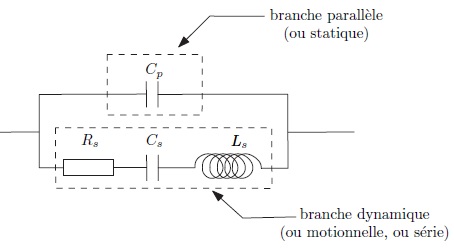
Circuit électrique équivalent à la lame de quartz.
Calculer l'impédance équivalente Ze de ce modèle. Par identification, vérifier qu'elle se comporte comme Z. Donner les valeurs de Cs, Rs, Ls et Cp en fonction de C, a, m, d et k.
i = j w q.
Les équations notées (EC) s'écrivent :
q / C+ ax =u. (1)
mx"+dx'+kx+aq=0. (2)
x' = j w x ; x" = -w2 x ;
(-m w2 + d j w + k ) x+aq=0.
On pose A = -m w2 + d j w + k.
A x + aq=0.
(1) donne : x =(u - q / C)/ a ; par suite A (u - q / C)/ a + aq=0.
u - q / C+ a2q / A=0 ; u = q [ 1/ C- a2 / A] =i / (jw)[ 1/ C- a2 / A].
Z = u / i = 1 / (jw)[ 1/ C- a2 / A].
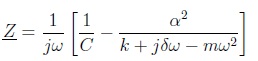

On identifie : C = Cp ; Cs =a2C2 /(k-Ca2) ; Rs = d / (a2C2) ; Ls = m / (a2C2)
8. Dans les quartz réels, on peut avoir Q ~105, de sorte que R est très faible. On étudie dans cette question le cas Rs =0.
Exprimer l'impédance Z. Comparer ws à w0.
Pulsation de résonance série : ws2 = 1 /(Ls Cs) ;
Ls Cs=m / (k-Ca2); par suite ws =w0, pulsation propre du quartz.
Pulsation de résonance parallèle : wp2 =(Cp+Cs) / (LsCsCp).
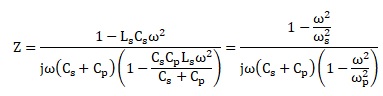
Pourquoi parle t-on de résonance en ws et d'antirésonance en wp ? Que vaut le courant dans la branche série à w = ws ?
Z est nulle si w = ws : le courant parcourant le quartz est donc très grand. Il s'agit d'une résonance en courant.
Z est infinie si w = wp : le quartz n'est parcouru par aucun courant, il se comporte comme un interrupteur ouvert, il s'agit d'une antirésonance.
Les valeurs typiques sont de l'ordre Cp ~10-12 F et Cs ~10-14 F. Calculer le paramètre (wp2-ws2) / ws2 et donner sa valeur numérique. Qu'en conclure sur la position de ces deux pulsations ?
(wp2-ws2) / ws2 = wp2 / ws2 -1 =[ (Cp+Cs) / Cp]2-1 =1,012-1= 0,02.
Les deux pulsations sont très proches.
Proposer une expression approchée de (wp2-ws2) / ws2 en fonction de l'écart relatif entre ws et wp.
(wp2-ws2) / ws2 =(wp - ws ) (wp + ws )/ ws2 ~2 (wp - ws ) / ws.
9. On suppose que Rs
diffère de zéro. On veut justifier que la résonance et l'antirésonance
sont bien visibles séparément. Le facteur de qualité Q représentant le
rapport entre la pulsation de résonance et la bande passante,
donner la largeur de la résonance et la comparer à l'écart entre ws et wp. Si Q = 100, séparerait-on la résonance de l'antirésonance ?
Bande passante : Dw =w0 /Q = ws / Q.
Dw / w0 = 1 / Q = 10-5.
(wp - ws ) / ws =0,01.
Dw / w0 << (wp - ws ) / ws .
La résonance et l'antirésonance sont bien séparées. Ce serait faux si Q = 0,01.
|
....
|
Piézoélectricité.
Le quartz est un cristal de formule stoechiométrique SiO2.
On y taille une lame mince. Selon l'orientation de cette lame par
rapport au réseau cristallin, un effet piézoélectrique peut apparaître
: en 1880 J et P Curie ont découvert qu'une traction ou une compression
du cristal conduisent, en plus d'une variation de dimensions, à
l'apparition d'une polarisation du milieu.L'effet inverse est également
visible : le dépôt de charges sur les faces d'une lame piézoélectrique
conduit à l'allongement de celle-ci.
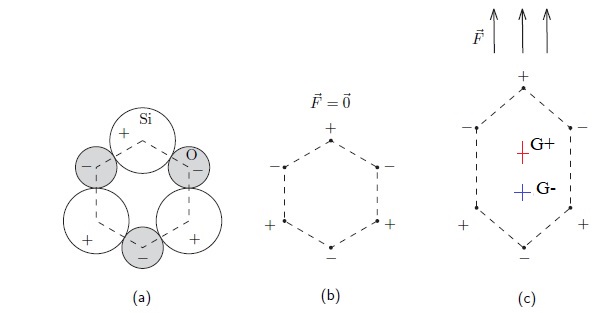
a. Coupe d'une maille d'un cristal de quartz ; b : position des charges
lorsqu'aucune force n'est exercée ; c : le cristal est étiré
verticalement.
17. Justifier
que l'étirement conduit à l'apparition d'un moment dipolaire local,
donc d'une polarisation. Donner son sens et sa direction.
Figure b
: absence d'étirement, le barycentre des charges positives et le
barycentre des charges négatives sont confondus, situés au centre de la
maille hexagonale.
Figure c :
étirement vers le haut. Le barycentre des charges positives est au
dessus du barycentre des charges négatives. Donc, il existe un moment
dipolaire dirigé vers le haut. La polarisation a la même direction et le même sens que la force.
18. Pour une lame
mince rectangulaire, d'épaisseur e et de surface S, étirée
perpendiculairement à ses grandes faces, donner les densités
surfaciques de charge apparaissant sur ces faces. En supposant la
polarisation uniforme, montrer qu'elles sont opposées l'une à l'autre.
On les notera ±sp avec sp >0.
Face supérieure, densité surfacique sP positive.
Face inférieure, densité surfacique -sP négative.
19. On réalise un
dépôt métallique sur les grandes faces de la lame de quartz. On
s'intéresse à l'interface métal-quartz, lorsque celle-ci porte une
densité surfacique de charge s. A l'aide des propriétés de discontinuité du vecteur déplacement, montrer que 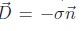 à la surface du quartz piézoélectrique. à la surface du quartz piézoélectrique.
On note : 1 le quartz et 2 l'armature métallique.
A l'interface de ces deux milieux, le vecteur déplacement subit la discontinuité normale :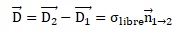
Dans le métal, à l'équilibre : 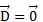
A la surface du quartz : slibre = s.
En conséquence, à la surface du quartz piézoélectrique : 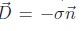
20. La lame de quartz métallisée est étirée par une force 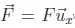 de sorte que son épaisseur devient e +x avec |x| << e. La
polarisation du quartz doit inclure un terme piézoélectrique ; cet effet
étant linéaire, on en rend compte en introduisant la constante a telle que, dans le quartz :
de sorte que son épaisseur devient e +x avec |x| << e. La
polarisation du quartz doit inclure un terme piézoélectrique ; cet effet
étant linéaire, on en rend compte en introduisant la constante a telle que, dans le quartz :
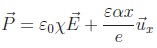
où e =e0er est la permitivité diélectrique totale du quartz et c sa susceptibilié.
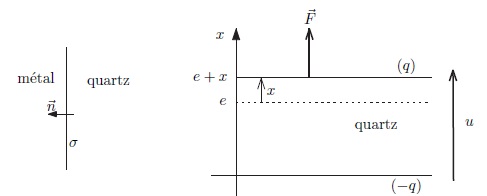
Donner le champ électrique dans la lame en fonction de x et de la
charge q portée par l'armature du haut. En déduire que la différence de
potentiel aux bornes des armatures métalliques est : q / C + a x = u. (CEM1).
Dans le quartz, entre les aramtures métalliques, le champ électrique et
la polarisation sont uniformes. ( condensateur plan et milieu linéaire,
homogène et isotrope ). Il en est de même du vecteur dicontinuité
normale.
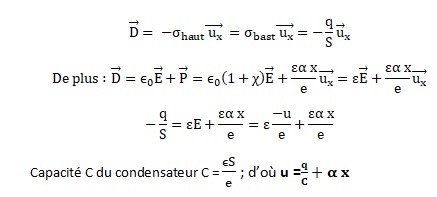
21. L'effet
piezoélectrique inverse se traduit de même par une force due à la
charge q qui s'ajoute au pur effet de l'allongement. La force de
traction à exercer s'écrit alors F = kx +a q ( CEM2). les deux équations ( CEM1) et (CEM2) traduisent ainsi le couplage électromécanique existant dans une lame piézoélectrique.
A charge nulle ( q = 0), quelle propriété mécanique l'équation (CEM2) traduit-elle ? A quelle grandeur mécanique k est-il relié ?
Pour q =0, (CEM2) s'écrit : F = k x, traduisant l'élasticité du milieu.
k est lié au modèle de Young e du quartz.
F / S = e x / e ; F = e x S / e = kx.
22. A force nulle, quelle est à présent la capacité apparente de l'ensemble {lame + électrodes } ?
On admet que les paramètres obtenus dans les questions précédentes
restent valables en régime dynamique. On admettra alors que les
variations d'épaisseur x de la lame de quartz peuvent être modélisées à
l'aide de l'équation diférentielle :
mx"+dx'+kx+aq=0
où m est une masse effective et d un coefficient positif.
Si F = 0, x = -aq / k.
Par suite u = q / C -a2q / k = q / C'.
La capacité apparente de l'ensemble C' = C / ( 1-Ca2 / k ) est supérieure à celle d'une lame non piézoélectrique.
23. A partir des équations constitutives(EC), effectuer un bilan
énergétique dans la lame. On pourra l'écrire en termes de puissance
sous la forme :
Pélectrique = Pfrottements + d /dt (Ecinétique + Eélastique +Econdensateur + Eem)
Identifier chacun des termes.
Multiplions par i = q' la première équation : q / C +ax = u ;
q'q / C +ax q' = u i.
Multiplions par la vitesse x' de déplacement du centre d'inertie de la lame la seconde équation : mx"+dx'+kx+aq=0.
mx"x'+dx'2+kxx'+aq x'=0.
dérivée par rapport au temps de (aq x) : a(q x'+ q' x).
La somme des deux équations donne :
u i =d x'2+d / dt [ 0,5 m x'2 +0,5 kx2 +0,5 q2 / C +aq x].
Pélectrique = Pfrottements + d /dt (Ecinétique + Eélastique +Econdensateur + Eem).
Pélectrique : puissance fournie par le générateur.
Pfrottements : puissance dissipée par les frottements.
0,5 m x'2 : énergie cinétique.
0,5 kx2 : énergie élastique.
0,5 q2 / C : énergie stockée dans le condensateur.
aq x : couplage entre la charge et l'allongement ( énergie électromécanique).
|
|