Principe
de l'échographie, échographie Doppler.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Principe
de l'échographie.
Les ondes ultrasonores sont utilisées pour réaliser des
échographies du corps humain.
1.
Aux fréquences utilisées en échographie médicale ( 2 à 20 MHz) les
tissus mous du corps possèdent des propriétés acoustiques voisines de
celles de l'eau. La taille des plus petits détails observables sur ces
images est de l'ordre de la longueur d'onde. Estimer cette dernière
pour la gamme de fréquences utilisées.
Célérité des ondes dans l'eau : c = 1,4 103 m /s.
l = c
/ n ; 1,4 103
/ (2 106) =7 10-4 m ; 1,4 103 / (2 107)
=7 10-5 m.
L'impédance
acoustique Z a pour expression Z = r0 c avec r0 masse
vvolumique du fluide et c : célérité de l'onde dans le fluide.
A l'interface entre deux milieux d'impédances acoustiques Z1
et Z2,
les expressions des coefficients de transmission T et de réflexion R
d'une onde se propageant du milieu 1 vers le milieu 2 et arrivant en
incidence normale sur la surface, s'écrivent :
R = (Z2-Z1)2 / (Z2+Z1)2
; T =4Z1Z2 / (Z2+Z1)2
.
2.
Evaluer les ordres de grandeurs des coefficients de réflexion à
l'interface tissus mous-air et tissus mous-os. Pourquoi utilise t-on un
gel échographique entre la sonde et le corps humain ? Pourquoi est-il
difficile de réaliser des échographies du cerveau ?
Zair = 0,4 103 kg m-2 s-1
; Zos =7,8 106 ; Z tissus mous ~1 106 .
A l'interface tissus mous-os : R =
(8 106- 106)2 / ( 8 106+ 106)2
~0,6.
A l'interface tissus mous-air : R =
(106-0,4 103)2 / ( 106+0,4 103)2
~1.
Les ondes ne pénètrent pas dans le corps humain. Le gel permet de faire
une adaptation d'impédance. Les ondes pénètrent dans le corps et les
échos reçus permettent de construire une image.
Le coefficient de réflexion à l'interface tissus mous - os est grand.
L'énergie du signal qui arrive au cerverau est faible.
Il faut ensuite que le signal revienne vers la sonde avec à nouveau de
grands coefficients de réflexion. L'énergie du signal de retour vers la
sonde est faible et il est impossible de réaliser des échographies du
cerveau.
3. En échographie,
on utilise une sonde composée de capteurs piézoélectriques. Quel est le
principe physique utilisé par ces capteurs ? Quand et par qui fut-il
découvert ?
L'effet piézoélectrique fut découvert par les frères Curie à la fin du
XIXème siècle.
Un matériau piézoélectrique soumis à une contrainte se polarise
électriquement. En réciproque, soumis à un champ électrique, il se
déforme.
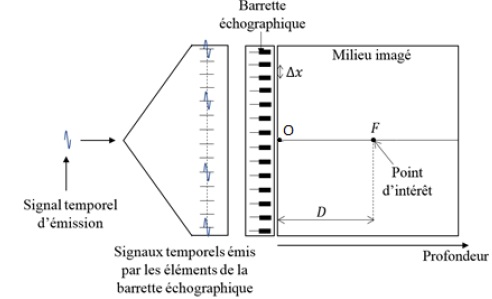
Afin de réaliser une image échographique, on utilise un réseau linéaire
de N = 128 capteurs fonctionnant en émission et en réception. Ils
constituent la barette échographique. Chaque élément de cette
barette est numéroté. Les capteurs au dessus du centre de la sonde
échographique sont numérotés de i = 1 à i = N / 2, ceux au-dessous du
centre de la sonde sont numérotés de i = -1 à i = -N /2. Ils sont
espacés d'une distance Dx
=1 mm sur la barette échographique et émettent des impulsions
temporelles très courtes de l'ordre d'une microseconde.
4. Quel est le
nombre typique de périodes contenues dans une impulsion ?
La fréquence des ondes est de l'ordre du mégahertz. Pour une fréquence
de 10 MHz, la période est égale à 1 / 107 = 0,1 µs.
Une impulsion dure 1 µs et contient une dizaine de périodes.
Les capteurs émettent tous en même temps la même impulsion. Les signaux
rétrodiffusés par le milieu suite à cette émission sont enregistrés par
N éléments de la barette qui passent en mode réception. On disposent
donc de N signaux rétrodiffusés qu'il faut exploiter. On désire
extraire la contribution du point F au centre de l'image, situé à une
distance D de la sonde échographique. Pour cela, on somme les N signaux
rétrodiffusés et reçus par les capteurs en les décalant dans le
temps afin que les N contributions au point F soient en phase.
L'intensité associée à ces N signaux est codée en niveau de gris sur
l'image échographique. C'est l'étape de focalisation en réception.
5. Déterminer le
décalage temporel ti
à appliquer au signal reçu par le capteur i de la sonde par rapport à
un signal fictif reçu en O, en fonction de D, c, i et Dx. Faire l'application
numérique pour D = 6 cm et c = 1,5 103 m /s..
Distance di entre les capteurs situés en i > 0 et -i :
di =[ (| i |-½)2Dx2+D2]½.
Décalage temporel ti
= di / c -D/c.
Décalage maximal i = 64 : di =[ (64-½)2 10-6+0,062]½~0,0874
m.
ti = di
/ c -D/c = (0,0874-0,06 ) / (1,5 103)=1,8 10-5 s.
En pratique, l'étape d'émission est plus compliquée. l'image
échogtaphique est découpée en 128 lignzs orthogonales à la barette. On
choisit une profondeur de focalisation et on expose séquentiellement le
milieu à des faisceaux ultrasonores focalisés à cette profondeur sur
chaque ligne. Par conséquent, il y a 128 émissions pour réaliser une
image. C'est l'étape de focalisation en émission. 7.
Le temps d'acquisition de la signature acoustique d'une ligne de
l'image est fixé par le temps d'aller-retour des signaux ultrasonores
jusqu'à la profondeur maximale imagée. Calculer ce temps pour une
profondeur maximale imagée L= 10 cm.
2L / c = 0,20 / (1,5 103) =1,33 10-4 s.
8.
Calculer le temps minimal de réalisation de l'image échographique de
128 lignes. En déduire le nombre maximal d'images par seconde réalisées
par cet échographe. Peut-on dire que ce dernier fait de l'imagerie en
temps réel ?
1,33 10-4 x 128 =0,017 s.
Nombre maximum d'images réalisées par seconde : 1 /0,017 ~58.
Cet
échographe fait de l'imagerie en temps réel.
|
....
|
Echographie Doppler.
Le
échographes peuvent superposer à l'image standard une visualisation des
flux sanguins grâce à une mesure de vitesse en utilisant l'effet
Doppler.
L'émetteur émet une onde monochromatique de fréquence fem se
propageant à la vitesse c dans le milieu. Le récepteur reçoit une onde
de fréquence frec alors qu'il se rapproche de l'émetteur.

1.
Etablir l'expression de l'écart de fréquence Df = frec-fem
entre l'émission et la réception en fonction de v, c et fem.
On s'intéresse, dans un premier temps, au cas où une onde ultrasonore de fréquence fem est émise par le transducteur immobile en direction d'un globule rouge se rapprochant de lui à la vitesse de module v constant.
On appelle x0 la coordonnée de P ( globule ) à l'instant t=0.
x(t) = -vt + x0.
A l'instant t=0, S émet des ultrasons qui voyage vers P à la vitesse c.
Instant t1 auquel P reçoit les ultrasons : t1 = x(0) / c = x0 / c.
A l'instant t = Tem :
Le globule récepteur se trouve à la distance x = x0 -v Tem.
Instant t2 auquel le globule reçoit le signal :
t2 = x( Tem) / c =Tem +( -v Tem + x0) / c = Tem - v Tem / c + t1 = Tem ( 1 - v / c) + t1.
Période Trec = t2-t1 du phénomène "vu" dans le référentiel du globule.
Trec = Tem ( 1 - v / c) ; 1 ) ; frec= fem / (1 - v / c).
frec(1 - v / c)= fem ; frec-fem = v / c fem.
Dans le cas médical, la barette
échographique est fixe et joue le rôle de l'émetteur et du récepteur.
Les globules présents dans le sang réfléchissent l'onde ultrasonore.
2. Montrer que dans ce cas l'écart de fréquence entre les signaux émis par la barette Dftot s'écrit en utilisant le fait que v << c :
D ftot =fem 2v / c.
L'onde subit un premier effet Doppler après réflexion sur le globule
mobile et revient vers le capteur fixe en subissant un second effet
Doppler.
Double effet Doppler :
Ttot = Tem ( 1 - v / c)2.
ftot= fem / (1 - v / c)2.
ftot (1 - v / c)2= fem .
ftot(1-2v / c+(v / c)2)= fem .
(v / c)2 étant négligeable devant v / c : ftot(1-2v / c)= fem.
D ftot =ftot -fem =fem 2v / c.
Considérons une onde ultrasonore de fréquence fem = 2 MHz se propageant dans un milieu à la vitesse c = 1500 m /s et un réflecteur se déplaçant à la vitesse v = 5 cm /s.
3. On utilise un
oscilloscope numérique. En voie 1, on enregistre le signal émis et en
voie 2, le signal reçu. Est-il possible de réaliser la mesure de D ftot pour en déduire la vitesse du réflecteur avec cet oscilloscope ? Justifier.
On donne : la fréquence d'échantillonage minimale est 4 MHz ;
l'oscilloscopz utilise 2500 points d'enregistrement sur chaque voie.
D ftot =2 106 x 2 x 5 10-2 / 150 =1,3 103Hz.
La fréquence minimale mesurable est donc : 4 106 / 2500 = 1,6 103 Hz, valeur supérieure à 1,3 103 Hz.
La mesure de D ftot n'est pas réalisable et on ne peut pas en déduire la vitesse du réflecteur.
4. Une méthode de mesure consiste à utiliser une détection synchrone dont le fonctionnement est schématisé ci-dessous :

Quelles sont les fréquence et amplitudes des raies du spectre du signal
en sortie du multiplieur si les signaux émis et reçus ont la même
amplitude A ? On note km le coefficient multiplicateur du multiplicateur.
Le signal émis est de la forme A cos (2p fem t).
Le signal reçu est de la forme : A cos (2p (fem +Df)t +j).
Signal sortant s(t) =kmA2 cos (2p fem t) cos (2p (fem +Df)t +j).
s(t) = 0,5 kmA2 [ cos (2p Df t+j) +cos (2p (2fem+ Df )t+j) ].
Le signal comporte 2 raies :
une raie de fréquence Df et d'amplitude kmA2 /2 et une raie de fréquence 2fem+ Df et d'amplitude kmA2 /2.
5. Proposer
le schéma d'un filtre du premier ordre en sortie du multiplieur pour
extraire l'information nécessaire à la mesure de v ? Donner les valeurs
précises des caractéristiques des composants.
Il faut extraire la composante basse fréquence de fréquence Df. On utilisera un filtre passe bas.
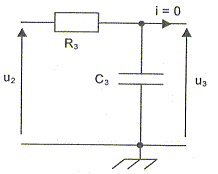
u2 = s(t) ; u3 = s filtrée (t).
La fréquence de coupure est fc = 1 /(2pRC).
Df << fc << 2fem.
1,3 103 << fc << 4 106.
Pour R = 100 ohms et C =1 µF : fc = 1 /(2 x3,14 x100 x10-6) = 1,6 103 Hz.
|
|