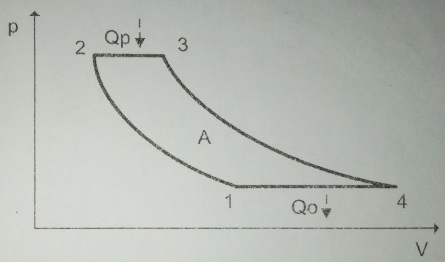
Physique générale (université Abdou Moumouni, Niamey), 06 / 2020. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Cycle de Joule-Brayton. Il est formé de deux isobares reliés par deux adiabatiques. Le cycle est supposé réversible. et décrit dans le sens moteur par un gaz parfait. On pose a = P2 / P1. Calculer le rendement en fonction de a et g. A.N : a = 8 : g = 1,4. Premier principe sur le cycle : Wcycle +Qp +Qo =0. ( pas de chaleur échangée sur les adiabatiques). -Wcycle =Qp +Qo . Sur les isobares : Qp = Cp(T3-T2) ; Qo = Cp(T1-T4). Sur les adiabatiques réversibles: P11-g T1g =  P21-g T2g = Cste ; a = P2 / P1 = (T1 / T2) g /(1-g). T1 / T2 = a(1-g)/g ; T1 =T2 a(1-g)/g. P11-g  T4g =   P21-g T3g = Cste ;  a = P2 / P1 = (T4 / T3) g /(1-g). T4 / T3 = a(1-g)/g ; T4 =T3 a(1-g)/g. T1 / T2 =T4 / T3 . Rendement = -Wcycle / Qp  =1+Q0 / Qp. |Q0| / Qp = (T1-T4) / (T3-T2) = (T2-T3) a(1-g)/g /  (T3-T2) = - a(1-g)/g . Rendement =1-a(1-g)/g  = 1- 1 / a(g-1)/g  =1-1/80,4 / 1,4 ~0,45. ... .... La voiture et le piéton. 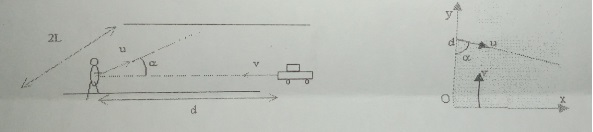Une voiture de largeur L = 1,4 m se déplace à vitesse constante v = 72 km / h en suivant le bord de la route de largeur 2L. Un piéton est à la distance d = 50 m devant la voiture. Il veut traverser à vitesse constante notée u ( a = 45°). 1. Déterminer les coordonnées des vecteurs positions du piéton et de la voiture dans le repère indiqué. 2. Quelle est la valeur minimale de u afin que le piéton ne soit pas touché ? ( le piéton atteint l'abscisse x = L avant que la voiture ne le touche). Piéton : Vecteur vitesse ( u sin a ; -u cos a). Vecteur position : u sin a t ; -u cos a t +d. u sin 45 t ; -u cos 45 t +50 Voiture : Vecteur vitesse : (0 ; v). Vecteur position du bord extérieur : 1,4 ; vt. 1,4 ; 72 / 3,6 t soit 1,4 , 20 t. Le piéton n'est pas touché si : u sin 45 t > 1,4 et -u cos 45 t +50 > 20 t. Cas limite : t  =1,4 /(sin 45 u). -u cos 45 x1,4 /(u sin 45)+50 = 20x1,4 / (u sin 45). -1,4+50 = 39,6 / u. u =39,6 / 48,6 ~0,81 m /s. 3. Pour quelle valeur de a, la vitesse du  piéton est-elle minimale ? Quelle est sa valeur ? Le piéton traverse perpendiculairement à la route ( a = 90°) et doit parcourir au minimum 1,4 m tandis que la voiture doit parcourir 50 m à la vitesse de 20 m /s. t = 50 /20 = 2,5 s ; vitesse minimale du piéton : 1,4  /2,5 =0,56 m /s.

menu