Mathématiques
BTS groupe D 09/20.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1.
A. Evolution de la population de poissons au fil des mois dans certains aquariums.
1.
Dans un aquarium, il y a initialement 10 poissons. La population
augmente de 30 % chaque mois. Quel est le nombre de poissons au bout de
5 mois ? 12 ; 50 ; 160 ; 37 vrai.
10 x1,35 =37.
2. Dans un
aquarium, au temps t =0, il y a 10 poissons. On modélise le nombre de
poissons présents dans l'aquarium par une fonction g. Cette fonction
est solution de l'équation différentielle y' +0,3 y =0 vérifiant la
condition initiale g(0 ) =10.
g est définie par : g(t) = 10e0,3t ; g(t) = 10e-0,3t vrai ; g(t) = 10+ e0,3t ; g(t) = 10+ e-0,3t.
Solution générale de l'équation différentielle : g(t) = A e-0,3 t, avec A une constante.
g(0) = 10 = A.
Partie B. Etude statistique.
On cherche à évaluer l'effet d'un pesticide que l'on peut trouver dans
les rivières, sur la diminution de la fertilité d'une population de
poissons. On dispose de 8 aquariums contenant chacun 10 poissons de la
même espèce et de l'eau avec différentes quantités de ce pesticide. Au
bout d'un mois on relève le nombre total d'oeufs pondus par les
poissons des différents aquariums.
Numéro de l'aquarium
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
Concentration en pesticide ( mg / L) xi.
|
0
|
1
|
4
|
5
|
6
|
7
|
8
|
10
|
Nombre d'oeufs pondus Ni
|
249
|
248
|
246
|
230
|
130
|
50
|
40
|
35
|
| yi= -ln(250 / Ni-1). |
5,52
|
4,82
|
4,12
|
2,44
|
0,08
|
-1,39
|
-1,66
|
-1,86
|
Un ajustement affine n'est pas approprié. On effectue un changement de variable y = -ln(250 / N-1).
1. Compléter le tableau.
2 et 3. Déterminer le coefficient de corrélation linéaire de la série statistique (xi ; yi). Interpréter. Déterminer une équation de la droite d'ajustement.
y = -0,857 x +5,905.
y dminue de 0,859 chaque fois que x augmente de 1 mg / L.
4.
On note N(x) la fonction modélisant le nombre d'oeufs pondus dans un
aquarium en un mois, en fonction de la concentration x en pesticide (
en mg / L).
a. Vérifier que n(x) est solution de l'équation 250 / N(x)-1 = e0,857 x-5,905.
y = -0,857 x +5,905= -ln(250 / N-1).
ln(250 / N-1)=0,857 x -5,905.
250 / N-1= e0,857 x-5,905.
b. En déduire que N(x) = 250 / (1+e0,857 x-5,905).
250 / N(x)=1+ e0,857 x-5,905.
N(x) /250 = 1 /(1+ e0,857 x-5,905)
N(x) = 250 / (1+e0,857 x-5,905).
Partie C. Etude de fonction.
On considère la fonction définie sur [0 ; +oo[ par f(x) =250 / (1+0,003 e0,9x).
1. Calculer la limite de f(x) en plus l'infini.
e0,9x tend vers plus l'infini ; 1+0,003 e0,9x tend vers plus l'infini ; f(x) tend vers zéro.
2.a. Vérifier que f '(x) = -0,675 e0,9x / (1+0,003 e0,9x)2.
On pose u = 250 ; v =1+0,003 e0,9x ; u' = 0 ; v' =0,003 x0,9e0,9x =0,0027e0,9x ;
(u'v-v'u) / v2 =(-250*0,0027e0,9x) / (1+0,003 e0,9x)2.
f '(x) = -0,675 e0,9x / (1+0,003 e0,9x)2.
b. Etudier le signe de f '(x) et donner le sens de variation de f(x).
e0,9x et (1+0,003 e0,9x)2 sont positifs.
f '(x) < 0 et f(x) est strictement décroissante.
3. Tracer la courbe représentative de f(x).
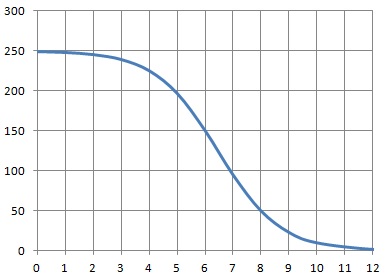
Par
la suite on admet que la fonction f modélise le nombre d'oeufs pondus
par mois dans un aquarium, en fonction de la concentration x en
pesticide ( mg / L) sur l'intervalle [0 ; 50 ].
4. La concentration
efficace médiane CE50 est la concentration qui correspond à une
diminution de 50 % du nombre d'oeufs pondus par mois par rapport à une
eau sans pesticide. Déterminer cette concentration CE50 à 0,1 près.
250 / (1+0,003 e0,9x) = 125 ; 1+0,003 e0,9x = 2 ; 0,003 e0,9x = 1 ;
e0,9x = 1 /0,003 ; 0,9x = ln(1/0,003) ~5,809 ; x ~ 5,809 / 0,9 ~6,5 mg / L.
5. On donne une primitive de f(x) : F(x) = -2500 / 9 ln(e-0,9x+0,003).
Estimer à l'unité près, le nombre d'oeufs pondus par mois, pour des concentrations en pesticide comprises entre 4 et 6 mg / L.
(F(6) / F(4) ) / (6-4).
-2500 / 18[ ln(e-0,9x6+0,003)- ln(e-0,9x4+0,003)] ~ -138,89 (-4,89 +3,495 ) ~ 194.
|
...
|
....
|
Exercice 2.
A. Taux d'hémoglobine chez les femmes en France.
L'anémie se définit par un taux d'hémoglobine dans le sang inférieur ou égal à 12 g / dL.
Une femme est en polyglobulie si son taux d'hémoglobine est supérieur ou égal à 16 g/ dL.
Soit T la variable aléatoire associée le taux d'hémoglobine. T suit la loi normale d'espérance µ =14 et d'écart type s = 1,15.
1. Déterminer la probabilité qu'une femme soit en anémie.
P(T < 12) =0,041.
2. En déduire sans la calculatrice, la probabilité qu'une femme soit en polyglobulie.
P(T >16)=P(T < 12) =0,041, par raison de symétrie.
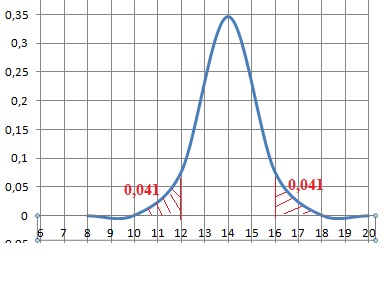
B. prévisions d'erreurs d'analyses.
Un laboratoire procède à 300 d'analyse de taux d'hémoglobine
chaque mois. La probabilité qu'une analyse soit erronée est 0,005. On
note X la variable aléatoire qui, à tout échantillon de 300 analyses,
associe le nombre d'analyses erronées de cet échantillon.
1. Quelle loi suit la variable X ? Justifier et donner les paramètres de cette loi.
Les prélevements sont indépendants et leur nombre est fixé à n = 300.
Chaque
tirage peut déboucher seulement sur 2 résultats : la probabilité
qu'une analyse soit erronée est constante p = 0,005. La
probabilité qu'une analyse soit bonne est q = 1-p = 0,995.
La loi binomiale B(n=300, p = 0,005) est valide.
2.a. Déterminer la probabilité qu'aucune des 300 analyses ne soit erronée.
P(X =0) =0,22.
b. Calculer P(2 < X < 4) et interpréter.
P(X =2) + P(X=3) +P(X=4) =0,251 75 +0,125 67 +0,04689 ~0,42.
La probabilité qu'il y ait 2, 3 ou 4 analyses erronées est égale à 0,42.
C. Délai des résultats des analyses.
Le laboratoire affirme que le délai moyen est de 60 minutes.
On souhaite tester cette hypothèse à l'aide d'un test bilatéral au
seuil de 95 %. On note m le délai moyen pour fournir le résultat.
Hypothèses : H0 : m = 60 et H1 : m diffère de 60.
On admet que 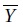 suit la loi normale d'espérance m et d'écart type 1,5. suit la loi normale d'espérance m et d'écart type 1,5.
b. Calculer la valeur du réel h, tel que sous l'hypothèse H0, on ait : P(60 -h < 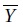 < 60 +h) =0,95.. < 60 +h) =0,95..
h = 1,96 s =1,96 x 0,1,5 ~2,94.
2. Enoncer la règle de décision du test.
Intervalle de confiance :[60-2,94 ; 60 +2,94) soit [57,06 ; 62,94].
Si la moyenne appartient à cet intervalle, H0 est valide, sinon H1 est valide.
3.
Sur un échantillon de 100 analyses,
on a relevé un déai moyen de 62,5 minutes. Que peut-on en conclure ,
62,5 appartient à l'intervalle [57,06 ; 62,94] ; l'hypothèse H0 est valide.
|
|