Mathématiques
BTS groupe C 09/20.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1.
A
la sortie d'un four, un solide dont la température est de 70°C est
placé, pour le refroidir, dans une pièce dont la température ambiante
reste constante égale à Tamb = 20°C. Le solide peut être
emballé pour expédition dès que sa température passe au dessous de
40°C. On désigne par T(t) la température de l'objet en °C du solide à
l'instant t ( exprimé en minute).
T ' (t) représente la vitesse de refroidissement de l'objet à l'instant
t. La loi de Newton établit que cette vitesse est proportionnelle à la
différence de température du solide et de la température ambiante, soit
:
T '(t) = k (T(t) - Tamb) où k est une constante.
Partie A.
1. La constante k dépend des matériaux. Pour le solide k = -0,007. Montrer que T est solution de l'équation différentielle :
(E) : y '+0,07 y = 1,4.
T '(t) = k (T(t) - Tamb) = -0,07 (T(t) +0,07 x20 = -0,07 T(t) +1,4
T '(t) +0,07 T(t) = 1,4.
2. Résoudre dans [0 ; + oo[, l'équation différentielle (E0) : y' +0,07 y = 0.
y = A e-0,07 t avec A une constante.
3 . QCM. Une solution particulière de (E) est la fonction définie par :
f(t) = 20 vrai ; f(t) = 1,4 ; f(t)= 20 t.
4. En déduire la solution générale de (E).
y = A e-0,07 t +20.
5.a. Donner T(0).
T(0) = 70.
b. Déterminer une expression de la température du solide à l'instant t.
T(t) = A e-0,07 t +20 ; T(0) = 70 =A+20 ; A = 50.
T(t) = 50e-0,07 t +20.
Partie B.
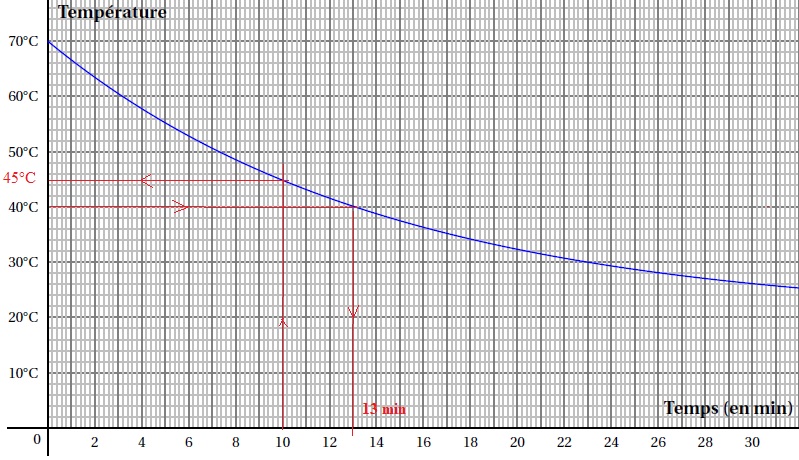
On admet que t(t) = 50e-0,07 t +20. On donne C la courbe représentative de la fonction T.
1. A l'aide du graphique :
a. Déterminer la température du solide au bout de 10 minutes.
b. déterminer au bout de combien de temps le solide peut être emballé pour expédition.
2.a. Etablir les variations de T sur [0 ; +oo[.
Dérivée T ' = 50 x(-0,07) e-0,07t = -3,5 e-0,07t .
e-0,07t >0, donc T ' < 0 et T est strictement décroissante.
b. Expliquer pourquoi la température du solide ne peut atteindre 18 °C.
Le solide est dans une pièce dont la température est maintenue constante à 20 °C.
c. Déterminer au dixième près la température moyenne du solide lors des 10 premières minutes.
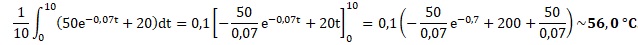
|
...
|
....
|
Exercice 2.
A. Le tableau suivant donne l'évolution des ventes de vélos à assistance électrique en France entre 2007 et 2017.
année
|
2007
|
2009
|
2011
|
2013
|
2015
|
2017
|
rang de l'année xi
|
0
|
2
|
4
|
6
|
8
|
10
|
nombre vélos vendus ( milliers) ni
|
10
|
23
|
37
|
57
|
102
|
278
|
yi=ln(ni)
|
2,30
|
3,13
|
3,61
|
4,04
|
4,62
|
5,63
|
Données : observatoire du cycle.
1. a. Compléter le nuage de points.
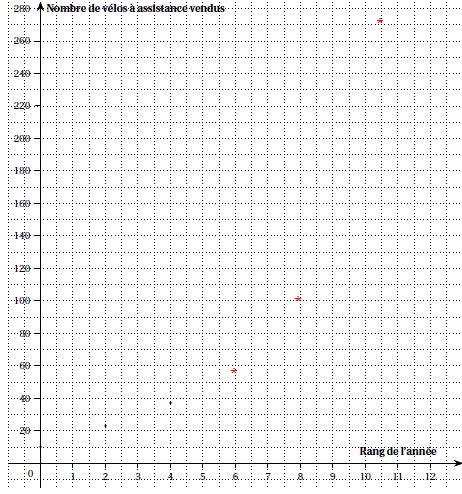
b. Expliquer pourquoi un ajustement affine ne semble pas envisageable.
Les points ne sont pas alignés.
2. On pose yi = ln(ni). Compléter la dernière ligne du tableau.
3. On s'intéresse à l'ajustement affine de yi en fonction de xi.
y =0,3074 x +2,3528.
Si l'évolution se poursuit de la même manière, quel devrait être en milliers le nombre de vélos vendus en 2020 ?
x =13 ; y = 0,3074 x13 +2,3528 =6,349.
n = e6,349 ~572 milliers.
B .
On étudie l'autonomie en km de ces vélos. Soit X la variable aléatoire
qui, à chaque vélo pris au hasard dans la production, associe son
autonomie en km. X suit la loi normale de moyenne µ =81 et d'écart type
s = 4.
1. Déterminer P(X > 84).
P(X > 84) = 1 - P(X < 84) = 1-0,773 =0,227.
2. QCM.
Une valeur approchée à l'unité du réel d tel que P(X < d)=0,1 est : 88 ; 81 ; 76 vrai . Interpréter le résultat.
La probabilité que l'autonomie soit inférieure à 76 km est égale à 0,10.
C. 4 % des
batteries présentent un défaut et sont non conformes. Soit Y la
variable aléatoire qui, à tout lot de 100 batteries pris au hasard dans
la production, associe le nombre de batteries non conformes.
1. Quelle loi suit la variable Y ? Justifier et donner les paramètres de cette loi.
Les prélevements sont indépendants et leur nombre est fixé à n = 100.
Chaque
tirage peut déboucher seulement sur 2 résultats : la probabilité
qu'une batterie soit non conforme est constante p = 0,04. La
probabilité qu'une batterie soit conforme est q = 1-p = 0,96.
La loi binomiale B(n=100, p = 0,04) est valide.
2.a. Déterminer P(Y < 5).
Y =0, ou 1, ou 2, ou 3, ou 4.
P(Y < 4) =0,629.
b. Interpréter ce résultat.
La probabilité qu'il y ait moins de 5 batteries non conforme est égale à 0,629.
3. Déterminer la probabilité que dans ce lot toutes les batteries soient conformes.
P(Y = 0)=0,017.
4. Calculer E(Y) et interpréter.
E(Y) = n p = 100 x0,04 = 4.
En moyenne, il y a 4 batteries non conformes dans un lot de 100 batteries.
|
|