Mathématiques
BTS Opticien-lunetier 05/21.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1.(10 points).
En
vue de la commercialisation d'un nouveau modèle de lunettes solaires,
une grande chaîne de magasins d'optique réalise une anquète auprès de
10 000 clientse coût de revient pour la production d'une paire de lunettes de ce modèle s'élève à 55 €.
A. Ajustement d'un nuage de points.
1. Compléter la
troisième ligne du tableau.
Prix à l'unité € (x)
|
60
|
80
|
120
|
160
|
Nombre d'acheteurs potentiels ( N(x)
|
3000
|
2000
|
900
|
400
|
z = ln(N(x))
|
8,00
|
7,60
|
6,80
|
5,99
|
2. Déterminer une équation de la
droite d'ajustement du nuage de points.
z = -0,02 x +9,21.
3. Montrer que N(x) =10 000 e-0,02x.
ln(N(x)) =-0,02 x +9,21.
N(x) = e-0,02x * e9,21 ~10 000 e-0,02x.
4. Estimer le nombre d'acheteurs potentiels si le prix de vente est de 100 € la paire.
N(x) = 10 000 e-2 ~1353.
B. Modèle discret.
1.a. Montrer que deux diminutions successives de 33 % correspondent à une diminution globale de 55 %.
Prix payé : 100(1-0,33) = 67 ; 67 (1-0,33) ~45.
Diminution 100-45 = 55 ; ( 55 %).
b. A chaque augmentation du prix de 20 €, le nombre d'acheteurs potentiels diminue d'environ 33 %. Justifier.
(3000-2000) / 3000 ~0,33 ( 33 %) ;
(2000-900) / 2000 ~0,55 soit 2 diminutions successives de 33 %.
(900-400) / 900 ~0,55 soit 2 diminutions successives de 33 %.
c. Déterminer le réel q positif tel que q20 = 0,67.
ln(q20) = ln(0,67) ; 20 ln(q) = ln(0,67) ; ln (q) = ln(0,67) / 20 ~ -0,02.
q = e-0,02 ~0,98.
2. Hypothèse : chaque augmentation d'un euro du prix entraîne une diminution de 2 % du nombre d'acheteurs potentiels.
On considère la suite (un) définie par :
u0 = 10 000 ; un+1 = un-0,02 un.
a.
Justifier que (un) est une suite géométrique.
un+1 = 0,98un : suite géométrique de raison 0,98.
b. Exprimer un en fonction de n.
un = u0 x0,98n = 10 000 x0,98n.
c. Calculer u100.
u100 = 10 000 x0,98100 ~1326.
C. Modèle continu.
On considère l'équation différentielle (E) : y' +0,02 y = 0.
1. Déterminer les solutions de (E).
f(x) = A e-0,02 x avec A une constante.
2. Déterminer la solution qui vérifie f(0) = 10 000.
1000 = A e0 = A ;
f(x) = 10 000 e-0,02 x .
D. Etude de la fonction f(x) = 10 000 e-0,02x sur [0 ; +oo[.
On pose B(x) =(x-55) f(x).
1. On donne la dérivée de B(x) : B '(x) = -200(x-105) e-0,02x.
a. Donner le signe de B'(x) sur [0 ; 300].
e-0,02x > 0 ; -200 < 0.
Si x appartient à [0; 105], B'(x) >0.
Si x appartient à [105; 300], B'(x) < 0.
b. Donner le tableau de variations de B.
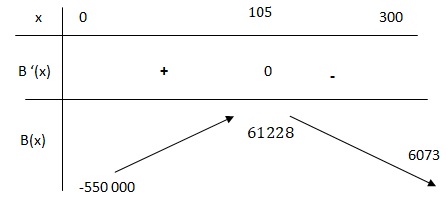
2.a Justifier que B(x) représente le bénéfice en euros.
Nombre de ventes : f(x).
Coût de production d'une paire : 55.
Prix de vente d'une paire : x.
Bénéfice sur une paire (x-55).
Bénéfice : (x-55) f(x).
b. Quel est le prix de vente pour un bénéfice maximum ?
105 €.
|
...
|
....
|
Exercice 2. (10
points).
Une entreprise fabrique des branches de lunettes de trois types appelés type1, type 2 et type 3.
A. Loi normale.
Une
branche de lunette de type 1 est considérée comme acceptable si sa
longueur exprimée en mm est comprise entre 149 et 151 mm. Une branche
est prélevée au hasard dans la production. On note X la variable
aléatoire qui, à chaque branche associe sa longueur.
X suit la loi normale de moyenne 150 et d'écart type 0,5.
1.QCM. La valeur approchée de la probabilité qu'une branche de lunette soit acceptable est : 0,95 vrai ; 0,98 ; 0,99.
P(X < 149) =0,02275 ; P(X < 151) =0,9772 ; P(149 < X < 151) =0,9545 ~0,95.
2. A l'aide de la feuille de calcul suivante, déterminer le plus grand nombre réel a tel que P(X > a) >0,96.
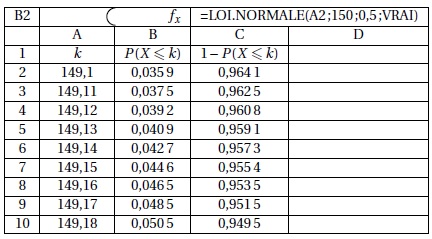
a = 149,12.
B. Loi binomiale et loi de Poisson.
On
considère un nombre important de branches de type 2. Dans ce stock, 2 %
des branches de lunettes ne sont pas acceptables. On prélève au
hasard 100 branches de ce stock. On note Y la variable aléatoire, qui à
tout prélévement de 100 branches, associe le nombre d'entre elles qui
ne sont pas acceptables.
1.a Justifier que Y suit une loi binomiale
dont on précisera les paramètres.
On choisit 100 branches de manière identique, indépendante. Deux issues sont
possibles " la branche est acceptable " ou" la branche n'est pas acceptable".
On répète 100 fois une épreuve de Bernoulli.
Y suit une loi binomiale de paramètre n =100 ; p = 0,02.
b. Calculer la probabilité P(Y < 2).
P (Y < 2)=0,677 ~0,68.
2. On admet que l'on peut approcher la loi de probabilité de Y par une loi de Poisson.
a. Déterminer le paramètre de cette loi.
l = np = 100 x0,02 = 2.
b. On note Y1 une varaible aléatoire qui suit cette loi de Poisson. Calculer la probabilité P(Y1 < 2).
P (Y1 < 2)=0,677 ~0,68.
C. Test d'hypothèse.
La norme prévoit que la longueur des branches de type 3 est de 150 mm.
On note Z la variable aléatoire qui, à chaque branche prélevée dans la
production, associe sa longueur en mm. Z suit une loi normale de
moyenne inconnue µ et d'écart type 0,5.
On désigne par Zmoy la variable aléatoire qui, à chaque échantillon de 100 branches prélevées, associe la moyenne de leurs longueurs.
Hypothèse nulle H0 : µ = 150.
Hypothèse alternative H1 : µ diffère de 150.
Seuil de signification du test : 0,05.
1. Sous l'hypothèse nulle H0 on admet que Zmoy suit une loi normale de moyenne 150 et d'écart type 0,5 / 100½ = 0,05.
Sous cette hypothèse, déterminer un réel positif h tel que P(150-h < Zmoy < 150 +h).
P(150-2s < Zmoy < 150 +2s).
h = 2s = 2 x 0,05 = 0,1.
2. Enoncer la règle de décision permettant d'utiliser le test.
Si Zmoy est compris entre 149,9 et 150,1 l'hypothèse H0 est retenue au risque d'erreur de 5 %. Sinon on retient H1.
3.
Un contrôleur prélève un échantillon de 100 branches. Il constate que
la moyenne des longueurs est 150,2 mm. Quelle sera sa décision ?
150,2 n'appartient pas à [149,9 ; 150,1]. L'hypothèse H0 est rejetée ; l'hypothèse H1 est retenue.
|
|