Mathématiques BTS Opticien-lunetier 09/20.

Mathématiques BTS Opticien-lunetier 09/20.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.. ..

.
.

.. ..
......

...
Exercice 1.(10 points).
La fabrication de verre minéral résulte d'une fusion à 1500 °C de trois éléments ( quartz, potasse et oxyde). Le verre liquide est ensuite acheminé à une presse automatique qui produit des ébauches de verres, lesquels sont refroidis lentement jusqu'à température ambiante.
A. Statistiques à 2 variables.
1. Expliquer pourquoi le changement de variable en posant z =ln(1500 /(1500-T)) est pertinent.

temps ( en minutes) (t)
0
1
2
3
4
5
10
15
20

Température du verre°C (T)
24
354
614
816
943
1066
1395
1459
1491

z = ln(1500 /(1500-T))
0,016
0,269
0,527
0,795
0,991
1,240
2,659
3,600
5,116

Série (t ; T) : les points ne sont pas alignés, une corrélation linéaire est impossible.
Série (t ; z) : les points sont alignés, une corrélation linéaire est possible.

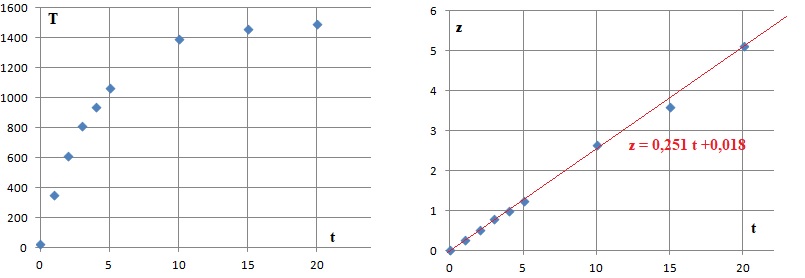
2. Déterminer une équation de la droite d'ajustement du nuage de points.
z = 0,251 t +0,018.
3. Donner une expression de T en fonction de t de la forme T = A e^-0,251t +1500 où A est arrondi à l'unité.
ln(1500 /(1500-T)) =0,251 t+0,018.
1500 /(1500-T)) =e^{0,251 t} x e^0,018.
1500 /(1500-T)) =e^{0,251 t} x1,018.
1500 /(1500-T)) =1,018 e^{0,251 t} .
1500 / (1,018 e^0,251t) = 1500-T.
1476 e^-0,251t = 1500-T.
T = 1500-1476 e^-0,251t.

B. Résolution d'une équation différentielle.
On modélise la température du verre minéral ( °C) par une fonction du temps t (min), solution de l'équation différentielle (E) :
y' +0,25 y = 375.
1. Déterminer les solutions de l'équation différentielle (E₀) : y' +0,25y = 0.
y = A e^-0,25t avec A une constante.
2.a. Vériifier que la fonction g(t) = 1500 est solution de (E).
g'(t) = 0 ; repport dans (E) : 0,25 x1500 = 375.
b. En déduire les solutions de (E).
y = A e^-0,25t +1500.
3. A l'instant t=0, les éléments constitutifs du verre sont à 24°C. Déterminer la fonction h donnant la température du verre.
24 = A e⁰ +1500.
A = 24-1500 =-1476.
h(t) = -1476 e^-0,25t +1500.

C. Etude d'une fonction.
On considère la fonction f(t) = -1476 e^-0,25t +1500.
On donne sa dérivée f '(t) = 369 e^-0,25t.
1. Déterminer le sens de variation de la fonction f sur [0 ; +oo[.
e^-0,25t > 0 ; f '(t) = 369 e^-0,25t >0 ; la fonction f(t) est strictement croissante.
2. QCM.
a. La limite en plus l'infini de f(t) est : 0 : 24 ; 1500, vrai ; 1476.
e^-0,25t tend vers zéro si t tend vers plus l'infini.
b. La courbe C admet une saymptote dont l'équation est :
t = 1500 ; y = 0 ; y = 1476 ; y = 1500 vrai.
c. Une équation de la tangente à la courbe au point d'abscisse 0 est :
y = 369t +24 vrai ; y = 369t-24 ; y = 369 +24t ; y = 369t -369 / 8 t².
Coefficient directeur de la tangente : f '(0) = 369.
Le point de coordonnée (0 ; f (0) = 24 ) appartient à la tangente.
y = 369 t +b ; 24 = 369 x 0 +b ; b = 24.

D. Etude d'une suite.
La température du verre doit subir un abaissement régulier afin que le verre se solidifie sans se cristalliser. On modélise l'évolution de la température du verre en fonction du temps à l'aide de la suite (u_n) définie par :
u₀ = 1500 ; u_n+1 = 0,9 u_n +2,4.
On pose v_n = u_n-24.
1. Montrer que la suite (v_n) est géométrique dont on précisera la raison et le premier terme.
v_n+1 = u_n+1-24.
v_n+1 =0,9 u_n+2,4-24.
v_n+1 =0,9 u_n - 21,6 = 0,9(u_n-24) =0,9 v_n.
(v_n) suite géométrique de raison 0,9 et de premier terme 1476.
2.a. En déduire une expression de v_n en fonction de n.
v_n = 1476 x 0,9ⁿ.
b. Montrer que u_n = 1476 x 0,9ⁿ+24.
v_n = u_n-24 ; u_n = v_n+24 = 1476 x 0,9ⁿ+24.
3. Déterminer la limite de la suite (u_n) et interpréter.
-1 < 0,9 <1 ; 0,9ⁿtend vers zéro quand n tend vers plus l'infini et u_n tend vers 24.
Au bout d'un temps suffisamment long, le verre prend la température ambiante.
4. On considère l'algorithme suivant :
n =0
u = 1500
Tant Que u > 25
u =u x0,9 +2,4
n = n+1
Fin Tant Que
A la sortie de cet algorithme, n = 70. Que représente ce nombre dans ce contexte ?
La température du verre descend en dessous de 25 °C au bout de 70 minutes.

...

....

Exercice 2. (10 points).
Une entreprise fabrique des tiges en titane de longueur 80 mm.
A. Loi normale.
Une tige est considérée comme acceptable si sa longueur exprimée en mm est comprise entre 79,63 et 80,37 mm. Une tige est prélevée au hasard dans la production. On note X la variable aléatoire qui, à chaque tigee associe sa longueur.
X suit la loi normale de moyenne 80 et d'écart type 0,16.
1. Calculer la probabilité qu'une tige ne soit pas conforme.
P(X < 79,63) =0,01037 ; P(X < 80,37) =0,9896 ; P(79,63 < X < 80,37) =0,979.
Probabilité qu'une tige ne soit pas conforme : 1-0,979 ~0,021.
2. Calculer la probabilité P(X < 80,28).
P(X < 80,28) ~0,960.

B. Loi binomiale et loi de Poisson.
Dans un lot de ce type de tiges, on considère que 2 % des tiges n'ont pas une longueur conforme. On prélève au hasard n tiges de ce lot pour vérifier sa longueur. Le lot est assez important pour que l'on puisse assimiler ce prélevement à un tirage avec remise de n tiges.
On considère la variable aléatoire Y qui, à tout prélèvement de n tiges, associe le nombre de tiges de longueur non conforme.
1.Justifier que Y suit une loi binomiale dont on précisera les paramètres.
On choisit n tiges de manière identique, indépendante. Deux issues sont possibles " la tige est acceptable " ou" la tige n'est pas acceptable".
On répète n fois une épreuve de Bernoulli.
Y suit une loi binomiale de paramètre n ; p = 0,02.
2. On prend n = 50. Calculer la probabilité qu'il y ait exactement 2 tiges de longueur non conforme dans ce prélèvement.
P(Y = 2) =0,186.
3.a On considère n = 200. La varible Y peut être approchée par une loi de Poisson. Déterminer le paramètre de cette loi.
l = np = 200 x0,02 = 4.
b. On désigne par Z la variable aléatoire suivant cette loi de Poisson. Calculer la probabilité d'avoir au plus 3 tiges non conformes.
P(Z < 3) =0,433.

C. Test d'hypothèse.
Un client reçoit un lot important de tiges de ce type. On souhaite construire un test d'hypothèse, pour décider, au seuil de 5 %, si on peut considérer que la moyenne des longueurs des tiges reçues est égale à 80 mm. On note L la variable aléatoire qui, à une tige prélevée au hasard dans ce lot, associe sa longueur en mm. L suit la loi normale de moyenne inconnue µ et d'écart type 0,16.
On désigne par L_moy la variable aléatoire qui, à chaque échantillon de 100 tiges prélevées, associe la moyenne de leurs longueurs.
Hypothèse nulle H₀ : µ = 80.
Hypothèse alternative H₁ : µ diffère de 80.
Seuil de signification du test : 0,05.
1. Sous l'hypothèse nulle H₀ on admet que L_moy suit une loi normale de moyenne 80 et d'écart type 0,16 / 100^½ = 0,016.
Sous cette hypothèse, déterminer un réel positif h tel que P(80-h < L_moy < 80 +h).
P(80-2s < Z_moy < 80 +2s).
h = 2s = 2 x 0,016 = 0,032.
2. Enoncer la règle de décision permettant d'utiliser le test.
Si L_moy est compris entre 80-0,032=79,968 et 80,032 l'hypothèse H₀ est retenue au risque d'erreur de 5 %. Sinon on retient H₁.
3. Un client prélève un échantillon de 100 tiges. Il constate que la moyenne des longueurs est 80,02 mm. Quelle sera sa décision ?
80,02 appartient à [79,968 ; 80,032]. L'hypothèse H₀ est retenue.

D. Evénements indépendants.
On contrôle aussi le défaut de courbure des tiges. On constate sur la production d'une journée que 2 % des tiges ont un défaut de longueur et que 5 % des tiges ont un défaut de courbure.
On prélève au hasard une tige dans la production. On note les événements suivants :
B " la tige a un défaut de longueur".
C : " la tige a un défaut de courbure".
B et C sont indépendants.
1. Calculer P( B n C).
P( B n C) = p(B) n P(C) = 0,02 x0,05 =0,001.
2. Calculer la probabilité que la tige ait au moins un défaut.
P(A u B) = p(A)+P(B)-P(A n B) =0,02 +0,05 -0,001 =0,069.
3. Calculer la probabilité que la tige n'ait aucun défaut.
1-P(A u B) =1-0,069 =0,931.

menu