Mathématiques.
Volumes.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
Exercice 1.
Pour fabriquer un puits dans son jardin, Mme
Martin a besoin d’acheter 5 cylindres en béton comme celui décrit
ci-dessous.

Caractéristiques d’un cylindre :
• diamètre intérieur : 90 cm
• diamètre extérieur : 101 cm
• hauteur : 50 cm
• masse volumique du béton : 2 400 kg/m3.
Dans sa remorque, elle a la place pour mettre les 5 cylindres mais elle
ne peut transporter que 500 kg au maximum.
À l’aide des caractéristiques du cylindre, déterminer le nombre minimum
d’allers-retours nécessaires à Mme Martin pour rapporter ses
5 cylindres avec sa remorque.
Volume du cylindre extérieur : 3,14 x1,012 / 4 x0,50 =0,400 m3.
Volume du cylindre intérieur : 3,14 x0,902
/ 4 x0,50 =0,318 m3.
Volume du béton : 0,400-0,318 = 0,0819 m3 ; masse : 0,0819
x2400 ~197 kg.
Elle peut transporter deux cylindres soit 3 allers-retours.
Exercice 2.
Le
gros globe de cristal est un trophée attribué au vainqueur de la coupe
du monde de ski. Ce trophée pèse 9 kg et mesure 46 cm de hauteur.
1. Le biathlète
français Martin Fourcade a remporté le sixième gros globe de cristal de
sa carrière en 2017 à Pyeongchang en Corée du Sud.
Donner approximativement la latitude et la longitude de ce lieu repéré
sur la carte ci-dessous.
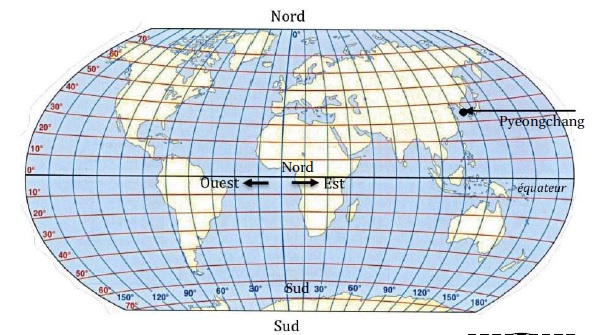
Longitude : 130° Est ; latitude :35° Nord.
2. On considère que ce globe est composé d’un cylindre en
cristal de diamètre 6 cm, surmonté d’une boule de cristal. Montrer
qu’une valeur
approchée du volume de la boule de ce trophée est de 6 371 cm3.
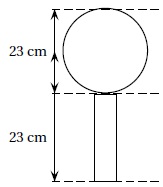
V = 4 / 3 p R3
avec R = 11,5 cm.
V = 4 / 3 x3,14 x11,53 ~ 6 371 cm3.
3. Marie affirme que le volume de la
boule de cristal représente environ 90% du volume total du trophée.
A-t-elle raison ?
Volume du cylindre : pr2h
avec r = 3 cm.
3,14 x 32 x23 ~ 650 cm3.
Volume total : 6371 +650 = 7021 cm3.
La boule représennte 6371 / 7021 ~0,907 ( 90,7 %) du volume total. Elle a raison.
Exercice 3.
Samia vit dans un appartement dont la
surface au sol est de 35 m2.
Elle le compare avec une yourte, l’habitat traditionnel mongol.
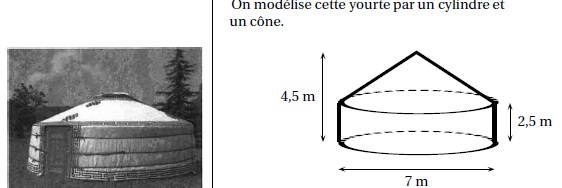
1. Montrer que
l’appartement de Samia offre une plus petite surface au sol que celle
de la yourte.
Aire d'un disque pR2
= 3,14 x3,52 ~38,5 m2, valeur supérieure à 35 m2.
2. Calculer le
volume de la yourte en m2.
Volume du cylindre : p
R2 h = 3,14 x3,52 x2,5 = 96,2 m3.
Volume du cône : p
R2 h / 3= 3,14 x3,52 x2 / 3 = 25,66 m3.
Total : 121,8 ~122 m3.
3.
Sarnia réalise une maquette de cette yourte à l’échelle 1 / 25 .
Quelle est la hauteur de la maquette ?
4,5 / 25 = 0,18 m = 18 cm.
|
Exercice 4.
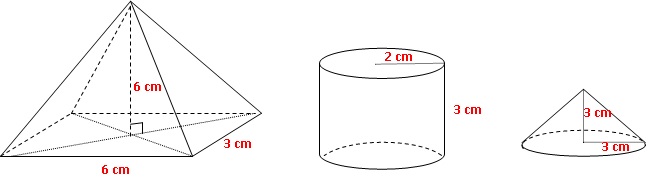
Voici les dimensions de
quatre solides :
- Une pyramide de 6 cm de hauteur dont la base est un rectangle de 6 cm
de longueur et de 3 cm de largeur.
- Un cylindre de 2 cm de rayon et de 3 cm de hauteur.
- Un cône de 3 cm de rayon et de 3 cm de hauteur.
- Une boule de 2 cm de rayon.
1. a) Représenter
approximativement les trois premiers solides.
b) Placer les
dimensions données sur les représentations.
2. Classer ces
quatre solides dans l'ordre croissant de leur volume.
Cône : aire de base x hauteur / 3 = 3,14 x 32 x3 / 3~28,3 cm3.
Boule : 4/3 p r3 = 4 / 3
x3,14 x23 ~33,5 cm3.
Pyramide :
aire de base x hauteur / 3 = 6
x 3 x 6 / 3 =36 cm3.
Cylindre : aire de base x
hauteur = 3,14 x 22 x3 ~37,7 cm3.
Exercice 5.
Afin
de faciliter l’accès à sa piscine, Monsieur Joseph décide de construire
un escalier constitué de deux prismes superposés dont les bases sont
des triangles rectangles.
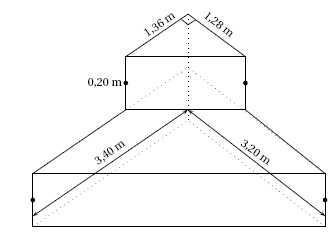
1. Démontrer que le
volume de l’escalier est égal à 1,262 08 m3.
Aire de base du grand prisme : 3,40 x 3,20
/ 2 =5,44 m2 ; hauteur 0,20 m.
Volume du grand prisme : aire de base fois hauteur = 5,44 x0,20 =
1,088 m3.
Aire de base du petit prisme : 1,36 x 1,28
/ 2 =0,8704 m2 ; hauteur 0,20 m.
Volume du petit prisme : aire de base fois hauteur = 0,8704 x0,20
= 0,17408 m3.
Volume total : 1,088 +0,17408=1,262 08 m3.
2.
Sachant que l’escalier est un ouvrage en béton courant, déterminer le
nombre de sacs de ciment de 35 kg nécessaires à la réalisation de
l’escalier.
Un sac de ciment permet d'obtenir 100 L ( 0,100 m3) de
béton.à partir de 5 seaux de sable, 8 seaux de gravillons et 17 L d'eau.
Nombre de sacs de ciment : 1,26208 /0,100 = 12,62 soit 13 sacs de
ciments.
3. Déterminer la
quantité d’eau nécessaire à cet ouvrage.
12,62 x 17 = 214,5
L.
|
Exercice 6.
Romane
souhaite préparer un cocktail pour son anniversaire.

Le récipient choisi par Romane est-il assez grand pour préparer le
cocktail pour 20 personnes ?
Volume du cocktail pour 6 personnes : 60 +30 +12 +12 = 114 cL soit 114
/ 6 = 19 cL par personne.
Volume du cocktail pour 20 personnes : 19 x 20 = 380 cL ou 3,8 L.
Volume du récipient : 2 /3 p
R3 = 2 / 3 x3,14 x133 =4601 cm3 ou 4,6
L.
Le récipient est assez grand.
Exercice
7.
La
gélule est une forme médicamenteuse utilisée quand le médicament
qu’elle contient a une odeur forte ou un goût désagréable que l’on
souhaite cacher. On trouve des gélules de différents calibres. Ces
calibres sont numérotés 000, 00, 0, 1, 2, 3, 4, 5 (« 000 »
désignant le plus grand calibre
et « 5 » désignant le plus
petit). Le tableau suivant donne la longueur
de ces différents calibres de gélule :
Calibre
de la gélule
|
000
|
00
|
0
|
1
|
2
|
3
|
4
|
5
|
Longueur
L de la gélule ( mm)
|
26,1
|
23,3
|
21,7
|
19,4
|
18,0
|
15,9
|
14,3
|
11,1
|
On
considère une gélule constituée de deux demi-sphères identiques de
diamètre 9,5 mm et d’une partie cylindrique d’une hauteur de 16,6 mm.
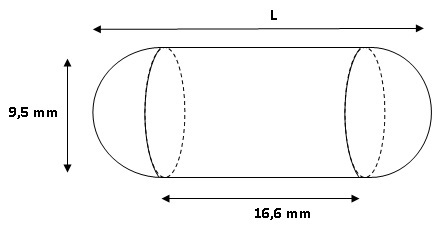
1. À quel calibre
correspond cette gélule ? Justifier votre réponse.
L = longueur du cylindre +
diamètre de la sphère =16,6 + 9,5 = 26,1 mm
( catégorie 000).
2. Calculer le
volume arrondi au mm3 de cette gélule.
Vsphère = 4 /3 p
r3 = 4 / 3 x3,14 x(9,5 / 2)3=448,92
mm3.
Vcylindre = p
r2 h = 3,14 x(9,5 / 2)2x
16,6 =1176,64 mm3.
Vgélule = 448,92 +1176,64 = 1625,56 ~1626 mm3.
3. Robert tombe
malade et son médecin lui prescrit comme traitement une boîte
d’antibiotique conditionné en gélules correspondant au croquis
ci-dessus. Chaque gélule de cet antibiotique a une masse volumique de
6,15 × 10−4 g/mm3. La boîte d’antibiotique
contient 3 plaquettes de 6 gélules. Quelle masse d’antibiotique Robert
a-t-il absorbée durant son traitement ? Donner le résultat en grammes
arrondi à l’unité.
Masse d'une gélule = volume x
masse volumique = 1625,56 x 6,15 10-4
=0,9997 g.
Masse totale des18 gélules ; 18
x 0,9997 = 17,99 ~18 g.
|







