Mathématiques,
DNB
Amérique du Nord 2021.
Durée 2 heures ; noté sur 100 points.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1. Vrai ou faux, justifier. 26 points.
1. On considère la fonction définie par f(x) =3x-7. Faux.
L'image par f du nombre -1 est 2.
f(-1) = 3(-1)-7 = -10.
2. Soit E = (x-5)(x+1).
E a pour forme développée : x2-4x-5. Vrai.
(x-5)(x+1) = x2+x-5x-5 = x2-4x-5.
3. n est un nombre positif.
Lorsque n =5, le nombre 2n+1 est premier. Faux.
25+1 = 32+1 = 33. Ce nombre n'est pas premier. ( ces diviseurs sont 1, 3, 11 et 33).
4. On a lancé 15 fois un dé à six faces non truqué et on a noté les fréquences d'apparition :
Numéro de la face
|
1
|
2
|
3
|
4
|
5
|
6
|
Fréquece d'apparition
|
3 /15
|
4 /15
|
5 /15
|
2 /15
|
1 /15
|
...
|
La fréquence d'apparition du 6 est zéro. Vrai.
La fréquence d'apparition du 6 est notée x / 15.
(3 +4 +5+2+1+x) / 15 =1 = 15 / 15.
15 +x =15 ; x = 0.
5. On considère un triangle RAS rectangle en S.
[AS]=80 cm ; l'agle ARS mesure 26 °.
Le segment [RS] mesure environ 164 cm. Vrai.
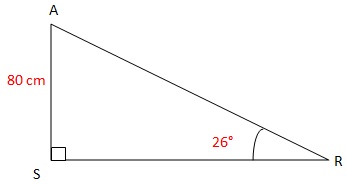
tan 26 = AS / RS ; RS = AS / tan 26 = 80 / tan 26 =164 cm.
Les vecteurs directeurs de ces droites n'étant pas colinéaires, les
droites ne sont pas parallèles.
6. Un rectangle ABCD a pour longueur 160 cm et pour largeur 95 cm.
Les diagonales mesurent exactement 186 cm. Faux.
Diagonale2 = longueur2 + largeur2= 1602 +952 =34625.
Les diagonales mesurent environ 186,077 cm.
Exercice 2. (21 points).
Un athlète a réalisé un triathlon d'une longueur totale de 12,9 km.
Epreuve 1 : natation 400 m ; épreuve 2 : cyclisme ; épreuve 3 : course à pied 2,5 km.
Entre 2 épreuves il doit sur place changer d'équipement.
Le graphe suivant représente la distance parcourue ( km) en fonction du temps ( minute).
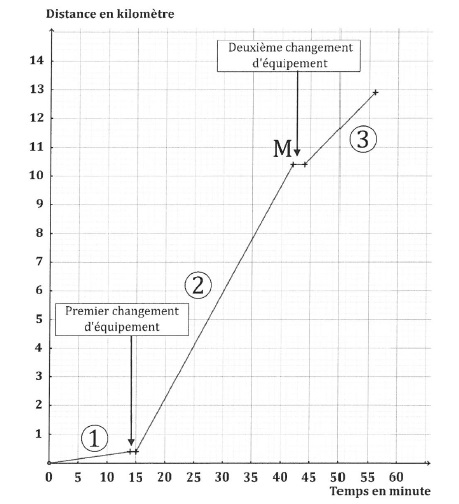
Le point M a pour abscisse 42 et pour ordonnée 10,4.
1. Au bout de combien de temps, l'athlète s'est-elle arrêtée pour effectuer son premier changement d'équipement ?
14 minutes.
2. Quelle est la longueur du parcours de l'épreuve de cyclisme ?
12,9 -0,4 -2,5 =10 km.
3. Quelle est la durée de la course à pied ?
11,5 minutes.
4. Parmi les trois épreuves, pendant laquelle l'athlète a été le moins rapide ?
Epreuve 1 : vitesse = 0,4 / 14 ~0,029 km / min.
Epreuve 2 : vitesse = 10 / 27 ~0,37 km / min.
Epreuve 3 : vitesse =2,5 /11,5 ~0,22 km / min.
L'athlète a été le moins rapide en natation.
5. La vitesse moyenne de l'athlète sur l'ensemble du parcours est-elle supérieure à 14 km / h ?
On considère que les changements d'équipement font partie du triathlon.
distance (km) / durée (minute) = 12,9 / 57 =0,226 km / min soit 0,226 x 60 = 13,6 km / h < 14 km / h.
Exercice 3. 16 points.
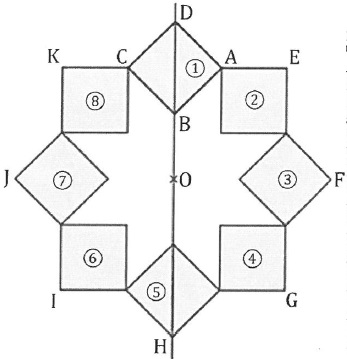
OB = AB. H est le symétrique de D par rapport à O.
La figure a été obtenue en utilisant plusieurs rotations de centre O et d'angle 45°.
La figure est symétrique par rapport à l'axe DB et par rapport au point O.
Pour chacune des affirmations suivantes, indiquer si elle est juste ou
fausse. Justifier.
1. Donner deux carrés différents, images l'un de l'autre par la symétrie axiale d'axe DB.
2 et 8 ; 3 et 7 ; 4 et 6.
2. Le carré 3 est-il l'image du carré 8 par la symétrie centrale de centre O ?
Non, par cette symétrie, l'image de 3 est le carré 7.
3. On considère la rotation de centre O qui transforme le carré 2 en le carré 5. Préciser l'image de [EF] par cette rotation.
[HI].
Exercice 4. 16 points.
On dispose d'un carré partagé en 9 cases blanches de mêmes dimensions.
Quatre instructions permettent de changer l'aspect de certaines cases.
A : case centrale noircie.
B : la case en bas à gauche et en haut à droite sont noircies.
C : la case médiane à gauche et la case médiane à droite sont noircies.
E : inversion des couleurs.
Si une case est déja noire et si l'instruction demande de la noircir, aloors elle reste noire.
On dispose au départ d'un motif dont toutes les cases sont blanches.
1. Représenter le motif obtenu avec la suite d'instruction AB.

2. Quelles ont les deux propositions permettant d'obtenir le motif suivant

ABC ; CE ; BCEC ; CAEA.
3. Donner la suite d'instructions donnant le motif suivant.

ABE.
|
|
....
|
Exercice 5.
On souhaite rénover une salle de nains qui a la forme ci-dessous. Les dimensions sont exprimées en mètres.
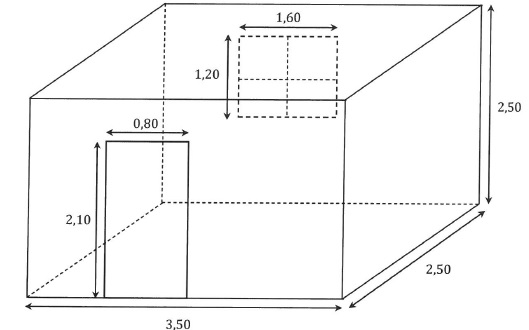
1. Montrer que la surface à recouvrir de papier peint esst de 26,4 m2.
Surface des murs : (3,50 +2,50) x 2,50 x 2 = 30 m2.
Surface de la porte : 2,10 x 0,80 = 1,68 m2.
Surface de la fenètre : 1,6 x1,2 =1,92 m2.
Surface à recouvrir : 30 -1,68 -1,92 =26,4 m2.
2. Calculer le prix en euros, d'un mètre carré de papier peint.
Prix d'un rouleau : 16,95 € ;
surface couverte par un rouleau : 5,3 m2.
Prix d'un mètre carré de papier peint : 16,95 / 5,3 =3,198 ~3,20 .
3. Combien coûtera cette rénovation ?
Conseil du vendeur : prévoir un rouleau supplémentaire pour compenser les pertes liées aux découpes.
Nombre de rouleaux : 1 +26,4 / 5,3 ~ 6.
Prix des rouleaux : 6 x 16,95 =101,7 €.
Prix de deux pôts de colle : 2 x 5,70 =11,4 €.
Total : 101,7 +11,4 =113,1 €.
4. Le jour de l'achat une remise de 8 % est accordée. Quel sera le prix à payer ?
Remise : 113,1 x 0,08 =9,05 €.
prix à payer : 113,1 -9,05 =104,05 €.
.
|
|






