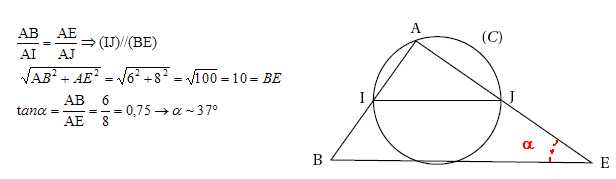Mathématiques.
Thalès, Pythagore.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
Exercice 1.
Un décorateur a dessiné une vue de côté d’un meuble de rangement
composé d’une structure métallique et
de plateaux en bois d’épaisseur 2 cm. Les étages de la structure
métallique de ce meuble de rangement sont tous identiques et la figure
2 représente
l’un d’entre eux.
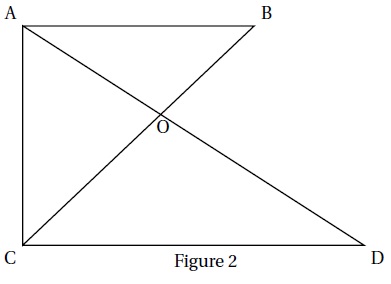
On donne :
• OC = 48 cm; OD = 64 cm; OB = 27 cm; OA = 36 cm et CD = 80 cm;
• les droites (AC) et (CD) sont perpendiculaires.
1. Démontrer que
les droites (AB) et (CD) sont parallèles.
OA / OD = 36 / 64 =9 /16 ; OB / OC = 27 / 48 = 9 / 16.
OA / OD = OB / OC ; les droites (AB) et (CD) sont parallèles.
2.
Montrer par le calcul que AB = 45 cm.
AB / CD= 9 / 16 ; AB = 9 x80 / 16 = 45 cm.
3. Calculer la
hauteur totale du meuble de rangement.
4 étages + 5 épaisseur de bois = 4 AC +5 x 2 = 4 AC +10 cm.
Dans le triangle rectangle ABC : AC2 = BC2 -AB2
=(27+48)2 -452 =3600 ; AC = 60 cm.
Hauteur du meuble : 4 x60 +10 = 250 cm.
Exercice 2.
Michel
participe à un rallye VIT sur un parcours balisé. Le trajet est
représenté en traits pleins. Le départ du rallye est en A et l’arrivée
est en G.
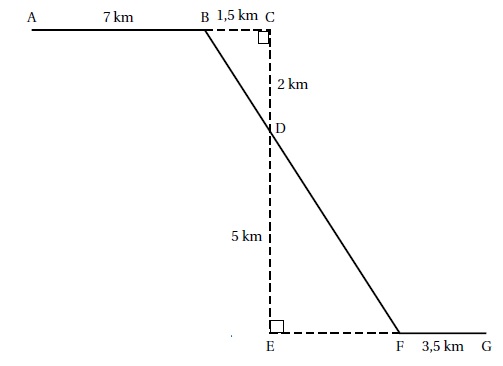
1. Montrer
que la longueur BD est égale à 2,5 km.
Relation de Pythagore dans le triangle rectangle BCD : BD2 =
1,52 +22 =6,25 : BD =2,5 km.
2. Justifier que
les droites (BC) et (EF) sont parallèles.
Les droites (BC) et (EF) sont perpendiculaires à la droite (CE). Les droites (BC) et (EF) sont parallèles.
3.
Calculer la longueur DF.
DF / BD =DE / CD ; DF / 2,5 =5 / 2 = 2,5 ; DF = 2,5 x2,5 =6,25 km.
4. Calculer la
longueur totale du parcours.
AB +BD +DF +FG =7 +2,5 +6,25 +3,5 =19,25 km.
5. Michel roule à
une vitesse moyenne de 16 km/h pour aller du point A au point B.
Combien de temps mettra-t-il pour aller du point A au point B?
Donner votre réponse en minutes et secondes.
7 /16 = 0,4375 heure ou 0,4375 x60 = 26,25 minutes ou 26 min 15 s.
Exercice 3.
Un silo à grains permet de stocker des céréales.
Un ascenseur permet d’acheminer le blé dans le silo.
L’ascenseur est soutenu par un pilier.
On modélise l’installation par la figure ci-dessous qui n’est pas
réalisée à l’échelle :
• Les points C, E et M sont alignés.
• Les points C, F, H et P sont alignés.
• Les droites (EF) et (MH) sont perpendiculaires à la droite (CH).
• CH = 8,50 met CF = 2,50 m.
• Hauteur du cylindre : HM= 20,40 m.
• Diamètre du cylindre : HP = 4,20 m.
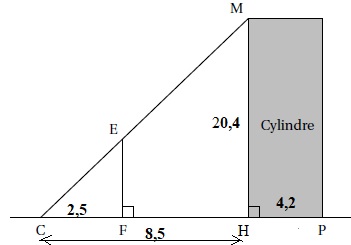
1. Quelle est la
longueur CM de l’ascenseur à blé?
Pythagore dans le triangle rectangle CHM :
CM2 =CH2 +HM2 =8,52+20,42=488,41.
CM = 22,1 m.
2. Quelle est la
hauteur EF du pilier ?
Thalès dans les triangles semblables CEF et CMH :
CH / CF = MH / EF.
8,5 / 2,5 = 20,4 / EF.
EF = 20,4 x2,5 / 8,5 = 6 m.
3. Quelle est la
mesure de l’angleƒ HCM entre le sol et l’ascenseur à blé? On donnera
une valeur approchée au degré près.
tan HCM = MH / CH = 20,4 / 8,5 =2,4. L'angle HCM mesure 67°.
4. Un mètre-cube
de blé pèse environ 800 kg.
Quelle masse maximale de blé peut-on stocker dans ce silo ? On donnera
la réponse à une tonne près.
Volume du cylindre = aire de base fois hauteur =pR2 H =3,14 x2,12
x20,4=282,63 m3.
Masse de blé : 282,63 x0,800 ~ 226
tonnes
|
|
Exercice 4.
.Le triangle ADE a pour dimensions : AD =
7 cm ; AE = 4,2 cm ; DE = 5,6 cm.
AF = 2,5 cm ; AB = AC = 9 cm.
Les droites (FG) et (DE) sont parallèles.
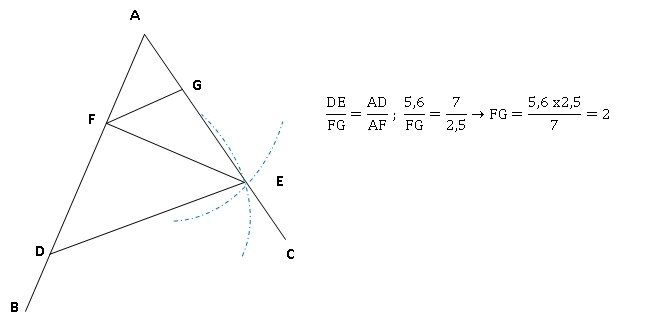
1. Réaliser la
figure en vrai grandeur.
Tracer (AB) ; placer les points B et D sachant que AD = 7 cm et AB = 9
cm.
Pointe du compas en D, tracer un arc de cercle de rayon 5,6 cm.
Pointe du compas en A, tracer un arc de cercle de rayon 4,2 cm.
L'intersection des deux arcs définit le point E.
Tracer AE puis prolonger jusqu'au point C.
Placer le point G.
Tracer DE puis la parrallèle à DE passant par G.
2.
Prouver que le triangle ADE est rectangle en E
AD2 = 49 ; AE2 + DE2
= 4,22 +5,62 =49.
AD2 =AE2 + DE2 ; d'après
la réciproque du théorème de Pythagore, le triangle ADE est rectangle
en E.
3. Calculer FG.
(FG) et (DE) sont parallèles, d'autre part
(AC) et AB) sont sécantes.
A, G, E sont alignés, ainsi que AFD : le théorème de Thalès conduit à
FG = 2 cm. ( voir calcul ci-dessus).
Exercice 5.
On considère la figure
ci-dessous qui n'est pas représentée en waie
grandeur.
Les points A, B et E sont alignés ainsi que les points C, B et D.
Calculer AB dans les trois
cas A, B, C.
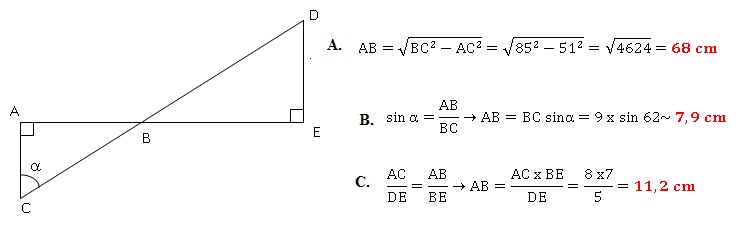
|
Exercice 6.
Dans la figure ci-dessous :
• ABE est un triangle ; AB = 6 cm, AE = 8 cm et BE = 10 cm ;
• I et J sont les milieux respectifs des côtés [AB] et [AE] ;
• le cercle (C) passe par les points I, J et A.
1. Peut-on
affirmer que les droites (IJ) et (BE) sont parallèles ?
2. Montrer que le
triangle ABE est rectangle.
3. Quelle est la
mesure de l’angle AEB ? On donnera une valeur approchée au degré
près.
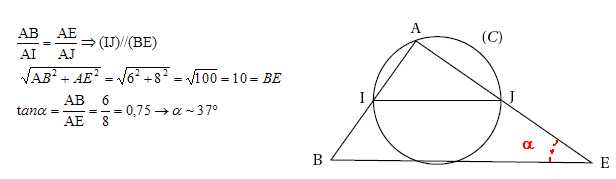
4. a. Justifier que
le centre du cercle (C) est le milieu du segment [IJ].
Le triangle AIJ est rectangle en A et inscrit dans un cercle dont
le diamètre est son hypothénuse IJ.
Le
centre du cercle (C) est le milieu du segment [IJ].
b. Quelle
est la mesure du rayon du cercle (C) ?
IJ = BE / 2 = 5 cm; rayon du cercle R = 2,5 cm.
Exercice
7.
Sur la figure le point J appartient
au segment [IM] et le point K appartient au segment [IL].
Sur la figure, les longueur sont données en mètres.
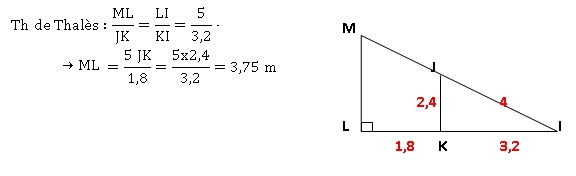
1. Montrer que IKJ
est un triangle rectangle.
IJ2 = 16 ; JK2 + KI2 = 2,42
+3,22 = 16.
IJ2 =JK2
+ KI2 : d'après la réciproque du théorème de
Pythagore, le triangle IJK est rectangle en K.
2.
Montrer que LM est égal à 3,75 m.
(ML) et (JK) sont parallèles, étant toutes
deux perpendiculaires à (IL).
Théorème de Thalès ( IM et IL sont deux sécantes).
3.
Calculer la longueur KM au
centimètre près.
KM2 = ML2 + KL2 = 3,752 +1,82
= 17,30 ; KM = 4,16 m
|