Mathématiques, Brevet Amérique du Sud 2019

Mathématiques, Brevet Amérique du Sud 2019.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.. ..

......

.....

Exercice 1 (20 points)
Pour chacune des affirmations suivantes, indiquer sur la copie, si elle est vraie ou fausse.
On rappelle que chaque réponse doit être justifiée.
• Affirmation n° 1 :
«Dans la série de valeurs ci-dessous, l’étendue est 25. Faux.
Série : 37; 20; 18; 25; 45; 94; 62 ».
Plus grande valeur - plus petite valeur = 94-18=76
• Affirmation n° 2 :
« Les nombres 70 et 90 ont exactement deux diviseurs premiers en commun ». Vrai.
Diviseurs premiers de 70 : 2 ; 5 ; 7.
Diviseurs premiers de 90 : 2 ; 3 ; 5.
• Affirmation n° 3 :
« À partir du quadrilatère BUTS,on a obtenu le quadrilatère VRAC par une translation ». Faux.

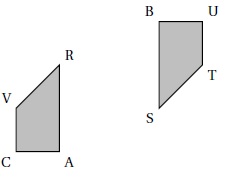
Translation et rotation
• Affirmation n° 4 :
«Quand on multiplie l’arête d’un cube par 3, son volume est multiplié par 27 ». Vrai.
Volume = arête³ .

Exercice 2 13 points
On a saisi dans un tableur les dépenses liées au transport des familles françaises pour les années 2013 et 2015. Ces dépenses sont exprimées en milliards d’euros.
Pour l’année 2013, on a aussi saisi dans ce tableur les dépenses totales annuelles qui correspondent aux dépenses liées au logement, au transport, à la santé, à l’éducation, etc.
Voici une copie de l’écran obtenu.

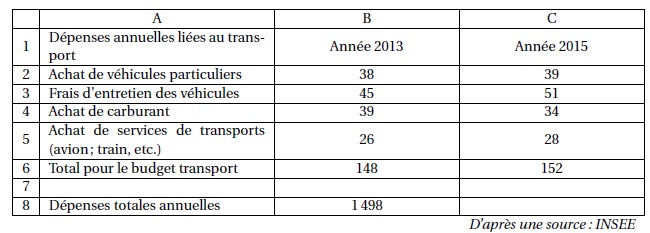
Par exemple : en 2015, les dépenses annuelles des familles françaises, liées à l’achat de carburant, ont été de 34 milliards d’euros.
1. Pour l’année 2015, quelle est la dépense des familles françaises liée aux frais d’entretien des véhicules ?
51 milliards d'euros.
2. Quelle formule peut-on saisir dans la cellule B6 avant de l’étirer dans la cellule C6 ?
=somme(B2:B5)
3. À la lecture du tableau, les dépenses annuelles liées à l’achat de carburant ont-elles baissé de 5% entre 2013 et 2015 ?
Ces dépenses ont baissées de : (39-34) x100 / 34 =14,7 %.
4. En 2015, les dépenses des familles françaises liées aux transports correspondaient à environ 9,87% des dépenses totales annuelles. Quelles étaient alors les dépenses totales annuelles des familles françaises en 2015 ?
152 / 0,0987 = 1540 milliards d'euros..

.. ...

. .
Question 3. (14 points)
1. Calculer 5x² −3(2x +1) pour x = 4.
5 *4²-3(2*4+1)=80-3*9=80-27=53.
2. Montrer que, pour toute valeur de x, on a : 5x² −3(2x +1) = 5x² −6x −3.
5x² −3(2x +1) =5x² −3*2x-3*1=5x² −6x −3.
3. Trouver la valeur de x pour laquelle 5x² −3(2x +1) = 5x² −4x +1.
5x² −6x −3 = 5x² −4x +1.
-6x-3 = -4x+1 ;
-3-1=6x-4x ; -4 = 2x ; x = - 2.

Exercice 4. (23 points).
Un silo à grains permet de stocker des céréales. Un ascenseur permet d’acheminer le blé dans le silo.
L’ascenseur est soutenu par un pilier.
On modélise l’installation par la figure ci-dessous qui n’est pas réalisée à l’échelle :
• Les points C, E et M sont alignés.
• Les points C, F, H et P sont alignés.
• Les droites (EF) et (MH) sont perpendiculaires à la droite (CH).
• CH = 8,50 met CF = 2,50 m.
• Hauteur du cylindre : HM= 20,40 m.
• Diamètre du cylindre : HP = 4,20 m.

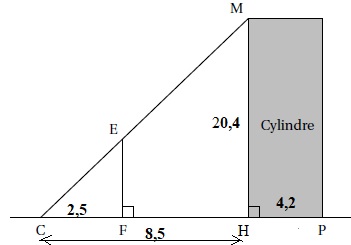
1. Quelle est la longueur CM de l’ascenseur à blé?
Pythagore dans le triangle rectangle CHM :
CM² =CH² +HM² =8,5²+20,4²=488,41. CM = 22,1 m.
2. Quelle est la hauteur EF du pilier ?
Thalès dans les triangles semblables CEF et CMH :
CH / CF = MH / EF.
8,5 / 2,5 = 20,4 / EF.
EF = 20,4 x2,5 / 8,5 = 6 m.
3. Quelle est la mesure de l’angleƒ HCM entre le sol et l’ascenseur à blé? On donnera une valeur approchée au degré près.
tan HCM = MH / CH = 20,4 / 8,5 =2,4. L'angle HCM mesure 67°.
4. Un mètre-cube de blé pèse environ 800 kg.
Quelle masse maximale de blé peut-on stocker dans ce silo ? On donnera la réponse à une tonne près.
Volume du cylindre = aire de base fois hauteur =pR² H =3,14 x2,1² x20,4=282,63 m³.
Masse de blé : 282,63 x0,800 ~ 226 tonnes.

. .

Exercice 5. (14 points)
Une entreprise rembourse à ses employés le coût de leurs déplacements professionnels, quand les employés utilisent leur véhicule personnel.
Pour calculer le montant de ces remboursements, elle utilise la formule et d’équivalence ci-dessous proposés par le gestionnaire :

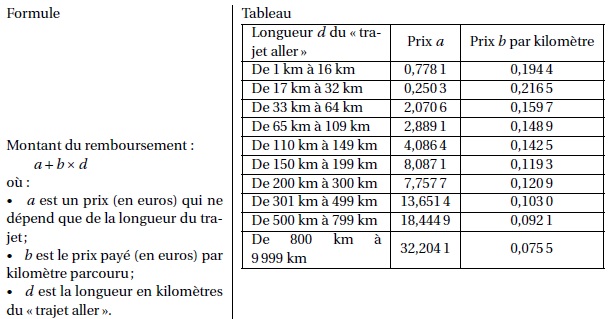
1. Pour un « trajet aller » de 30 km, vérifier que le montant du remboursement est environ 6,75 €.
0,2503 +0,2165 x30 ~ 6,75 €.
2. Dans le cadre de son travail, un employé de cette entreprise effectue un déplacement à Paris. Il choisit de prendre sa voiture et il trouve les informations ci-dessous sur un site internet.
Distance Nantes - Paris : 386 km
Coût du péage entre Nantes et Paris : 37 €
Consommation moyenne de la voiture de l’employé : 6,2 litres d’essence aux 100 km
Prix du litre d’essence : 1,52 €.
Répondre à la question suivante :
« Le montant du remboursement sera-t-il suffisant pour couvrir les dépenses de cet employé pour effectuer le « trajet aller » de Nantes à Paris ? »
Essence : 3,86 x6,2 x1,52 ~ 36,38 €.
Dépense totale : 36,38 +37 =73,38 €.
Remboursement : 13,6514 +0,1030 x386 ~53,41 €.
Les dépenses ne sont pas couvertes.

Question 6. (16 points)
Voici les copies d’écran d’un programme qui permet d’obtenir une frise.

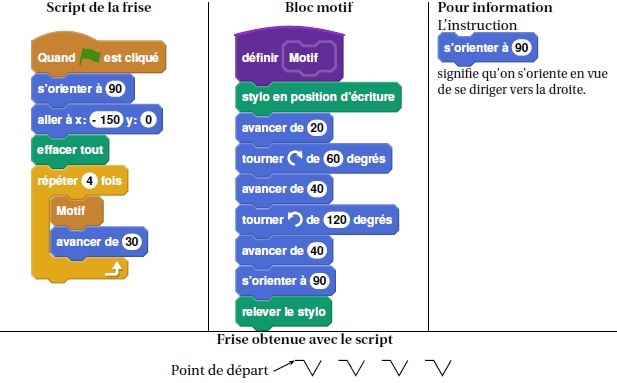
1. Quelle distance le lutin a-t-il parcourue pour tracer un seul motif de la frise ?
20 +40 +40 = 100.
2. On modifie le programme, dans cette question seulement :
• on ne modifie pas le script de la frise.
• dans le bloc motif, il enlève l’instruction : relever le stylo
Dessiner à main levée la frise obtenue avec ce nouveau programme.

3. On utilise maintenant le bloc motif ci-dessous. Laquelle des deux frises obtient-il ? Expliquer pourquoi.

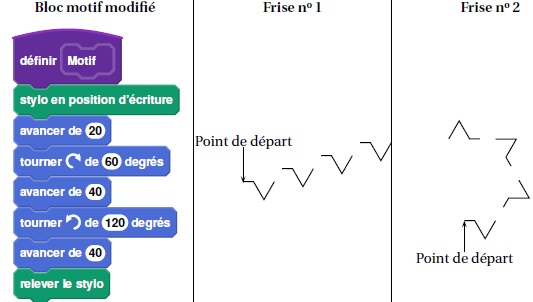
On obtient la frise n°2.
Après une exécution de "motif", on avance de 30 sans changer de direction.
En exécutant une seconde fois "motif", on avance de 20 sans changer de direction.

menu