Mathématiques.
Probabilités.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
Exercice 1.
Dans
la vitrine d’un magasin A sont présentés au total 45 modèles de
chaussures. Certaines sont conçues pour la ville, d’autres pour le
sport et sont de trois couleurs différentes : noire, blanche ou marron.
1. Compléter le
tableau suivant :
Modèle
|
Pour
la ville
|
Pour
le sport
|
Total
|
Noir
|
20-5
= 15
|
5
|
20
|
Blanc
|
7
|
18-5-3=10
|
7+10=17
|
Marron
|
27-7-15
=5
|
3
|
3+5=8
|
Total
|
27
|
45-27=18
|
45
|
2. On
choisit un modèle de chaussures au hasard dans cette vitrine.
a. Quelle est la
probabilité de choisir un modèle de couleur noire ?
20 / 45 = 4 / 9.
b. Quelle est la
probabilité de choisir un modèle pour le sport ?
18 /45 = 2 /5
c. Quelle est la
probabilité de choisir un modèle pour la ville de couleur marron ?
5 /45 = 1 /9.
3. Dans la vitrine
d’un magasin B, on trouve 54 modèles de chaussures dont 30 de couleur
noire.
On choisit au hasard un modèle de chaussures dans la vitrine du magasin
A puis dans celle du magasin B.
Dans laquelle des deux vitrines a-t-on le plus de chance d’obtenir un
modèle de couleur noire ? Justifier.
Dans A, la probabilité d'obtenir une
chausure noire est 4 /9 ;
Dans B, la probabilité d'obtenir une
chausure noire est 30 / 54 =5 /9. Réponse B.
Exercice 2.
Sam préfère les bonbons bleus.
Dans un paquet de 500 bonbons, 150 sont bleus, les autres sont rouges,
jaunes ou verts.
1. Quelle est la
probabilité qu'il pioche un bonbon bleu dans son paquet ?
150 / 500 = 15 / 50 =0,3.
2. 20 % des bonbons
sont rouges. Combien y a t-il de bonbons rouges ?
500 x0,20 = 100.
3. Sachant qu'il y
a 130 bonbons verts dans le paquet, Sam a t-il plus de chance de
piocher au hasard un bonbon vert ou un bonbon jaune ?.
Probabilité de piocher un bonbon vert : 130 /500 = 0,26.
Nombre de bonbons jaunes : 500 -150 -130 -100=120.
Probabilité de piocher un bonbon jaune :
120 /500 = 0,24.
Il a plus de chance de tirer un bonbon vert qu'un bonbon jaune.
4. Aïcha a acheté le même paquet il y a quinze
jours. Il ne lui reste que 140 bonbons bleus, 100 jaunes, 60 rouges et
100 verts. Elle dit à Sam " tu devrais piocher dans mon paquet, plutôt
que dans le tien, tu aurais plus de chance d'obtenir un bleu". A-t-elle
raison ?
Probabilité de piocher un bonbon bleu dans le paquet d'Aïcha :140 /
(140 +100 +60 +100) =140 / 400= 0,35
Probabilité de piocher un bonbon bleu dans
le paquet de Sam :150 / 500 = 0,3.
Aicha a raison.
Exercice 3.
Hugo a téléchargé des titres musicaux sur
son téléphone. Il les a
classés par genre musical comme indiqué dans le tableau ci-dessous :
Genre
musical
|
Pop
|
Rap
|
Techno
|
Variété
française
|
Nombre
de titre
|
35
|
23
|
14
|
28
|
1)
Combien de titres a-t-il téléchargés ?
35+23+14+28=100.
2) Il souhaite
utiliser la fonction « lecture aléatoire » de son téléphone qui
consiste à choisir au hasard parmi tous les titres musicaux
téléchargés, un titre à diffuser. Tous les titres sont différents et
chaque titre a autant de chances d’être choisi. On s’intéresse au genre
musical du premier titre diffusé.
a) Quelle est la
probabilité de l’événement : « Obtenir un titre Pop » ?
35 / 100 = 0,35.
b) Quelle est la
probabilité de l’événement « Le titre diffusé n’est pas du Rap » ?
(100 -23) / 100 = 0,77.
c) Un fichier
musical audio a une taille d’environ 4 Mo (Mégaoctets). Sur le
téléphone d’Hugo, il reste 1,5 Go (Gigaoctet) disponible. Il souhaite
télécharger de nouveaux titres musicaux. Combien peut-il en télécharger
au maximum ?
Rappel : 1 Go = 1 000 Mo.
1500 /4 =375.
|
Exercice 4.
On
considère un jeu constitué d'un plateau tournant et d'une boule. Ce
plateau comporte 13 cases numérotées de 0 à 12. la boule a la même
probabilité de s'arrêter sur chaque case.
1. Quelle est la
probabilité que la boule s'arrête sur la case n° 8 ?
Un seule cas favorables parmi 13 possibilités, donc : 1 / 13 ~0,077.
2. Quelle est la
probabilité que le numéro de la case sur lequel s'arrête la boule soit
un numéro impair ?
Six cas favorables ( 1, 3, 5, 7, 9, 11) sur 13 possibilités, soit 6 / 13 ~0,46.
3. Quelle est la
probabilité que le numéro de la case sur lequel s'arrête la boule soit
un nombre premier ?
Six cas favorables ( 1, 2, 3, 5, 7, 11)
sur 13 possibilités, soit 6 / 13
~0,46.
4. Lors
des deux derniers lancers, la boule s'est arrêtée à chaque fois sur la
case numéro 9. A t-on maintenant plus de chances que la boule s'arrête
sur la case numéro 9 plutôt que sur la case numérotée 7 ? Argumenter.
La boule a la même probabilité de
s'arrêter sur chaque case, quel que soit le résultat des lancers
précédents.
Probabilité d'arrêt sur le numéro 9 = probabilité d'arrêt sur le numéro
7 = 1 / 13. Réponse : non.
Exercice 5.
Deux urnes contiennent des boules
numérotée,s indicsernables au toucher.
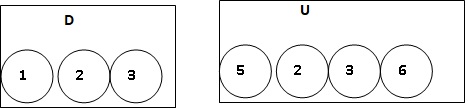
On forme un nombre entier à 2 chiffres en tirant au hasard une boule
dans chaque urne.
Le chiffre des dizaines est le numéro de la boule issue de D. Le chiffre des unités est le numéro de la
boule issue de U.
1. A t-on plus de chances de former
un nombre pair que de former un nombre impair ?
On peut former : 12 ; 13 ; 15 ; 16 ; 22 ; 23 ; 25 ; 26 ; 32 ; 33 ; 35 ;
36.
6 nombres pairs et 6 nombres impairs parmi 12 nombres.
La probabilité de former un nombre pair est égale à celle de former un
nombre impair.
2.a .
Indiquer les nombres premiers que l'on peut former.
13 ; 23 ;
2.b . Montrer que la probabilité
de former un nombre premier est 1 / 6.
2 cas favorables sur 12 cas possibles: 2 / 12 = 1 / 6.
3.
Définir un événement dont la probabilité est 1 / 3.
44 cas favorables sur 12 cas possibles 4 /
12 = 1 / 3.
" Former un nombre qui soit un multiple de 3".
" Obtenir un entier dont la dizaine est 1".
" Obtenir un entier dont la dizaine est 2".
|
Exercice 6.
Partie 1.
On s’intéresse à une course réalisée au début de l’année 2018. Il y a
80 participants, dont 32 femmes et 48 hommes.
Les femmes portent des dossards rouges numérotés de 1 à 32. Les hommes
portent des dossards verts numérotés de 1 à 48.
Il existe donc un dossard n° 1 rouge pour une femme, et un dossard n° 1
vert pour un homme, et ainsi de suite ...
1. Quel est le
pourcentage de femmes participant à la course ?
32 / 80 = 0,4.
2. Un animateur
tire au hasard le dossard d’un participant pour remettre un prix de
consolation.
a. Soit l’évènement V : « Le dossard est vert ». Quelle est la
probabilité de l’évènement V ?
48 / 80 = 0,6.
b. Soit l’évènement
M : « Le numéro du dossard est un multiple de 10 ». Quelle est la
probabilité de l’évènement M ?
Nombre de multiples de 10 : 10 (femmes) ; 10 (hommes) ; 20 ( femmes) ;
20 ( hommes) ; 30 (femmes) ; 30 ( hommes) ; 40 (hommes).
7 / 80.
c. L’animateur
annonce que le numéro du dossard est un multiple de 10. Quelle est
alors la probabilité qu’il appartienne à une femme ?
3 cas favorables sur 7 possibilités : 3 / 7.
Partie 2.
À l’issue de la course, le classement est affiché. On s’intéresse aux
années de naissance des 20 premiers coureurs.
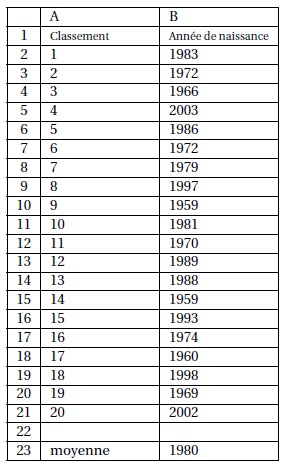
1. On a rangé les
années de naissance des coureurs
dans l’ordre croissant :
1959 1959 1960 1966 1969 1970 1972 1972 1974 1979
1981 1983 1986 1988 1989 1993 1997 1998 2002 2003
Donner la médiane de la série.
La médiane partage la série en deux parties contenant chacune le même
nombre de coureurs soit dix.
La médiane est choisie entre 1979 et 1981, 1980 par exemple.
2. La moyenne de la
série a été calculée dans la cellule B23. Quelle formule a été saisie
dans la cellule B23?
=MOYENNE(B1;B21)
3. Astrid remarque
que la moyenne et la médiane de cette série sont égales.
Est-ce le cas pour n’importe quelle autre série statistique ? Expliquer
votre réponse.
La
moyenne et la médiane ne sont pas
toujours égales.
Soit la série 7 ; 8 ; 12 ; 14 ; 18.
la médiane est la valeur centrale 12.
La moyenne est ( 7 +8 +12 +14 +18) / 5 = 11,8.
Exercice
7.
À un stand
d’une kermesse, on fait tourner une roue pour gagner un lot (un jouet,
une casquette ou des bonbons).
Une flèche permet de désigner le
secteur gagnant sur la roue.
On admet que chaque secteur a autant
de chance d’être désigné.
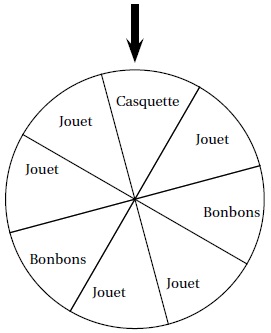
1. a. Quelle est la probabilité de l’évènement « on
gagne des bonbons » ?
2 cas favorables sur 8 cas possibles
: 2 / 8 = 1 / 4 = 0,25.
b. Définir par une phrase l’évènement contraire de
l’évènement « on gagne des bonbons ».
" on gagne un lot qui n'est pas des
bonbons".
" on gagne une casquette ou des
jouets".
c. Quelle est la probabilité de l’évènement défini
au 1. b. ?
1 -0,25 = 0,75.
2. Soit l’évènement « on gagne une casquette ou
des bonbons ».
Quelle est la probabilité de cet
évènement ?
3 cas favorables sur 8 cas possibles
: 3 / 8 = 0,375.
|


