Mathématiques, brevet Polynésie 2020.

Mathématiques, brevet Polynésie 2020.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.. ..

.
.

.. ..
......

...

Exercice 1. 22 points.
Programme de calcul :
Choisir un nombre de départ.
Ajouter 2 à ce nombre.
Elever au carré le résultat.
1. Quel nombre obtient-on si on choisit -7 comme nombre de départ ?
-7+2 = -5 ; (-5)²=25.
2. Développer et réduire l'expression (2x-3)(4x+1).
8x²+2x-12x-3 =8x²-10x-3.
3. Sur la figure suivante, les droites (AB) et (DE) sont parallèles. Les points A, C et D sont alignés. Les points B, C et E sont alignés. Calculer la longueur CB.

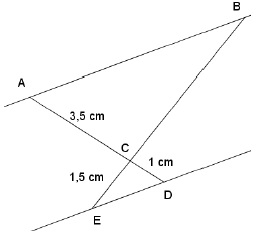
Relation de Thalès : BC / CE = AC / CD ; BC / 1,5 =3,5 / 1 ; BC = 1,5 x 3,5 =5,25 cm.

4. Un article coûte 22 €. Son prix baisse de 15 %. Quel est son nouveau prix ?
100-15 = 85 ; coefficient multiplicateur : 0,85.
22 x 0,85 =18,7 €.

5. On donne les salaires mensuels des employés d'une entreprise. Déterminer le salaire médian et l'étendue des salaires.

Salaire mensuel ( € )
1300
1400
1500
1900
2000
2700
3500

Effectif
11
6
5
3
3
1
1

Effecti total : 30 ; 30 / 2 = 15.
Le salaire médian est le 15^è salaire soit 1400 €.
L'étendue est : 3500-1300=2200 €.

6. Quel est le plus grand nombre premier qui divise 41 895 ?
41 895 = 3 x 3 x 5 x 7 x 7 x19.
Réponse : 19.

Exercice 2. 15 points.
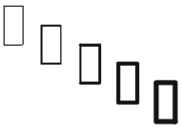
On souhaite réaliser une frise composée de rectangles. On écrit le programme ci-dessous..

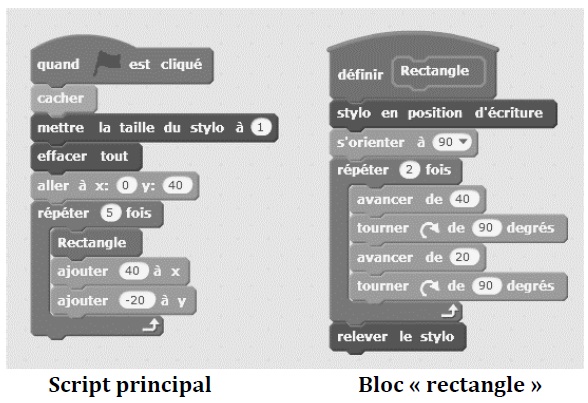
1. Quelles sont les coordonnées du point de départ du tracé ?
x = 0 ; y = 40.
2. Combien de rectangles sont dessinés par le script principal ?
5 rectangles.
3. Dessiner à main levée la figure obtenue avec le script principal.

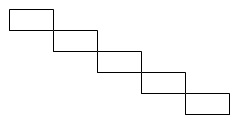
4.a Sans modifier le script principal, on a obtenu la figure ci-dessous composée de rectangle de longueur 40 pixels et de largeur 20 pixels. Proposer une modification du bloc rectangle pour obtenir cette figure.

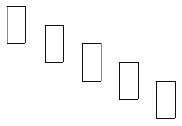
Répéter 2 fois
Avancer de 20.
Tourner de 90° dans le sens des aiguilles d'une montre.
Avancer de 40.
Tourner de 90° dans le sens des aiguilles d'une montre.
Relever le stylo.
b. Où peut-on ajouter l'instruction " Ajouter 1 à la taille du stylo " dans le script principal pour obtenir la figure ci-dessous ?

Rectangle.
Ajouter 40 à x.
Ajouter -20 à y.
Ajouter 1 à la taille du stylo.

.
.

....

Exercice 3. 26 points.
On considère le motif initial suivant :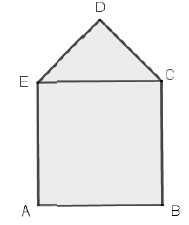
Il est composé d'un carré de côté 5 cm et d'un triangle EDC rectangle et isocèle en D.
Partie 1.
1. Donner sans justification, les mesures des angles DEC et DCE.
45 °.
2. Montrer que le côté [DE] mesure environ 3,5 cm.
DE² +DC² = 2 DE² = EC² ;
DE = EC / racine carrée(2) ~5 / 1,414 ~3,5 cm.
3. Calculer l'aire du motif initial.
Aire du carré + aire du triangle = 5² +3,5 x3,5 / 2 =31,25 ~31 cm².
Partie 2.
On réalise un pavage du plan en partant du motif initial en utilisant diverses transformations.

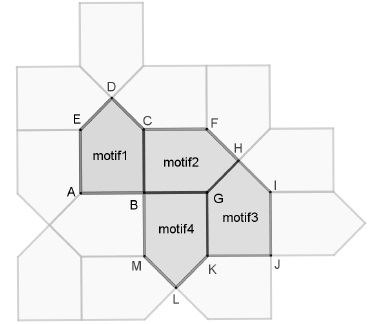
Dans chacun des cas suivants, donner sans justifier une transformation du plan qui permet de passer :
a. Du motif 1 au motif 2.
Rotation de centre B, de 90° dans le sens des aiguilles d'une montre.
b. Du motif 1 au motif 3.
Translation qui transforme B en J, C en I.
c. Du motif 1 au motif 4.
Symétrie de centre B.
d. Du motif 2 au motif 3.
Symétrie par rapport à la droite (GH).

Partie 3.
Suite à un agrandissement de rapport 1,5 de la taille du motif initial, on obtient un motif aggrandi.
1. Construire en vrai grandeur le motif aggrandi.

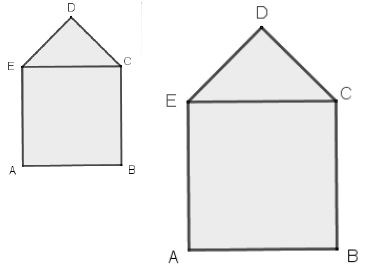
2. Par quel coefficient doit-on multiplier l'aire du motif initial pour obtenir l'aire du motif aggrandi ?
Chaque côté est multiplié par 1,5.
L'aire est donc multipliée par 1,5² = 2,25.

Exercice 4. 16 points.
Jean possède 365 albums de bandes dessinées. Afin de trier les album, il les range par série et classe les séries en trois catégories : franco-belges ( 23 "Astérix" , 33 "tintin", 45 Lucky-Luke" ), comics ( 35 "Batman", 90 " Spider-Man") et mangas ( 85 "One-Piece", 65 " Naturo").
Il choisit un album au hasard.
1. a. Quelle est la probabilié que l'album choisi soit un "Lucky-Luke" ?
45 / 365 =9 / 73 ~0,123.
1. b. Quelle est la probabilié que l'album choisi soit un "comics" ?
(35 + 90) / 365 =125 / 365 = 25 / 73 ~0,342.
1. c. Quelle est la probabilié que l'album choisi ne soit pas un mangas ?
45 / 365 =9 / 73 ~0,123.
(365 -85-65) / 365 =215 / 365 =43 / 73 ~0,59.
2. Tous les albums de chaque série sont numérotés dans l'ordre de sortie en librairie et chacune des séries est complète du numéro 1 au dernier numéro.
a. Quelle est la probabilité que l'album choisi porte le numéro 1 ?
7 séries, donc 7 numéros 1 sur 365 albums.
7 / 365 ~0,019.
b. Quelle est la probabilité que l'album choisi porte le numéro 40 ?
4 séries, donc 4 numéros 40 sur 365 albums.
4 / 365 ~0,011.

Exercice5 . 21 points.
On considère les fonctions f et g suivantes :
f(t) = 4 t+3 ; g(t) =6t.
On donne leurs représentations graphiques.

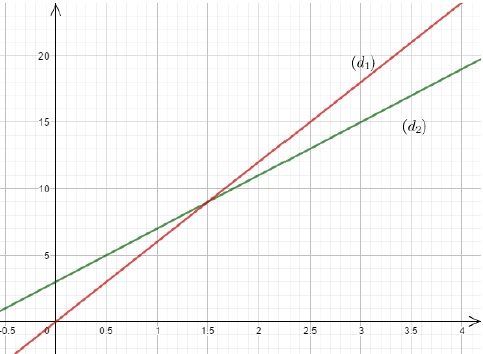
1. Associer chaque droite à sa fonction.
La droite (d₁) passe par l'origine : fonction linéaire g(t) = 6t.
La droite (d₂) ne passe pas par l'origine : fonction affine f(t) = 4t +3.
2. Résoudre par la méthode de votre choix l'équation g(t) = f(t).
6t = 4 t+3 ; 2t = 3 ; t = 1,5.
Coordonnées du point d'intersection des droites : (1,5 ; 9 ).
Camille et Claude décident de faire exactement la même randonnée mais Camille part 45 minutes avant Claude. Camille marche à la vitesse constante de 4 km / h et Claude à 6 km / h.
3. Au moment du départ de Claude, quelle est la distance déja parcourue par Camille ?
45 minutes = 0,75 heure ; 4 x 0,75 = 3 km.
On note t le temps écoulé, ( en heures) depuis le départ de Claude.Ainsi t=0 correspond au moment du départ de Claude.
4. Expliquer pourquoi la distance en km parcourue par Camille en fonction de t peut s'écrire 4t +3.
A la date t=0, Camille a parcouru 3 km puis, chaque heure, il parcourt 4 km.
Distance parcourue par Camille : 4 t +3.
5. Déterminer le temps que mettra Claude pour rattraper Camille.
Distance parcourue par Claude : 6 t.
Date du rattrapage : 4t+3 = 6 t ; t = 1,5 heures = 1 h 30 min.

.

menu