Math�matiques,
DNB septembre 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1. QCM 20 points
1.
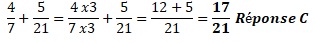
2. Une urne contient 3 boules jaunes, 2 boules bleues et 4 boules vertes, indiscernables au toucher.
On tire une boule au hasard.
Quelle est la probabilit� d’obtenir une boule verte?
Nombre de cas favorables : 4 ; nombre total de boules : 9.
Probabilit� d’obtenir une boule verte = 4 / 9. R�ponse B.
3. Sur quelle figure a-t-on repr�sent� une fl�che et son image par une rotation de centre O et d’angle 90� ?
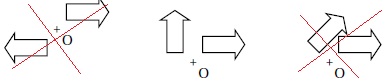
R�ponse B.
4. La d�composition en produit de facteurs premiers de 117 est :
117 = 32 x13. R�ponse A.
5.
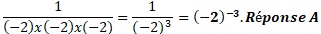
Exercice 2. 20 points.
Sur l’�le deMadagascar, un scientifique m�ne une �tude sur les tortues vertes.
La tortue verte a pour nom scientifique : � Chelonia Mydas �.
La carapace mesure enmoyenne 115 cm et l’animal p�se entre 80 et 130 kg.
Elle est class�e comme esp�ce � En Danger�.
Afin de surveiller la bonne sant� des tortues, elles sont r�guli�rement
pes�es. Voici les donn�es relev�es par ce scientifique enmai 2021.
Lettres de marquage
|
A-001
|
A-002
|
A-003
|
A-004
|
A-005
|
A-006
|
A-007
|
Sexe de la tortue
|
M�le
|
Femelle
|
Femelle
|
Femelle
|
M�le |
Femelle
|
Femelle
|
Masse ( kg)
|
113
|
96
|
125
|
87
|
117
|
104
|
101
|
1. Calculer l’�tendue de cette s�rie statistique.
125 -87 =38.
2. Calculer la masse moyenne de ces 7 tortues. Arrondir le r�sultat � l’unit�.
( 113 +96 +125 +87 +117 +104 +101) / 7 ~106 kg.
3. D�terminer la m�diane de cette s�rie statistique. Interpr�ter le r�sultat.
87 ; 96 ; 101 ; 104 : 113 ; 117 ; 125.
La m�diane est �gale � 104 kg.
La moiti� des tortues p�se moins de 104 kg et l'autre moiti� p�se plus de 104 kg.
4. Est-il vrai que les m�les repr�sentent moins de 20% de cet �chantillon?
Faux ; 2 m�les et 5 femelles soit 2 / 7 ~0,29 ( 29 %).
5. L’�le de Madagascar a pour coordonn�es g�ographiques (200 Sud; 450 Est).
Placer une croix sur le planisph�re fourni en annexe afin de marquer la position de l’�le de Madagascar.
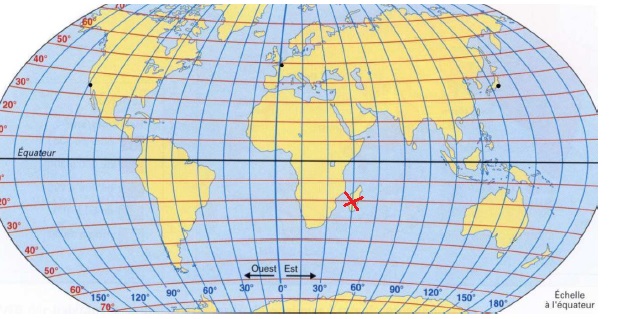
Exercice 3. 20 points.
On consid�re le programme de calcul ci-dessous.
• Choisir un nombre.
• Ajouter 2 � ce nombre.
• Prendre le carr� du r�sultat pr�c�dent.
• Soustraire le carr� du nombre de d�part au r�sultat pr�c�dent.
On a utilis� la feuille de calcul ci-dessous pour appliquer ce programme de calcul au nombre 5; le r�sultat obtenu est 24.
|
A
|
B
|
1
|
Programme
|
R�sultat
|
2
|
Choisir un nombre
|
5
|
3
|
Ajouter 2 � ce nombre
|
7
|
4
|
Prendre le carr� du r�sultat pr�c�dent
|
48
|
5
|
Soustraire le carr� du nombe de d�part au r�sultat prc�dent
|
24
|
1. Pour les questions suivantes, faire appara�tre les calculs sur la copie.
a. Si on choisit 2 comme nombre de d�part, v�rifier qu’on obtient 12 comme r�sultat.
2+2 = 4 ; 42 = 16 : 16-22 = 12.
b. Si on choisit −8 comme nombre de d�part, quel r�sultat obtient-on?
-8+2 = -6 ; (-6)2 = 36 ; 36-(-8)2 =36-64= -28.
2. Parmi les trois propositions suivantes, recopier sur votre copie la formule qui a �t� saisie dans la cellule B5.
=B4 − B2 * B2 ; Vrai.
=B2 + 2 ;
= B3 * B3.
3. a. Si l’on choisit x comme nombre de d�part, exprimer en fonction de x, le r�sultat final de ce programme de calcul.
(x+2)2 -x2.
b. Montrer que (x +2)2 −x2 = 4x +4.
A = x+2 ; B = x ; A2-B2 = (A+B)(A-B).
(2x+2) 2 = 4x+4.
4. Si on choisit un nombre entier au d�part, est-il exact que le r�sultat du programme est toujours un multiple de 4? Justifier.
Vrai : 4x+4) = 4 (x+1), x+1 �tant un entier.
|
|
....
|
Exercice 4. 20 points
Voici trois programmes r�alis�s avec l’application Scratch.
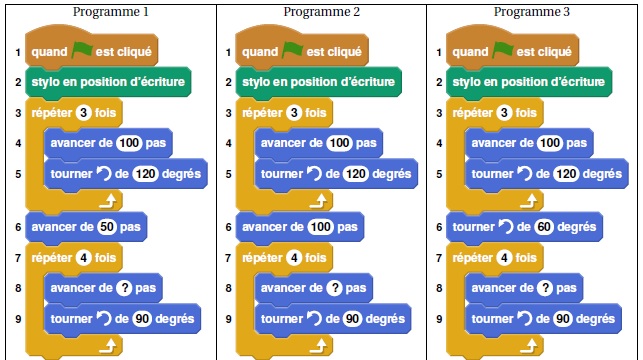
1. Ils donnent les trois figures suivantes constitu�es de triangles et de quadrilat�res identiques.
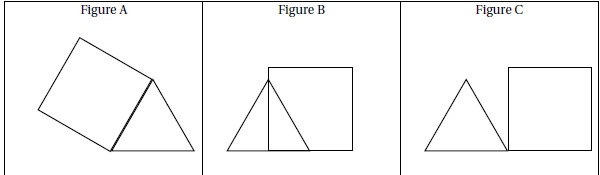
a. Quelle est la nature du triangle et du quadrilat�re sur chaque figure? Aucune justification n’est attendue.
Triangle �quilat�ral ; carr�.
b. Quelle est la valeur manquante � la ligne 8 dans ces 3 programmes ?
A : avancer de 100 pas.
c. Indiquer sur la copie, pour chaque figure, le num�ro du programme qui permet de l’obtenir.
Programme 1 : figure B.
Programme 2 : figure C.
Programme 3 : figure A.
2. a. Maintenant
nous allons modifier les programmes pr�c�dents pour construire d’autres
figures pour lesquelles le p�rim�tre du quadrilat�re est �gal au
p�rim�tre du triangle. Quelle valeur du pas doit-on alors choisir � la
ligne 8 de chaque programme ?
P�rim�tre du carr� : 4 x avex x mesure du c�t� du carr�.
P�rim�tre du triangle �quilat�ral : 3y avec y mesure du c�t� du triangle.
4x = 3y ; x = 0,75 y.
Ligne 8 : avancer de 75 pas.
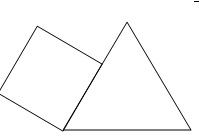
b. Repr�senter la figure A obtenue avec cette nouvelle valeur, en prenant 1 cm pour 25 pas.
Exercice 5. 20 points.
Une famille a achet� une �tag�re qu’elle souhaite placer le long d’un mur.
1. L’�tag�re �tait affich�e au prix de 139,90 €. La famille a obtenu une r�duction de 10 €. Quel a �t� le montant
de cette r�duction ?
10 / 139,90 ~0,071 ( 7,1 %).
2. Voici l’image de profil qu’on peut voir sur le guide demontage de l’�tag�re; ce dessin n’est pas � l’�chelle.
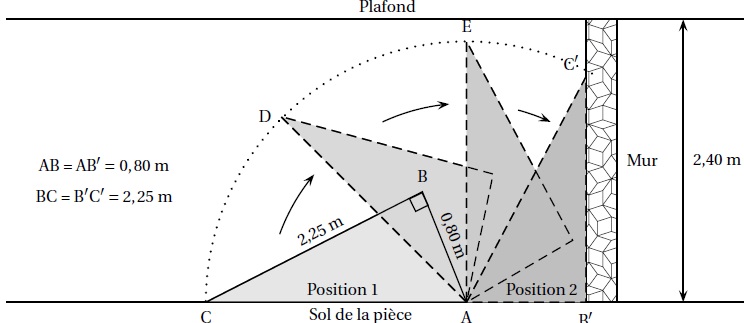
L’�tag�re a �t�mont�e � plat sur le sol de la pi�ce; elle est donc en position 1.
On veut s’assurer qu’elle ne touchera pas le plafond au moment de la relever pour atteindre la position 2.
On ne dispose d’aucun instrument de mesure.
Avec les donn�es du sch�ma pr�c�dent, v�rifier que l’�tag�re ne touchera pas le plafond.
AC2 = BC2 +AB2 =2,252 +0,802 =5,7025.
AC ~2,39 m.
Cette valeur est inf�rieure � 2,40 m, hauteur du plafond.
3. Dans cette question, on supposera que le meuble a pu �tre dispos� contre le mur.
On installe maintenant quatre tablettes horizontales r�guli�rement
espac�es et repr�sent�es ici par les segments [DE], [FG], [HI] et [ JK].
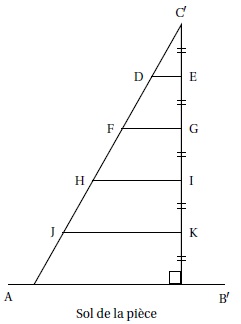
a. Calculer la longueur C′E.
C'E = 2,25 / 5 = 0,45 m.
b. Calculer la longueur de la tablette [DE].
DE / AB' = C'E / C'B'.
DE = C'E x AB' / C'B' = 0,45 x 0,80 / 2,25 = 0,16 m.
c. Calculer la longueur de la tablette [HI].
HI / AB' = C'I / C'B'.
HI = C'I x AB' / C'B' = 3 x 0,45 x 0,80 / 2,25 = 0,48 m.
|
|
