Mathématiques,
brevet Métropole, La Réunion 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice
1. QCM 20 points.
1. On donne la série de nombres suivante :10 ; 6 ; 2 ; 14 ; 25 ; 12 ; 22.
La médiane est :12 ; 13 ; 14.
Ranger les nombres par ordre croissant : 2 ; 6 ; 10 ; 12 ; 14 ; 22 ; 25.
La médiane est le quatrième nombre soit 12.
2.
Un sac opaque contient 50 billes bleues, 45 rouges, 45 vertes et 60
jaunes. Les billes sont indiscernables au toucher. On tire une bille au
hasard dans ce sac. La probabilité que cette bille soit jaune est :60 ;
0,3 ; 1 /60.
60 cas favorables sur 200 possibles ; probabilité de tirer une bille jaune : 60 / 200 = 30 / 100 = 0,3.
3. La décomposition de 2020 en facteurs premiers est :
2 x 10 x101 ; 5 x 5 x101 ; 2 x 2 x 5 x 101.
4. La formule qui permet de calculer le volume d'une boule de rayon R est : 2pR ; pR2 ; 4 / 3 pR3.
5. Une homothésie de centre A et de rapport -2 est une transformation qui :
agrandit les longueurs ; réduit les longueurs ; conserve les longueurs.
Exercice
2. 20 points.
On considère le programme de calcul suivant :.
Choisir un nombre.
Ajouter 7 à ce nombre.
Soustraire 7 au nombre de départ.
Multiplier les deux résultats précédents.
Ajouter 50.
1. Montrer que si le nombre choisi au départ est 2, alors le résultat obtenu est 5.
2+7 =9 ; 2-7=-5 ; -5 x9 = -45 ; -45+50 = 5.
2. Quel est le résultat obtenu si le nombre de départ est -10 ?
-10+7 = -3 ; -10-7=-17 ; -3 x(-17) =51 ; 51 +50 = 101.
3. Un élève
s'aperçoit qu'en calculant le double de 2 en ajoutant 1, il obtient 5,
le même résultat que celui qu'il a obtenu à la question 1.
Il pense que le programme de calcul revient à calculer le double du nombre de départ et à ajouter 1. A-t-il raison ?
-10 x2 = -20 ; -20 +1 = -19 différent de 101. Il a donc tord.
4 Si x est le nombre de départ, montrer que le résultat du programme de calcul est x2+1.
Soit x le nombre de départ :(x+7) (x-7) +50 = x2-49+50 = x2+1.
b. Quel(s) nombre(s) doit-on choisir au départ du programme de calcul pour obtenir 17 comme résultat.
x2+1 =17 ; x2 = 16 ; x = ±4.
Exercice 3. 23 points.
Une entreprise fabrique des portiques pour installer des balancoires sur des aires de jeu.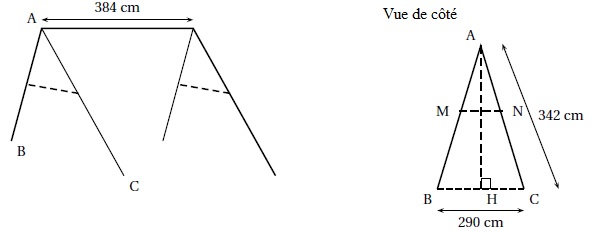
ABC est un triangle isocèle en A. H est le milieu de [BC]. (MN) et (BC) sont parallèles.
1. Déterminer la hauteur AH du portique, arrondie au cm près.
AB2 =AH2+BH2.
AH2 =3422-(290 / 2)2 =95939 ; AH~310 cm.
2. Les barres de maintient doivent être fixées à 165 cm du sommet (AN = 165 cm). Montrer que MN ~140 cm.
Les triangles ABC et AMN sont semblables.
AC / AN = BC / MN ; MN = BC . AN / AC=290 x 165 / 342~140 cm.
3. Montrer que le coût minimal d'un tel portique s'élève à 196,98 €.
Une poutre en bois de diamètre 100 mm, de longueur 4 m : 12,99 €.
4 poutres en bois de diamètre 100 mm, de longueur 3,5 m : 4 x11,75 =47 €.
Deux barres de maintien latérales en bois de longueur 1,5 m :( une barre de 3 m coupée en deux ) 6,99 €.
Ensemble des fixations : 80 €.
Deux balancoires : 50 €.
Total : 196,98 €.
4. L'entreprise veut vendre ce portique équipé 20 % plus cher que son coût minimal. Déterminer ce prix de vente.
196,98 x1,20 = 236,38 €.
5. Pour des raisons de sécurité, l'angle BAC doit être compris entre 45° et 55°. Ce portique respecte t-il cette condition ?
sin BAH = BH / AB = 145 / 342 =0,424 ; l'angle BAH vaut environ 25 °.
L'angle BAC vaut 25 x2 = 50 °. La condition est respectée.
|
|
....
|
Exercice 4. 23 points.
Une association propose diverses activités pour occuper les enfants pendant les vacances. Plusieurs tarifs sont proposés.
Tarif A : 8 € la demi-journée.
Tarif B : une adhésion de 30 € donnant droit à un tarif préférentiel de 5 € par demi-journée.
Un fichier sur tableur a été préparé pour calculer le coût à payer en
fonction du nombre de demi-journées d'activités pour chacun des tarifs.
1. Compléter le tableau.
|
A
|
B
|
C
|
D
|
E
|
F
|
1
|
Nombre de demi-journées
|
1
|
2
|
3
|
4
|
5
|
2
|
Tarif A
|
8
|
16
|
24
|
32
|
40
|
3
|
Tarif B
|
35
|
40
|
45
|
50
|
55
|
2. Retrouver parmi les réponses suivantes la formule qui a été saisie dans la cellule B3 avant de l'étirer vers la droite.
=8*B1 ; =30*B1+5 : =5*B1+30*B1 ; =30+5*B1 ; =35.
3. On considère les fonctions f et g qui donnent les tarifs à payer en fonction du nombre x de demi-journées d'activités.
Tarif A :f(x) = 8 x ; tarif B : g(x) = 30 +5x.
Quelle est celle qui traduit une situation de proportionnalité ?
f(x) = 8 x traduit une situation de proportionnalité.
4. Représenter la fonction f sur le graphique suivant. La fonction g a été représentée.
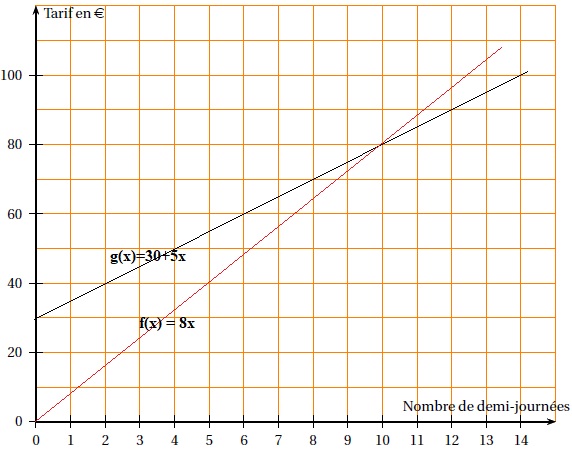
5. Déterminer le nombre de demi-journées d'activités pour lequel le tarif A est égal au terif B.
30+5x = 8x ; 30 = 3x ; x = 10.
6. Avec un budget de 100 €, déterminer le nombre maximal de demi-journées auquelles on peut participer.
Tarif A : 100 / 8 = 12,5 soit 12 demi-journées.
Tarif B : 100-30 = 70 ; 70 / 5 = 14 demi-journées.
Exercice 5. 14 points.
On cherche à dessiner une éolienne avec le logiciel Scratch ; elle est formée de 3 pales qui tournent autour dun axe central.
La figure ci dessous représente une pale.
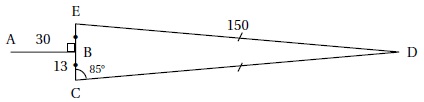
DEC est un triangle isocèle en D ; B est le milieu de [EC] ; [AB] est perpendiculaire à [EC].
1.a Montrer que l'angle ECD est égal à 10°.
Somme des angles d'un triangle : 180° = 85° +85° + angle ECD ; l'angle ECD mesure 10 °.
b. Le script "pale" permet de tracer une pale.
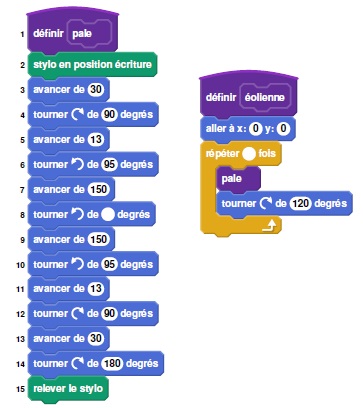
Pourquoi la valeur indiquée dans le bloc de la ligne 6 est-elle 95 ?
180°-85° = 95°.
c. Par quelle valeur doit-on compléter la ligne 8 ?
180-10=170°.
2. Dans le script éolienne, par quelle valeur doit-on compléter la boucle " répéter" ?
Il faut répéter 3 fois la boucle pour dessiner 3 pales.
|
|