Mathématiques.
Fonctions linéaire et affine.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
Exercice 1.
Les représentations graphiques C1 et C2
de deux fonctions sont données dans le repère ci-dessous.
Une de ces deux fonctions est la fonction f définie par f (x) = −2x+8.
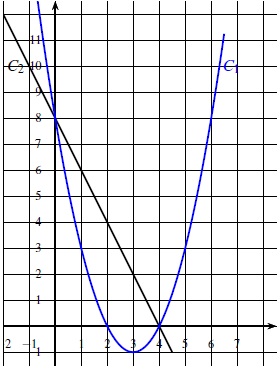
1. Laquelle de ces
deux représentations est celle de la fonction f ?
Le graphe de la fonction affine f est une droite passant par les points
de coordonnées (0 ; 8) et 4 ; 0) : donc C2.
2. Que vaut f (3) ?
f(3) = -2 x3 +8 = 2.
3. Calculer le
nombre qui a pour image 6 par la fonction f .
6 = -2x +8 ; 2x = 8-6 = 2 ; x = 1.
4. La feuille de
calcul ci -dessous permet de calculer des images par la fonction f .
|
A
|
B
|
C
|
D
|
E
|
F
|
|
1
|
x
|
-2
|
-1
|
0
|
1
|
2
|
3
|
2
|
f(x)
|
|
|
|
|
|
|
Quelle formule peut-on saisir dans la cellule B2 avant de l’étirer vers
la droite jusqu’à la cellule G2 ?
= -2*B1+8.
Exercice 2.
1. Développer et réduire
l'expression A.
A = 2x(x-1)-4(x-1) =2x2-2x-4x+4 = 2x2-6x+4.
2. Montrer que -5
est solution de l'équation (2x+1) (x-2) = 63.
[2 (-5) +1] [-5-2] = -9 x (-7) = 63.
3. On considère la
fonction f définie par f(x) = -3x+1,5.
Parmi les graphes ci-dessous, quel est celui qui représente cette
fonction ? Justifier.

Le coefficient directeur de la droite est négatif.
f(0) = 1,5. La droite passe par le point de coordonnées ( 0 ; 1,5).
Donc B.
Exercice 3.
On étudie les performances de deux nageurs
(nageur 1 et nageur 2).
La distance parcourue par le nageur 1 en fonction du temps est donnée
par le graphique ci-dessous.
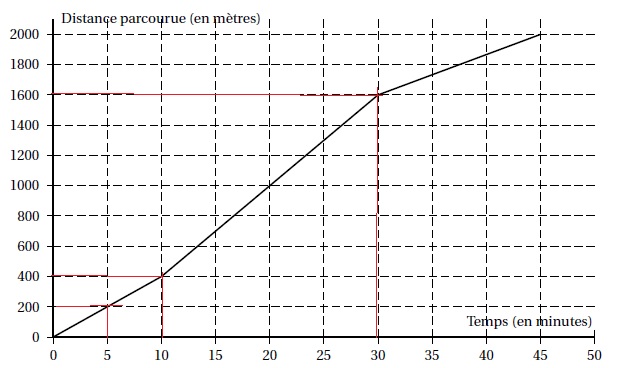
1. Répondre aux
questions suivantes par lecture graphique. Aucune justification n’est
demandée.
a. Quelle est la
distance totale parcourue lors de cette course par le nageur 1?
2000 m.
b. En combien de
temps le nageur 1 a-t-il parcouru les 200 premiers mètres ?
5 minutes.
2. Y a-t-il
proportionnalité entre la distance parcourue et le temps sur l’ensemble
de la course? Justifier.
Non, la courbe n'est pas une droite passant par l'origine.
3. Montrer que la
vitesse moyenne du nageur 1 sur l’ensemble de la course est d’environ
44 m / min.
2000 m parcourus en 45 minutes : 2000 / 45 ~ 44m / min.
4. On suppose
maintenant que le nageur 2 progresse à vitesse constante. La fonction f
définie par f (x) = 50x représente la distance qu’il parcourt en
fonction du temps x.
a. Calculer
l’image de 10 par f .
f(10) = 50 *10 = 500 m.
b. Calculer f (30).
5. Les nageurs 1 et
2 sont partis en même temps,
a. Lequel est en
tête au bout de 10 min? Justifier.
Le nageur 1 a parcouru 400 m en 10 minutes.
Le nageur 2 a parcouru 50 *10 = 500 m en 10 minutes. Celui-ci est
en tête.
b. Lequel est en
tête au bout de 30 min? Justifier.
Le nageur 1 a parcouru 1600 m en 30 minutes.
Le nageur 2 a parcouru 50 *30 = 1500 m en 30 minutes.
Le nageur 1 est en tête.
|
Exercice 4.
Trois
jeunes amis décident de travailler le soir après les cours pour gagner
un peu d’argent. Comme ils ont le permis de conduire, ils s’orientent
vers la livraison de
pizzas. Ils ont réussi à trouver un emploi dans trois pizzerias
différentes.
• David va recevoir un salaire fixe de 70 000 F par mois.
• Guillaume aura un salaire mensuel composé d’une partie fixe de 50 000
F à laquelle s’ajoutent 100 F par livraison effectuée.
• Angelo sera payé chaque mois 200 F par livraison.
1. Si durant un
mois les pizzerias ne reçoivent que très peu de commandes, qui devrait
gagner le plus d’argent ?
David, car il reçoit un salaire fixe, suprérieur à la part fixe des
deux autres..
2. a. Compléter le tableau.
Nombre
de livraisons pr mois
|
50
|
200
|
300
|
600
|
Salaire
de David en F
|
70
000
|
70
000
|
70
000
|
70
000
|
Salaire
de Guillaume en F
|
55
000
|
50
000 +200 x100
=70 000
|
50
000 +300 x100
=80 000 |
50
000 +600 x100
=110 000 |
Salaire
d'Angelo en F
|
50
x200
=10 000
|
200
x 200
=40 000
|
300
x 200
=60 000
|
600
x200
=120 000
|
b.
Durant un mois, combien de livraisons Guillaume doit-il effectuer pour
avoir le même salaire que celui de David ? 200.
3. Dans cette
question, x désigne le nombre de livraisons effectuées durant un mois.
f , g et h sont trois fonctions définies par :
f (x) = 70000 ; g (x) = 200x ; h(x) = 100x +50000.
a. Associer
chacune de ces fonctions à l’un des trois salaires.
f(x) : David ; g(x) : Angelo ; h(x) :: Guillaume.
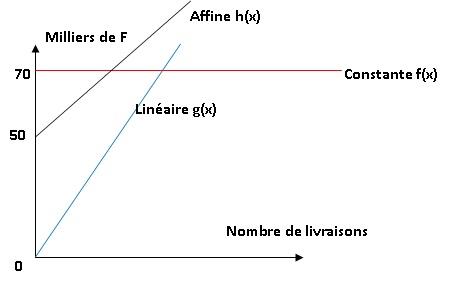
b. Dans le repère
suivant, écrire le nom de la fonction correspondant à chaque droite.
Exercice 5.
Il
existe différentes unités demesure de la température. En France, on
utilise le degré Celsius (°C), aux États-Unis on utilise le degré
Fahrenheit (°F). Voici une représentation de cette correspondance :
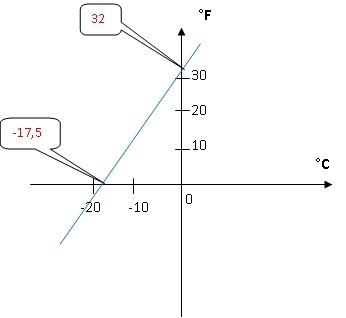
1. En vous appuyant
sur la représentation précédente, déterminer s’il y a proportionnalité
entre la température en degré Celsius et la température en degré
Fahrenheit. Justifier votre réponse.
Il n'y a pas proportionalité entre les degrés Celcius et les degrés
Farhenheit, car le graphe est une droite qui ne passe pas par l'origine.
2. Soit f la
fonction qui à une température x en degré Celsius associe la
température f (x) en degré Fahrenheit correspondante. On propose trois
expressions de f (x) :
Proposition 1 : f (x) = x +32. Proposition 2: f (x) = 1,8x +32.
Proposition 3 : f (x) = 2x +30.
« Les propositions 1 et 3 ne peuvent pas être correctes. C’est donc la
proposition 2 qui convient. ». Justifier cette affirmation.
Pente de la droite : 32 / 17,5 ~1,8 et ordonnée à l'origine : 32.
3. On considère la
fonction f définie par f (x) = 1,8x +32. Calculer f (10) et f (−40).
f(10) =1,8 x10 +32 = 50 ; f(-40)= 1,8 x(-40) +32 = -40.
4.
Existe-t-il une valeur pour laquelle la température exprimée en degré
Celsius est égale à la température exprimée en degré Fahrenheit ?
Justifier votre réponse.
Les températures en degré Celsius et en degré Farhenheit doivent être
égales.
x = 1,8 x +32 ; -0,8 x = 32 ; x = -40.
|
Exercice 6.
Soient
les fonctions f , g et h définies par :
f (x) = 6x ; g (x)= 3x2 −9x
−7 et h(x) = 5x −7.
À l’aide d’un tableur, Pauline
a construit un tableau de valeurs de ces
fonctions.
Elle a étiré vers la droite les
formules qu’elle avait saisies dans les
cellules B2, B3 et B4.
B3
|
=3*B1*B1-9*B1-7
|
|
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
1
|
x
|
-3
|
-2
|
-1
|
0
|
1
|
2
|
3
|
2
|
f(x)=6x
|
-18
|
-12
|
-6
|
0
|
6
|
12
|
18
|
3
|
g(x)
=3x2-9x-7
|
47
|
23
|
5
|
-7
|
-13
|
-13
|
-7
|
4
|
h(x)=5x-7
|
-22
|
-17
|
-12
|
-7
|
-2
|
3
|
8
|
1. Utiliser le
tableur pour déterminer la valeur de h(−2).
h(-2) = -17.
2. Écrire les
calculs montrant que : g (−3) = 47.
3*(-3)*(-3)
-9*(-3)-7=3*9+27-7=47
3. Faire une phrase
avec lemot « antécédent » ou le mot « image » pour traduire l’égalité g
(−3) = 47.
L'image de (-3) par la fonction
g est 47 ; l'antécédent de 47 par la
fonction g est (-3).
4. Quelle formule
Pauline a-t-elle saisie dans la cellule B4 ?
= 5 *B1 -7
5. a. Déduire du
tableau ci-dessus une solution de l’équation : 3x2−9x
−7 =
5x −7.
x=0.
b. Cette équation
a-t-elle une autre solution que celle trouvée grâce au tableur ?
Justifier la réponse.
3x2−9x
−7 -( 5x −7)=0 ; 3x2−9x-5x=0 ; x(3x-14)=0
; solution x = 0 et x = 14 / 3
Exercice
7.
La
copie d’écran ci-dessous montre le travail
effectué par Léa pour étudier trois fonctions f , g et h telles que :
• f (x) = x2+3x −7
• g (x) = 4x +5
• h est une fonction affine dont Léa a oublié d’écrire l’expression
dans la cellule A4.
S=
|
=B1*B1+3B1-7
|
|
A
|
B
|
C
|
D
|
E
|
F
|
1
|
x
|
-2
|
0
|
2
|
4
|
6
|
2
|
f(x)=x2+3x-7
|
-9
|
-7
|
3
|
21
|
47
|
3
|
g(x)=4x+5
|
-3
|
5
|
13
|
21
|
29
|
4
|
h(x)
|
9
|
5
|
1
|
-3
|
-7
|
1.
Donner un nombre qui a pour image −7 par la fonction f .
L'image de 0 par la fonction f est égale à -7..
2. Vérifier à
l’aide d’un calcul détaillé que f (6) = 47.
62+3 x6-7 = 36+18-7=47
3. Expliquer
pourquoi le tableau permet de donner une solution de l’équation :
x2+3x −7 = 4x +5. Quelle est cette solution ?
Dans la partie grisée du tableau rechercher la valeur identique
figurant dans une colonne.
L'antécédent de 21 est 4, solution de l'équation.
4. À l’aide du
tableau, retrouver l’expression algébrique h(x) de la fonction affine h.
h(x) = ax +b avec a et b des constantes.
h(0) = b = 5 ; h(2) =2 a+5=1 d'où a
= -2 ; h(x) = -2x+5.
|




