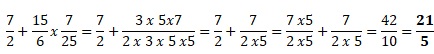Mathématiques, DNB  Centres étrangers 2021. Durée 2 heures ; noté sur 100 points. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Exercice 1.  24 points. 1. Décomposer 360 en produit de facteurs premiers. 360 = 23 x32 x5. 2. 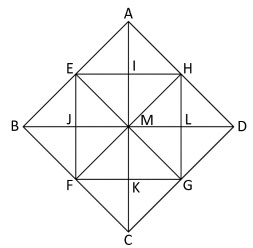A partir du triangle BEJ, rectangle isocèle en J, on a obtenu par pavage la figure suivante : a. Quelle est l'image du triangle BEJ par la symétrie d'axe (BD) ? Triangle BJF. b. Quelle est l'image du triangle AMH par la translation qui transforme le point E en B ? Triangle EFM. c. Par quelle transformation passe t-on du triangle AIH au triangle AMD ? Homothétie de centre A et de rapport 2. 3. Calculer en détaillant. 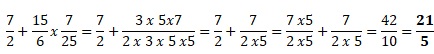4. Sachant que le diamètre de la lune est d'environ 3474 km, la valeur qui approche le mieux son volume est : 12,3 1017 km3 ;  1 456 610 km3 ;  18 1011 km3 ;  2,2 1010 km3 .Vrai. Rayon = R =3474 / 2 = 1737 km Volume V = 4 /3 p R3 =4 / 3 x3,14 x17373~ 2,2 1010 km3 . 5. On considère un triangle RST rectangle en S. Compléter le tableau. ( Arrondir la valeur des angles à l'unité ). 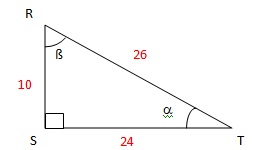tan a = RS / TS = 10 / 24 = 0,417 ; a ~23°. ß = 90-23 ~67°. Périmètre : 10 +24 +26 =60 mm. Aire : RS x ST / 2 = 10 x 24 / 2 = 120 mm2. 6. Un rectangle ABCD a pour longueur 160 cm et pour largeur 95 cm. Les diagonales mesurent exactement 186 cm. Faux. Diagonale2 = longueur2 + largeur2= 1602 +952 =34625. Les diagonales mesurent environ 186,077 cm. Exercice 2. (21 points). Partie 1. On lance un dé équilibré à  6 faces et on note le numéro de la face du dessus. 1. Donner les issues possibles. 1 ; 2 ; 3 ; 4 ; 5 ; 6. 2. Quelle est la probabilité de l'événement A : " on obtient 2". P(A) = 1 / 6. 3. Quelle est la probabilité de l'événement B : " on obtient un nombre impair". 3 cas facorables ( 1 ; 3 ; 5) sur 6 vas possibles. P(B) = 0,5. Partie 2. On lance simultanément 2 dés équilibrés à six faces, un rouge et un vert. On appelle "score" la somme des numéros obtenus sur chaque dé. 1. Quelle est la probabilité de l'événement C " le score est 13" ? Comment qualifie-t-on cet événement ? Le score maximum est 6 +6 = 12. P(C) = 0 ; événement impossible. 2. Dans le tableau à double entrée, on remplit chaque case avec la somme des numéros obtenu sur chaque dé. 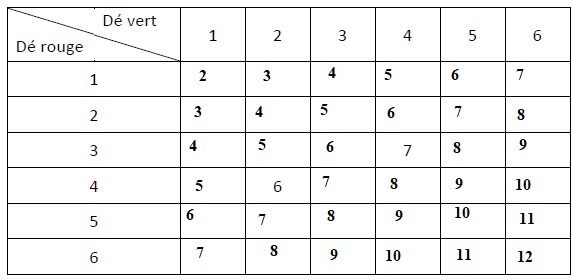Compléter le tableau et donner la liste des scores possibles Scores possibles : 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 ; 10 ; 11 ; 12. 3.a Déterminer la probabilité de l'événement D : le score est 10". 3 cas favorables sur 36 possibles. P(D) = 3 /36 = 1 /12. b. Déterminer la probabilité de l'événement E : le score est un multiple de 4". Multiples de 4 : 4 ; 8 ; 12. 9 cas favorabmes sur 36 possibles. P(E) = 9 / 36 = 0,25. c. Démontrer que le score obtenu a autant de chance d'être un nombre premier qu'un nombre strictement plus grand que 7. Nombres premiers : 2 ; 3 : 5 ; 7 et 11 : 15 possibilités. Nombres strictement supérieurs à 7 : 8 ; 9 ; 10 ; 11 et 12 : 15 possibilités. La probabilité est la même est vaut 15 / 36 = 5 /12. . . .... Exercice 3. (16 points). Un professeur propose à ses élèves trois programmes de calculs, dont 2 sont réalisés avec un logiciel de programmation. 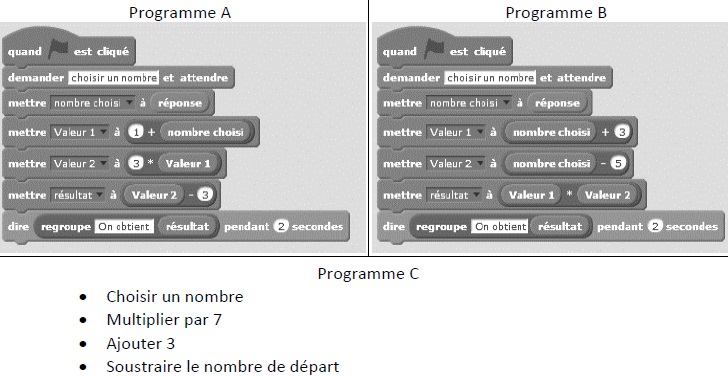1.a Montrer que si on choisit 1 comme nombre de départ, le programme A affiche : on obtient 3. Soit x le nombre initial : résultat = 3 (1+x) -3 =3x ; si x = 1, résultat = 3. b. Montrer que si on choisit 2 comme nombre de départ, le programme B affiche : on obtient -15. Soit x le nombre initial : résultat =  (3+x) (x-5) ; si x = 2, résultat = -15. 2. Soit x le nombre de départ, qu'elle expression obtient-on à la fin de l'éxécution du programme C ? 7x+3-x=6x+3. 3. Un élève affirme qu'avec un des trois programmes on obtient toujours le triple du nombre choisi. A-t-il raison ? A : résultat = 3(1+x-1) =3x. Vrai. B : résultat = (3+x) (x-5) C : résultat = 3(2x+1). 4.a Résoudre (x+3)(x-5) =0. x+3 = 0 soit x = -3. x-5=0 soit x = 5. b. Pour quelles valeurs de départ le programme B affiche-t-il zéro ? B affiche zéro si le nombre de départ est 5 ou -3. 5. Pour quelle(s) valeur(s) de départ le programme C affiche-t-il le même résultat que le programme A ? 3x=6x+3 ; 3x+3=0 ; x =-1. Exercice 4. 19 points. Aurélie est partie de l'altitude 251 m et arrive au sommet du col à l'altitude 393 m. 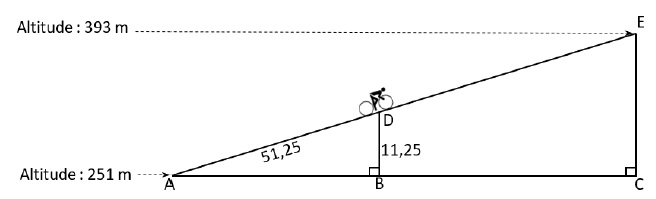Les droites (AB) et (DB) sont perpendiculaires. Les droites (AC) et (CE) sont perpendiculaires. Les points A, D et E sont alignés. Les points A, B et C sont alignés. AD = 51,25 m ; DB = 11,25 m. 1. Justifier que CE = 142 m. EC =393 -251 = 142 m. 2.a. Montrer que les droites (DB) et (EC) sont parallèles. Les droites (DB) et (EC) étant toutes deux perpendiculaires à la droite (AC), elles sont donc parallèles. b. Montrer que DE ~596 m. Les triangles ADB et AEC sont semblables :  EC / DB = AE / AD. AE = EC x AD / DB = 142 x 51,25 / 11,25 =648,9. DE = AE -AD = 648,9 - 51,25 =595,6 ~596 m. 3. Aurélie roule à une vitesse moyenne de 8 km / h ; si elle part à 9h55 du point D, à quelle heure arrivera-t-elle au point E ? 8 /3,6 ~2,222 m /s. 596 /2,222 =268 s ou 4,47 min environ 4 min 28 s. 4. La pente d'une route se calcule de la manière suivante : pente = dénivelé / longueur horizontale  parcourue. Montrer que la pente de cette route est de 22 %. Pente = BD / AB. AB2 = AD2-BD2 =51,252 -11,252 = 2500 ; AB = 50 m. 11,25 / 50 =0,225  ( 22,5 %). Exercice 5. (20 points). Une station de ski propose à ses clients trois formules pour la saison d'hiver. A : 36,50 € par jour de ski. B : abonnement 90 € pour la saison + 18,50 € par jour de ski.( ski plus). C : 448,50 € pour toute la saison ( ski total). 1. Compléter le tableau suivant : Nombre de jours de ski 2 6 10 Formule A 73 36,5 x6=219 365 Formule B 127 90+6 x18,5=201 90+185=275 Formule C 448,50 448,50 448,50 2.  On désigne par x le nombre de jours de ski. f(x) = 90 +18,5 x ; g(x) = 448,5 ; h(x) = 36,5 x. a. La quelle des trois représente une relation de proportionnalité ? h(x) = 36,5 x. b. Associer chaque fonction aux formules A, B, C. A : h(x) ; B : f(x) ; C : g(x). c. Calculer le nombre de jours de ski pour lequel le montant à payer avec les formules A et B est identique. 36,5 x = 90+18,5 x. 18x=90 ; x =90 / 18 = 5. 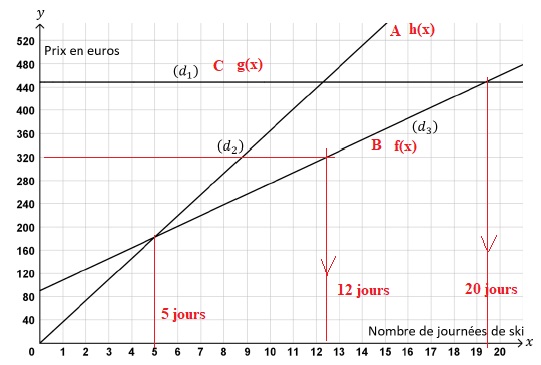3. On a représenté graphiquement les trois fonctions. a. Associer à chaque droite la bonne fonction. b. Avec un budget de 320 €, pendant combien de jour peut-on skier ?.  A partir de combien de jours de ski, la formule C est-elle la plus avantageuse ?

menu