Mathématiques,
DNB Asie Pacifique 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1 24 points
Pour chacun des six énoncés suivants, écrire sur la copie le numéro de la question et la réponse choisie.
Il ya une seule réponse correcte par énoncé.
On rappelle que toutes les réponses doivent être justifiées.
1) Le nombre 126 a pour diviseur 252 ; 20 ; 6 vrai.
126 / 6 = 21.
2) On considère la fonction f définie par : f (x) = x2 −2.
L’image de 2 par f est -2. Faux. f(2) = 22-2 = 2.
f(-2) =0. Faux. f(-2) = (-2)2-2 =4-2= 2.
f(0) = -2. Vrai. f(0) = 02-2 = - 2.
3) Dans la cellule A2 du tableur ci-dessous, on a saisi la formule
= −5*A1*A1+2*A1−14
puis on l’a étirée vers la droite.
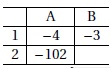
Quel nombre obtient-on dans la cellule B2 ? -65 vrai ; 205 ; 25.
-5 x(-3)2+2x(-3)-14= -45-6-14= -65
4) Les solutions de l’équation x2 = 16 sont . . .
-8 et 8 ; -4 et 4 vrai ; -32 et 32.
x = ± racine carrée (16).
5) 2×2400 est égal à . . .2401 vrai ; 4400 ; 2800.
2(400+1) = 2401.
6) La largeur et la hauteur d’une télévision suivent le ratio 16 : 9. Sachant que la hauteur de cette télévision
est de 54 cm, combien mesure sa largeur ?
94 cm ; 96 cm vrai ; 30,375 cm .
L / h = 16 / 9.
Si h = 54 cm, L = 54 x16 / 9 = 96 cm.
54 / 16 x 9 =30,375 cm.
Exercice 2 (21
points)
Le quadrilatère ABCD est un carré de côté de longueur 1 cm. Il est noté carré ①.
Les points A, B, E et H sont alignés, ainsi que les points A, D, G et J.
On construit ainsi une suite de carrés (carré ① carré ②, carré ③, . . .
) en doublant la longueur du côté du carré, comme illustré ci-dessous
pour les trois premiers carrés.
La figure n’est pas en vraie grandeur.
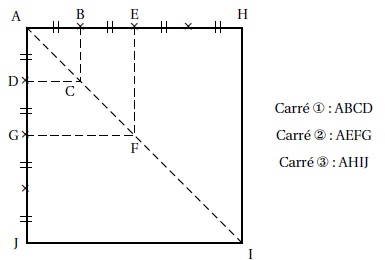
1. Calculer la longueur AC.
Diagonale du carré de côté1 : AC = racine carrée (2) = 2½ ~1,414 cm.
2. On choisit un carré de cette suite de carrés.
Aucune justification n’est demandée pour les questions 2. a. et 2. b.
a. Quel coefficient d’agrandissement des longueurs permet de passer de ce carré au carré suivant ?
Coefficient :multiplié par 2.
b. Quel type de transformation permet de passer de ce carré au carré suivant ?
symétrie axiale, homothétie, rotation, symétrie centrale, translation.
Homothétie de centre A et de rapport 2.
c. L’affirmation «
la longueur de la diagonale du carré ③ est trois fois plus grande que
la longueur de la diagonale du carré ①» est-elle correcte ?
Faux : AI = 2 AF = 4 AC.
3. Déterminer, à l’aide de la calculatrice, une valeur approchée de la mesure de l’angle AJB au degré près.
tan ( AJB) = AB / AJ = 1 / 4 = 0,25 ; mesure de cet angle : ~14°.
Exercice 3 (21
points)
Voici un algorithme :
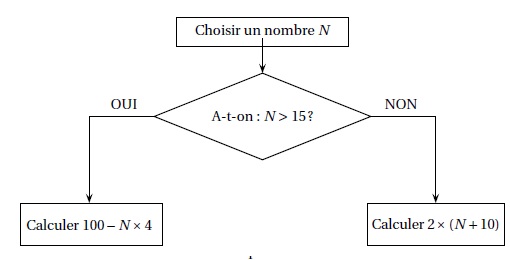
1. Justifier que si on choisit le nombre N de départ égal à 18, le résultat final de cet algorithme est 28.
18 >15 oui.
100-18 x 4 = 28.
2. Quel résultat final obtient-on si on choisit 14 comme nombre N de départ ?
14 < 15.
2x(14+10) =48.
3. En
appliquant cet algorithme, deux nombres de départ différents permettent
d’obtenir 32 comme résultat final. Quels sont ces deux nombres ?
Soient x et y ces deux nombres.
x > 15 : résultat :100-4x = 32.
4x = 100-32 ; x = 68 / 4 ; x = 17.
y < 15 : résultat : 2(y+10)=32.
2y +20 = 32.
2y = 12 ; y = 6.
4. On programme l’algorithme précédent :
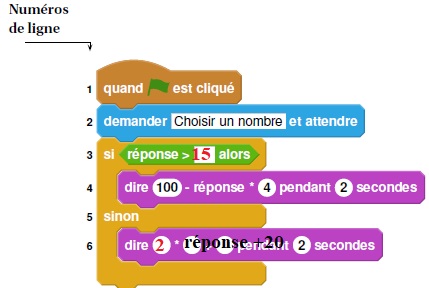
a. Recopier la ligne 3 en complétant les pointillés :
ligne 3 : si réponse > 15 alors
b. Recopier la ligne 6 en complétant les pointillés :
ligne 6 : dire 2*(réponse +10) pendant 2 secondes.
5. On choisit au hasard un nombre premier entre 10 et 25 comme nombre N de départ.
Quelle est la probabilité que l’algorithme renvoie un multiple de 4 comme résultat final ?
Nombres premiers possibles :11 ; 13 ; 17 ; 19 ; 23.
N = 11 : résultat : 2(11+10)=42 ; ce n'est pas un multiple de 4.
N = 13 : résultat : 2(13+10)=46 ; ce n'est pas un multiple de 4.
N = 17 : résultat :100 -4 *17 = 32, multiple de 4.
N = 19 : résultat :100 -4 *19 = 24, multiple de 4.
N = 23 : résultat :100 -4 *23 = 8, multiple de 4.
3 possibilités sur 5 ; la probabilité d'obtenir un multiple de 4 est 3 / 5 = 0,6.
|
|
....
|
Exercice 4 (16 points)
En cours d’éducation physique et sportive (EPS), les 24 élèves d’une classe de troisième pratiquent la course de fond.
Les élèves réalisent le test de demi-Cooper : ils doivent parcourir la plus grande distance possible en six minutes.
Chaque élève calcule ensuite sa vitesse moyenne sur cette course. Le résultat obtenu est appelé VMA
(Vitesse Maximale Aérobie).
1. Après son échauffement, Chloé effectue ce test de demi-Cooper, Elle parcourt 1 000 mètres en 6 minutes.
Montrer que sa VMA est égale à 10 km/h.
1000 m = 1 km ; 6 minutes = 6 / 60 = 0,1 heure.
Vitesse moyenne = distance / durée = 1 / 0,1 = 10 km /h.
2. L’enseignante a récolté les résultats et a obtenu les documents 1 et 2 ci-dessous :
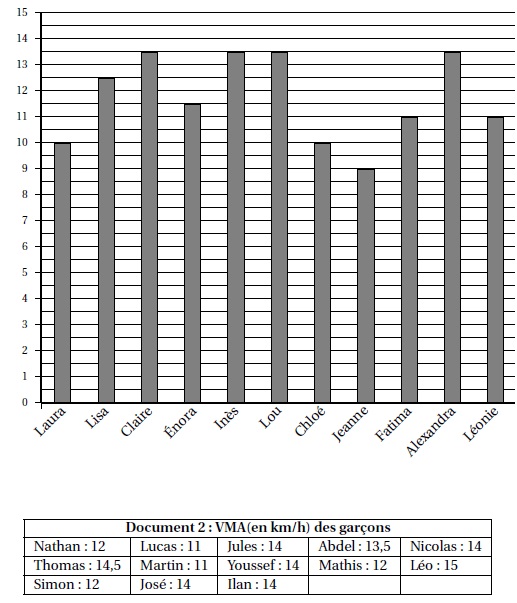
Dire si les affirmations suivantes sont vraies ou fausses. On rappelle que toutes les réponses doivent être justifiées.
a. Affirmation 1 :
l’étendue de la série statistique des VMA des filles de la classe est
plus élevée que celle de la série statistique de VMA des garçons de la
classe. Vrai.
Filles : 13,5-8=9 = 4,5 km / h.
Garçons : 15-11 = 4 km / h.
b. Affirmation 2 : plus de 25% des élèves de la classe a une VMA inférieure ou égale à 11,5 km/h. Vrai.
6 filles et 2 garçons soit 8 élèves sur 24.
8 / 24 ~ 0,33 ( 33 %)
c. L’enseignante
souhaite que la moitié de la classe participe à une compétition. Elle
sélectionne donc les douze élèves dont la VMA est la plus élevée.
Affirmation 3 : Lisa participe à la compétition. Faux.
12 élèves ont une VMA strictement supérieure à 12,5. Lisa ( VMA = 12,5 ) ne participe pas à la compétition.
Exercice 5 (16
points)
Première partie.
En plaçant plusieurs cubes unités, on construit ce solide :
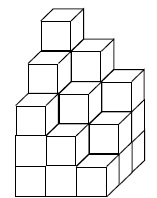
Question : Combien de cubes unités au minimum manque-t-il pour compléter ce solide et obtenir un pavé droit ?
Rangée 2, il manque un cube.
Rangée 3, il manque 3 cubes.
Rangée 3, il manque 9-3=6 cubes.
Rangée 4, il manque 9-1=8 cubes.
Total : 1+3+6+8=18 cubes.
Partie 2.
Un jeu en 3D contient les sept pièces représentées ci-dessous. Chaque pièce est constituée de cubes identiques d’arête 1 dm.
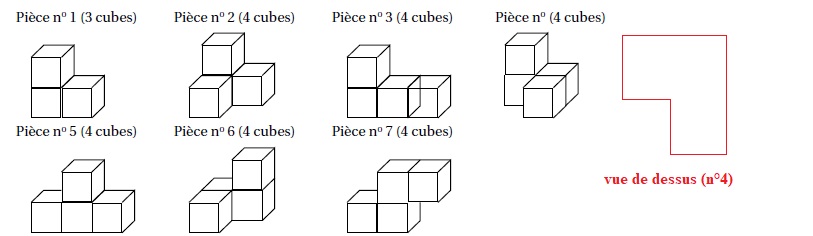
1. Dessiner une vue de dessus de la pièce n° 4 (en prenant 2 cm sur le dessin pour représenter 1 dm dans la réalité).
2. À l’aide de la totalité de ces sept pièces, il est possible de construire un grand cube sans espace vide.
a. Quel sera alors le volume en dm3 de ce grand cube ?
27 petits cubes unités ( 1 dm3) soit 27 dm3.
b. Quelle est la longueur d’une arête (en dm) de ce grand cube?
Chaque rangée compte 9 cubes soit une arète de 3 dm.
|
|