Mathématiques.
Aires.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
Exercice 1.
Monsieur
Chapuis souhaite changer le carrelage et les plinthes(*) dans
le salon de son appartement. Pour cela il doit acheter des carreaux, de
la colle et des plinthes en bois qui seront clouées. Il dispose des
documents suivants :
Document 1
: plan , la
pièce correspond à la partie grisée.
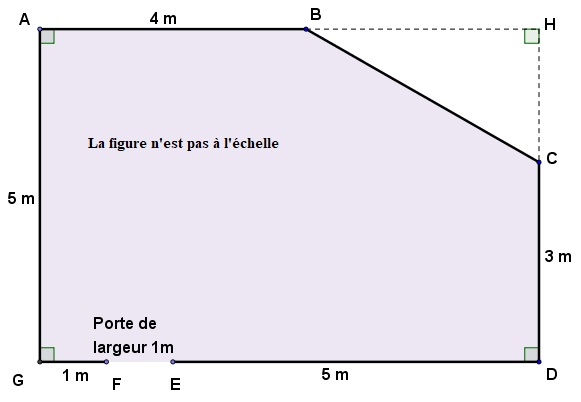
1. a. En
remarquant que
la longueur GD est égale à 7 m, déterminer l’aire du triangle BCH.
BH x HC / 2 = 3 x2 / 2 = 3 m2.
b. Montrer que
l’aire de la pièce
est 32 m2.
Aire du rectangle AHDG - aire du triangle BCH= 7 x5 -3 =32 m2.
2. Pour ne pas
manquer de carrelage
ni de colle, le vendeur conseille à
monsieur Chapuis de prévoir une aire supérieure de 10 % à l’aire
calculée à la question 1.
Monsieur
Chapuis doit
acheter des boîtes entières et des sacs entiers.
Déterminer
le nombre de
boîtes de carrelage et le nombre de sacs de colle à acheter.
32 x1,1 =35,2 m2.
Un sac de colle permet de coller 4 m2, il faut donc 9 sacs.
Une boîte de carreaux permet de couvrir 1,25 m2, donc il
faut 35,2 / 1,25 ~28 boîtes.
3. Le vendeur
recommande aussi de
prendre une marge de 10% sur la
longueur des plinthes. Déterminer le nombre total de plinthes que
monsieur Chapuis doit acheter pour faire le tour de la pièce. On
précise qu’il n’y a pas de plinthe sur la porte.
BC2 =BH2 + HC2 =32+22=13
; BC ~3,6 m.
Longueur des plintes :5 +1 +5 +4 +3 +3,6 = 21,6 m.
Puis prendre en compte la marge : 21,6 x1,1 ~23,8 m.
Longueur d'une plinthe : 1m ; il faut donc 24 plinthes.
4. Quel est le
montant de la dépense
de monsieur Chapuis, sachant qu’il
peut se contenter d’un paquet de clous ? Arrondir la réponse à l’euro
près.
Carrelage 19,95 € la boîte soit 19,95 x28 =558,6 €
Colle, 22 € le sac soit 22 x9 = 198 €.
Plinthe, 2,95 € le mètre, soit 2,95 x24 =70,8 €.
Clous, 5,50 €.
Total : 832,9 €.
Exercice 2.
La figure PRC ci-dessous représente un
terrain appartenant à une
commune.
Les points P, A et R sont
alignés. Les points P, S et C sont alignés.
Il est prévu d’aménager
sur ce terrain :
• une « zone de jeux pour
enfants » sur la partie PAS ;
• un « skatepark » sur la
partie RASC.
On connaît les dimensions
suivantes : PA = 30 m; AR = 10 m; AS = 18 m.
1.
La commune souhaite semer du gazon sur la « zone de jeux pour enfants
». Elle décide d’acheter des sacs de 5 kg de mélange de graines pour
gazon à 13,90 € l’unité. Chaque sac permet de couvrir une surface
d’environ 140 m2.
Quel budget doit prévoir
cette commune pour pouvoir semer du gazon sur
la totalité de la « zone de jeux pour enfants » ?
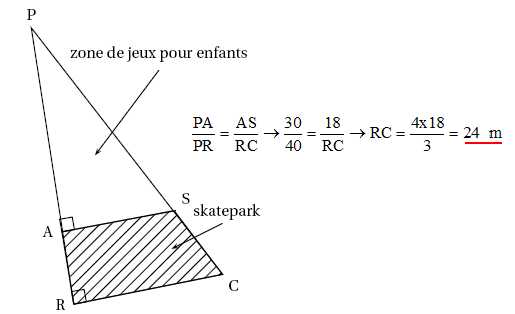 Aire de la zone de jeu (
triangle rectangle en A) : PA *AS / 2 = 30 x
18 /2 = 270 m2.
Nombre de sacs : 270 /
140 = 1,93 soit 2 sacs.
Coût : 2 x13,90 = 27,8 €.
2. Calculer l’aire
du « skatepark »
Aire du triangle PRC
rectangle en R : PR * RC / 2 = 40 x24 / 2 = 480 m2.
Aire du skatepark : 480 -
270 = 210 m2.
Aire de la zone de jeu (
triangle rectangle en A) : PA *AS / 2 = 30 x
18 /2 = 270 m2.
Nombre de sacs : 270 /
140 = 1,93 soit 2 sacs.
Coût : 2 x13,90 = 27,8 €.
2. Calculer l’aire
du « skatepark »
Aire du triangle PRC
rectangle en R : PR * RC / 2 = 40 x24 / 2 = 480 m2.
Aire du skatepark : 480 -
270 = 210 m2.
Exercice 3.
Une
pizzeria fabrique des pizzas rondes de 34 cm de diamètre et des
pizzas carrées de 34 cm de côté.
Toutes les pizzas ont lamême épaisseur et sont livrées dans des boîtes
identiques.
Les pizzas carrées coûtent 1 € de plus que les pizzas rondes.
1. Pierre achète
deux pizzas : une ronde et une carrée. Il paye 14,20 €. Quel est le
prix de chaque pizza ?
x : prix d'une pizza ronde ; x +x+1 = 14,20 ; 2x = 13,20 ; x = 13,20 /
2 = 6,60 €.
2. Les pizzas
rondes sont découpées en huit parts de même taille et les pizzas
carrées en neuf parts de même taille.
Dans quelle pizza trouve-t-on les parts les plus grandes ?
Aire d'une pizza ronde : pr2
=3,14 x172~ 908 cm2 ; aire d'une part : 908
/ 8 ~113 cm2.
Aire
d'une pizza carrée : 342 = 1156 cm2 ; aire d'une
part : 1156 / 9 ~128 cm2, part la plus grande.
|
Exercice 4.
Voici
les caractéristiques d’une piscine qui doit être rénovée :
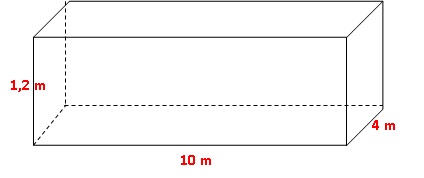
Débit de la pompe de vidange : 14 m3/h.
informations sur la peinture résine utilisée pour la rénovation
seau de 3 litres ; un litre recouvre une surface de 6 m2
; 2 couches nécessaires ; prix du seau : 69,99 €.
1. Le propriétaire
commence par vider la piscine avec la pompe de vidange.
Cette piscine est remplie à ras bord. Sera-t-elle vide en moins de 4
heures ?
Volume de la piscine : 1,2 x 10 x 4 = 48 m3.
Durée de la vidange : 48 / 14 =3,4 heures, valeur inférieure à 4 heures.
2. Il repeint
ensuite toute la surface intérieure de cette piscine avec de la
peinture résine. Quel est le coût de la rénovation ?
Aire du fond = 10 x4 = 40 m2.
Aire latérale : (10 +4 +10 +4 ) x1,2 =33,6 m2.
Aire totale : 73,6 m2.
Nombre de seau pour deux couches de peintures : 2 x 73,6 /18=8,17
, donc 9 seaux.
Coût : 9 x 69,99 = 629,91 €.
Exercice 5.
Agnês envisage de peindre la façade de son hangar.
Une seule couche de
peinture suffit.
Renseignements concernant un pot de peinture
Volume : 6 L ; temps de séchage : 8 h ; surface couverte : 24 m2
; prix : 103,45 €.
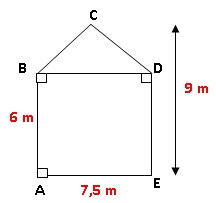
1. Quel est le
montant minimum à prévoir pour l’ achat des pots de peinture ?
Aire du rectangl : 6 x7,5 = 45 m2.
Aire du triangle de hauteur égale à 3 m : 7,5 x3 / 2 =11,25 m2.
Aire de la façade : 45 +11,25 = 56,25 m2.
Il faut prévoir 3 pots de peinture.
Coût : 3 x103,45 = 310,35 €.
2. Agnès achète la
peinture et tout le matériel dont elle a besoin pour ses travaux.
Le montant total de la facture est de 343,50 €.
Le magasin lui propose de régler 2 /5 de la facture aujourd’hui et le
reste en trois mensualités identiques.
Quel sera le montant de chaque mensualité ?
Montant des trois mensualités : 343,50 -343,5 x2 /5 = 343,50 x3 / 5 =
206,1 €
Montant d'une mensualité : 206,1 / 3 = 68,7 €.
|
Exercice 6.
Laurent
s’installe comme éleveur de chèvres pour produire du lait afin
de fabriquer des fromages.
PARTIE 1 : La production de lait
Chèvre de race alpine :
Production de lait : 1,8 litre
de lait par jour et par chèvre en
moyenne.
Pâturage : 12 chèvres maximum
par hectare.
Plan simplifié des surfaces de
pâturage.
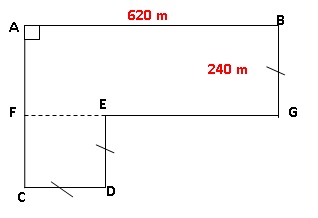
1. Prouver que
Laurent peut posséder au maximum 247 chèvres.
Aire du rectangle ABGF : 620
x240 =148 800 m2= 14,88 ha.
Aire du carré CDEF : 240 x240 =
57600 m2= 5 76 ha.
Aire totale : 14,88 + 5,76 =
20,64 ha.
Nombre maximal de chèvres :
20,64 x12 ~247 .
2. Dans ces
conditions, combien de litres de lait peut-il espérer produire par jour
en moyenne ?
247 x1,8 = 444,6 L.
Le stockage du lait
Laurent veut acheter une cuve
cylindrique pour stocker le lait de ses
chèvres.
Il a le choix entre 2 modèles :
• cuve A : contenance 585 litres
• cuve B : diamètre 100 cm,
hauteur 76 cm
Il choisit la cuve ayant la
plus grande contenance. Laquelle va-t-il
acheter ?
Volume de la cuve B : pr2h
= 3,14 x502x76 =596 903 cm3
= 596,9 L. Il chosit
la cuve B.
Exercice
7.
Marc veut fabriquer
un bonhomme de neige en bois.
Pour cela, il achète deux boules : une boule pour la tête de rayon 3 cm
et une autre boule pour le corps dont le rayon est 2 fois plus grand.
1. a. Vérifier que
le volume de la boule pour la tête est bien 36p cm3.
4 / 3 p r3
= 4 / 3 p x33=36p cm3.
b.
En déduire le volume exact en cm3 de la boule pour le corps.
23x36p = 288 p cm3.
2. Marc coupe les
deux boules afin de les assembler pour obtenir le bonhomme de neige.
Il coupe la boule représentant la tête par un plan situé à 2 cm de son
centre.
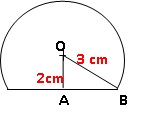
Quelle est l’aire de la surface d’assemblage de la tête et du corps ?
Arrondir le résultat au cm2.
AB2 = OB2 -OA2=9-4=5.
Aire du disque de rayon AB : p
AB2 = 3,14 x5 = 15,7 ~16 cm2.
|





