Géométrie,
fonction exponentielle, fonction logarithme et convexité, bac
Amérique du Nord 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
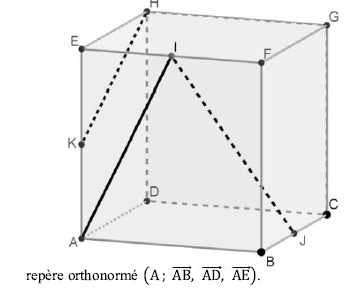
On considère le cube suivant. I est le
milieu du segment [EF] ; J est le milieu du segment (BC] ; K est le
milieu du segment [AE].
1. Les droites
(AI) et (KH) sont-elles parallèles ? Justifier.
A(0 ; 0 ; 0) ; I( 0,5 ; 0 ; 1).
Coordonnées d'un vercteur directeur de la droite (AI) : 0,5 ; 0 ; 1.
K( 0 ; 0 ; 0,5 ) ; H(0 ; 1 ; 1)
Coordonnées d'un vercteur directeur de la
droite (KH) : 0 ; 1 ; 0,5.
Les vecteurs directeurs de ces droites n'étant pas colinéaires, les
droites (AI) et (KH) ne sont pas parallèles.
2. a. Donner les coordonnées des
points I et J.
I( 0,5 ; 0 ;
1) ; J( 1 ; 0,5 ; 0).
b. Montrer que les
vecteurs suivants sont coplanaires.
E(0 ; 0 ; 1) ; C( 1 ; 1 ; 0).
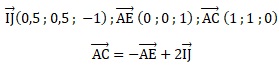
L'un des vecteurs est une combinaison linéaire des deux autres : ces
vecteurs sont donc coplaniares.
On considère le plan P d'équation x +3y -2z +2=0 ainsi que les droites d1
et d2 définies par leurs représentation paramétriques
respectives :
x = 3+t ; y = 8-2t ; z = -2+3t.
x = 4+t ; y = 1+t ; z = 8+2t ; t réel.
3. Ces droites
sont-elles parallèles ? Justifier.
Coordonnées d'un vecteur directeur de la droite d1 : 1 ; -2
; 3.
Coordonnées d'un vecteur directeur de la
droite d2 : 1 ; 1 ; 2.
Les vecteurs directeurs de ces droites n'étant pas colinéaires, les
droites ne sont pas parallèles.
4. Montrer que la droite d2
est parallèle au plan P.
Dans l'hypothèse où le plan P et la
droite d2 sont sécants, les coordonnées du point
d'intersection vérifient :
x +3y -2z +2=0 et x = 4+t ; y = 1+t ; z = 8+2t .
4+t +3(1+t) -2(8+2t) +2 = 0.
-11+0 t =0, c'est impossible.
L'hypothèse est rejetée ; le plan P et la droite d2 sont
parallèles.
5. Montrer que le
point L(4 ; 0 ; 3) est le projeté orthogonal du point M(5 ; 3 , 1) sur
le plan P.
Coordonnées d'un vecteur normal au plan P : (1 ; 3 ; -2).
Coordonnées du vecteur ML : (1 ; 3 ;-2).
Ces deux vecteurs sont donc colinéaires.
L appartient-il au plan P ?
Si L appartient au plan P :
xL +3yL -2zL +2=0.
4 +3*0-2*3+2=0 est vérifié.
Le point L(4 ; 0 ;
3) est donc le projeté orthogonal du point M(5 ; 3 , 1) sur le plan P.
Fonction exponentielle,
convexité.
Pour chacune des affirmations suivantes, indiquer si elle est juste ou
fausse. Justifier.
Affirmation
1. Pour tout réels a et b, (ea+eb)2
= e2a+e2b. Faux.
(ea+eb)
(ea+eb)
=ea .ea +ea .eb
+eb
.ea +eb .eb =ea+a +2ea+b
+eb+b .
Affirmation 2. Dans le plan muni d'un repère,
la tangente au point A d'abscisse 0 à la courbe représentative de la
fonction f définie sur R par f(x) =-2+(3-x)ex admet
pour équation réduite y = 2x+1. Vrai.
Calcul de f '(x) en posant u = 3-x et v = ex ; u' = -1 ; v'
= ex.
f '(x) = u'v+v'u =
-ex +(3-x)ex= (2-x)ex.
Coefficient directeur de la tangente à la courbe en x=0 : f '(0) = 2.
Le point de coordonnées (0 ; f(0) soit (0 ; 1) appartient à la tangente.
Equation de la tangente : y = 2x +b ; 1 =2*0+b ; y = 2x+1.
Affirmation
3. La limite en plus l'infini de e2x-ex+3/x
est égale à zéro. Faux.
e2x(1-1/ex+3/(xe2x)).
En plus l'infini : 1/exet
3/(xe2x) tendent vers zéro ; e2x
tend vers plus l'infini.
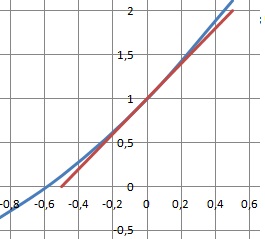
Affirmation
4. L'équation 1-x+e-x =0 admet une seule solution
appartenant à [0 ; 2]. Vrai.
Soit f(x) = 1-x+e-x
; f '(x) = -1-e-x.
f '(x) est négaitivesur [0
; 2] ; f (x) est strictement décroissante sur cet intervalle de f(0 )=2 à f(2) =-1+e-2
~-0,86.
D'après le théorème de la bijection, l'équation f(x) = 0 possède une seule solution sur [0 ; 2].
Affirmation
5. La fonction g définie sur R par g(x) = x2-5x+ex
est convexe. Vrai.
g'(x) = 2x-5+ex.
g"(x) =2+ex >0.
La dérivée seconde étant positive sur R, la fonction est convexe.
|
...
|
....
|
Fonction logarithme népérien et convexité.
On considère la courbe Cf
représentative d'une fonction f, deux fois dérivable sur ]0 ; +oo[.
Cette courbe admet une tangente horizontale T au point A(1 ; 4).
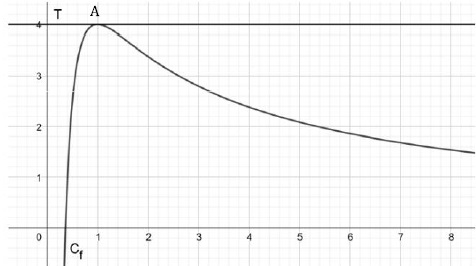
1. Préciser les valeurs de f(1) et f '(1).
f(1) = 4 ; f '(1) =0, tangente horizontale en A.
On admet que la fonction f est définie par f(x) = (a+b ln(x)) / x, a et b étant deux réels.
2. Montrer que f
'(x) = (b-a-b ln(x) ) / x2.
u = a +b ln(x) ; v = x ; u' = b /x ; v' = 1.
f '(x) =(u'v-v'u) / v2 =( b- a-bln(x)) / x2.
3. En déduire les valeurs de a et b.
f(1) =(a + bln(1)) /1 = a = 4.
f '(1) = ( b- a-bln(1)) / 12=b-a = 0 ; b = a = 4.
Par la suite on admet que f(x) = (4 +4 ln(x) ) / x.
4.
Déterminer les limites de f en zéro et en plus l'infini.
En zéro : 4 + ln(x) tend vers moins l'infini ; le dénomonateur tend vers 0+.
(4+ln(x)) / x tend vers moins l'infini.
En +oo : 4 /x tend vers zéro et par croissance comparée ln(x) / x tend vers zéro.
f(x) tend donc vers zéro.
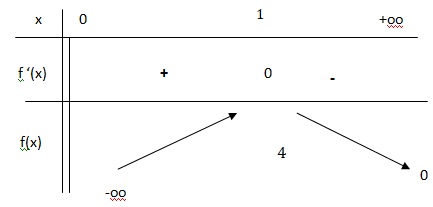
5. Déterminer le tableau de variation de f.
f
'(x) = (-4 ln(x) ) / x2.
Si x = 1, f '(x) = 0 ; f présente un extrémum.
Si x appartient à ]0 ; 1[, f '(x) >0 et f est strictement croissante.
Si x appartient à ]1 ; +oo[, f '(x) < 0 et f est strictement décroissante.
6. Montrer que f "(x) =(-4+8ln(x)) / x3.
f '(x) = (-4 ln(x) ) / x2.
On pose u = -4ln(x) et v = x2 ; u' = -4 /x ; v' = 2x.
(u'v-v'u) / v2 =(-4 x+8x ln(x)) / x4 =(-4+8ln(x)) / x3.
7. Montrer que la courbe possède un point unique d'inflexion dont on précisera les coordonnées.
f "(x) s'annule et change de signe pour -4+8ln(x) = 0 soit 2 ln(x) = 1 ; ln(x) = 0,5 ; x = e0,5~1,65.
f(e0,5)=4(1+ln(e0,5) )/ e0,5 =6 e-0,5 ~3,64.
.
|
|