Mathématiques,
probabilités, suites, bac Amérique du Nord 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Un laboratoire vient d'élaborer un nouveau test anti-dopage.
Partie A.
Une étude sur ce test donne les résultats suivants :
- si un athlète est dopé, la probabilité que le test soit positif est 0,98 ( sensibilité du test).
- si l'athlète n'est pas dopé, la probabilité que le résultat soit négatif est 0,995 ( spécificité du test).
On
fait subir le test à un athlète sélectionné au hasard au sein d'une
compétition. On note D l'événement " l'athlète est dopé" et T
l'événement " le test est positif". La probabilité de l'événement D est
égale à 0,08.
1. Traduire la situation à l'aide d'un arbre pondéré.
2. Démontrer que P(T) = 0,083.
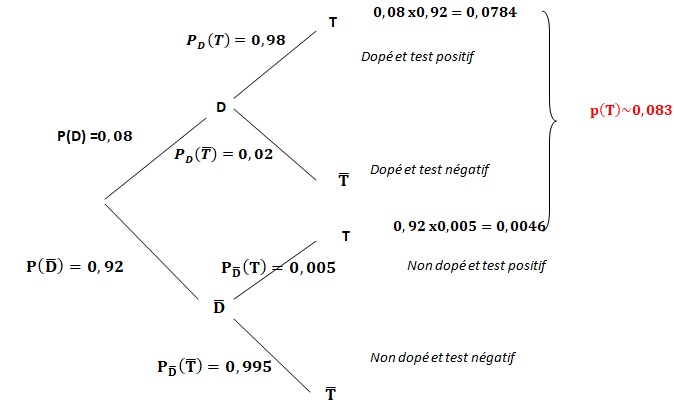
3.a. Sachant qu'un athlète présente un test positif, quelle est la probabilité qu'il soit dopé ?
PT(D)= P(T n D) / P(T) = 0,0784 / 0,083 =0,945.
b.
Le laboratoire décide de commercialiser le test si la probabilité de
l'événement " un athlète présentant un test positif est dopé " est
supérieure à 0,95. Ce test sera t-il commercialisé ? Justifier.
Non car PT(D)=0,945 < 0,95.
Partie B.
Dans une compétition, on admet que la probabilité qu'un athlète contrôlé présente un test positif est 0,103.
1.
Dans cette question, les organisateurs décident de contrôler 5 athlètes
au hasard. On note X la variable aléatoire égale au nombre d'athlètes
présentant un test positif parmi les 5 contrôlés.
a. Donner la loi suivie par X.
Loi binomiale de paramètre n = 5 et p = 0,103.
b. Calculer l'espérance de X et interpréter.
E(X) = np = 5 x0,103 =0,515.
En moyenne sur 10 athlètes contrôlés, un seul est dopé.
c. Quelle est la probabilité qu'au moins un des 5 athlètes contrôlés présente un test positif ?
1-P(X = 0) =1-0,580=0,42.
2. Combien
d'athlètes faut-il contrôler au minimum pour que la probabilité de
l'événement " au moins un athlète contrôlé présente un test positif"
soit supérieure ou égale à 0,75 ? Justifier.
Pour 13 athlètes contrôlés : 1-P(X =0) =1-0,243 =0,757.
Pour 12 athlètes contrôlés : 1-P(X =0) =1-0,271=0,729.
Il faut contrôler au minimum 13 athlètes.
|
...
|
....
|
2. Suites.
Un
biologiste s'intéresse à l'évolution de la population d'une espèce
animale sur un île. Au début de l'année 2020, cette population comptait
600 individus. L'espèce sera menacée d'extinction sur cette île si sa
population devient inférieure ou égale à 20 individus.
Cette population est modélisée par une suite (un) définie par : u0 = 0,6 ; un+1= 0,75un(1-0,15 un).
un : nombre d'individus en milliers ; en 2020, n = 0.
1. Estimer le nombre d'individus présents au début 2021 et au début 2022.
u1= 0,75 u0(1-0,15 u0) = 0,75 x0,6(1-0,15 x0,6) =0,4095~0,41.
u2= 0,75 u1(1-0,15 u1) = 0,75 x0,4095(1-0,15 x0,4095) ~0,288.
Soit f la fonction définie sur l'intervalle [0 ; 1] par f(x)=0,75x(1-0,15x.)
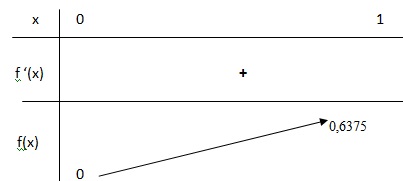
2. Montrer que f est croissante et dresser son tableau de variation.
On pose u = 0,75 x et v = 1-0,15x.
u' = 0,75 ; v' = -0,15 ; u'v+v'u = 0,75(1-0,15x) -0,15 x0,75 x =0,75 (0,85 -0,15x).
f '(x) =0 si x = 0,85 /0,15 =17 /3.
f '(x) >0 si x < 17 / 3.
La dérivée est positive sur [0 ; 1] et la fonction est strictement croissante sur cet intervalle.
3. Résoudre sur cet intervalle, f(x) =x.
0,75x(1-0,15x.) = x.
0,75x(1-0,15x.)- x= 0
x(0,75(1-0,15x)-1)=0
x(-0,25-0,1125x)=0
x = 0 est la seule solution sur [0 ; 1].
On remarquera que un+1 = f(un).
4.a Démontrer par récurrence que 0 < un+1 < un < 1.
Initialisation :0 < u1 < u0 < 1 est vraie.( u1 = 0,41 et u0 = 0,6).
Hérédité : la propriété est supposée vraie au rang n.
0 < un+1 < un < 1.
La fonction f étant strictement croissante : f(0) < f(un+1) < f(un )< f(1).
Soit 0 < un+2 < un+1 < 0,6375 < 1.
la propriété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang 1 et héréditaire, elle est vraie pour tout entier n.
b. En déduire que la suite (un) est convergente.
c. Déterminer la limite de cette suite.
f(0) < f(un+1) < f(un )< f(1).
0 < un+1 < un < 1.
La suite est décroissante et minorée, donc elle converge.
5. Le biologiste a l'intuition que l'espèce sera tôt ou tard menacée d'exctinction.
a. Justifier, que selon ce modèle, il a raison.
La suite (un) converge vers zéro. L'espèce sera tôt ou tard menacée d'exctinction.
b. Le biologiste a programmé en langage python la fonction menace() ci-dessous.
def menace()
u = 0,6
n=0
while u > 0,02
u = 0,75*u*(1-0,15*u)
n=n+1
return n
Donner la valeur numérique renvoyée et interpréter.
0,75x(1-0,15x) > 0,02 ;
-0,1125 x2+0,75x-0,02 > 0.
Solution(s) de : -0,1125 x2+0,75x-0,02 =0.
Discriminant D = 0,752-4*0,1125*0,02 =0,5535 =0,7442.
Solution retenue : (-0,75 -0,744) / (-2*0,1125) =6,64.
soit n = 6,64 / 0,6 ~11.
En 2031, la population sera en voie d'extinction.
.
|
|