Math�matiques, bac STI2Det STL Antilles 2020.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.

.. ..


.
.
.. ..
......


...
Exercice 1. QCM. Une seule des 4 r�ponses propos�es est exacte.
1. On donne le tableau de variation d'une fonction f d�finie et d�rivable sur R. On note C sa courbe repr�sentative et f ' sa d�riv�e.

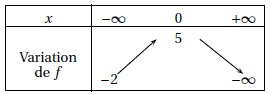
On a ;
a. f '(0) = 5. Faux. ( f (0) = 5).
b. Si x < 0 alors f '(x) < 0. Faux.
Si x < 0, f(x) est croissante et donc  f '(x) > 0.
c. La courbe C admet une asymptote parall�le � l'axe des abscisses. Vrai.
Quand x tend vers moins l'infini, alors f(x) tend vers -2.
d. La courbe C admet une asymptote parall�le � l'axe des ordonn�s. Faux.

2. Pour tout r�el strictement positif b le nombre ln(b-3) est �gal � :
a. -3b.
b. -3 ln(b). Vrai.
c. (ln(b))-3.
d.1 /(ln(b3).
 ln(b-3) = -3 ln(b).

3. Soit x un nombre r�el. On consid�re le nombre complexe z dont la partie r�elle est x et dont la partie imaginaire est 3. La partie imaginaire de z2 est �gale � : a. 6.  ; b. 9 ; c. 6x Vrai ; d. (6x)i.
z = x +3i ; z2 =(x+3i)2 = x2 +(3i)2 +6xi =x2 -9+6xi.

4. Le plan complexe est muni d'un rep�re orthonorm�. Les points A, B et C ont pour affixes respectives zA = exp(i 2p/3),
zB = exp(i 4p/3) et zC = 2 exp(i 2p/3). Le graphique correct est :

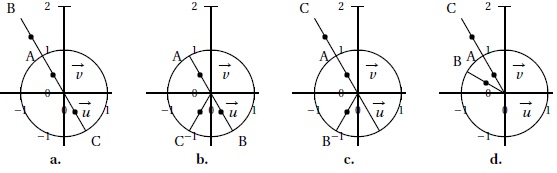
R�ponse c.

Exercice 2.
Une compagnie a�rienne annonce qu'elle souhaite am�liorer sa rentabilit�, tout en surveillant la fiabilit� de ses appareils et en garantissant la satisfaction de ses passagers.
Partie A. Rentabilit�.
1. La compagnie �tudie le taux de remplissage de ses avions. Ce taux est mod�lis� par la variable al�atoire R suivant la loi normale de moyenne � =0,85 et d'�cart type s = 0,05.
a. Donner P(R < 0,85).
P(R < 0,85) = 0,500.
b. D�terminer la probabilit� que le taux de remplissage d'un avion soit compris entre 0,8 et 0,9.
P(R < 0,8) = 0,158655 ; P(R < 0,9) = 0,841345 ;
 P(0,8 < R < 0,9) =0,841345 - 0,158655 ~0,683.
2. On consid�re que, pour un passager ayant achet� un billet, la probabilit� de se pr�senter � l'embarquement pour ce vol est 0,96. La compagnie d�cide de pratiquer la surr�servation. Pour cela elle vend 250 billets pour un vol dans un avion ne contenant que 246 places. Soit X la variable al�atoire comptant le nombre de passagers se pr�sentant � l'embarquement pour ce vol.
 X suit la loi binomiale de param�tre n = 250 et p = 0,96.
a. D�terminer l'esp�rance de la variable X et interpr�ter.
� = np = 250 x0,96 =240.
En moyenne, 240 personnes se pr�sentent � l'embarquement.
b. Donner la probabilit� qu'au moins 247 passagers se pr�sentent � l'embarquement.
P (X < 247) ~0,998.

Partie B. Fiabilit�.
A la suite d'une visite de maintenance, la compagnie d�cide de remplacer un composant �lectronique de la sonde de temp�rature par un nouveau composant plus fiable.
On admet que le temps de fonctionnement avant panne de ce nouveau composant, exprim�e en ann�es, est une variable al�atoire T qui suit la loi exponentielle de param�tre l = 0,025.
1. D�terminer le temps moyen de fonctionnement avant panne de ce nouveau composant.
� = 1 / l = 1 / 0,025 =40 ann�es.
2. Calculer P(T < 40).
P(T < 40) = 1 -exp(-0,025 *40) = 1-0,3679 ~0,632.
3. La prochaine visite de maintenance pour cet avion est pr�vue dans 2 ans. D�terminer la probabilit� que ce composant �lectronique ne subisse pas de panne avant le prochaine visite.
1-P(T < 2) = exp(-0,025 *2) = 0,951.

Partie C. Satisfaction des passagers.
La compagnie affirme que 90 % des passagers sont satisfaits. Une association de consommateurs proc�de � une enqu�te ind�pendante aupr�s de 450 passagers et constate que 63 clients sont m�contents. Au seuil de 95 %, peut-on mettre en doute l'affirmation de la compagnie ? Justifier.
n = 450 ; p = 0,90 ; [ p(1-p) / n ]�= (0,9 x0,1 / 450)� =0,0141.
1,96 x[ p(1-p) / n ]�=1,96 x0,0141 ~0,0278.
0,90 -0,0278 ~0,872 ; 0,90 +0,0278 ~0,928.
Intervalle de fluctuation asymptotique � 95 % : [0,872 ; 0,928 ].
Fr�quence observ�e :1- 63 / 450 = 0,86.
La fr�quence observ�e n'appartient pas � l'intervalle de fluctuation. On peut mettre en doute l'affirmation de la compagnie.

...
....

 Exercice 3.
En 2015, la consommation d'�lectricit� li�e aux usages du num�rique �tait de 56 TWh.
1. On admet que la consommation augmente de 4 % par an depuis 2015.
Pour tout entier n, on note un la consommation d'�lectricit� li�e au usages du num�rique en France, exprim�e en TWh, pour l'ann�e 2015 +n. Ainsi u0 = 56.
a. Calculer la consommation d'�lectricit� li�e aux usages du num�rique en 2016.
u1 = 56 x1,04 =58,24 TWh.
b. D�terminer la nature de cette suite et donner ses �l�ments caract�ristiques.
Suite g�om�trique de raison 1,04 et de premier terme 56.
c. Pour tout entier n, exprimer un en fonction de n.
un = 56 x1,04n.
d. On admet que chaque ann�e en France, la consommation d'�lectricit�, tous usages confondus, est �gale � 480 TWh.
Est-il exact d'affirmer qu'en 2030, plus de 20 % de la consommation d'�lectricit� sera li� au num�rique ? Justifier.
480 x0,20 = 96.
n = 15 ; u15 = 56 x1,0415 ~100,85, valeur sup�rieure � 96. C'est exact.
2. On estime qu'en 2030, en France, la consommation d'�lectricit� li�e aux usages du num�rique sera de 101 TWh.
A partir de 2030 on envisage une baisse de consommation �lectrique li�e aux usages du num�rique de 3 TWh par an.
D�terminer en quelle ann�e la consommation d'�lectricit� li�e au num�rique sera �gale � la consommation en 2015.
1-3 / 100 = 0,97.
Suite g�om�trique de raison 0,97 et de premier terme 101.
vn =101 x0,97n.
101 x0,97n =56 ; 0,97n = 56 / 101 = 0,5544.
n = ln(0,5544) / ln(0,97) ~19,36 (n = 20 ; ann�e 2030 +20 = 2050).

Partie B.
On consid�re un conducteur �lectrique repr�sent� par une tige m�tallique rectiligne fix�e en ces deux extr�mit�s.
Dans le rep�re orthonorm� ci-dessous, d'unit� graphique 1 cm, la tige m�talllique est mod�lis�e par le segment [OP], o� P d�signe le point de coordonn�e (1 ; 0).

Sous l'effet de la temp�rature, la tigese d�forme en se dilatant.  La tige d�form�e est sch�matis�e par la courbe C ci-dessous passant par les points O et P. La tangente � la courbe C au point O passe par le point T de coordonn�es (0,3 ; 0,3).

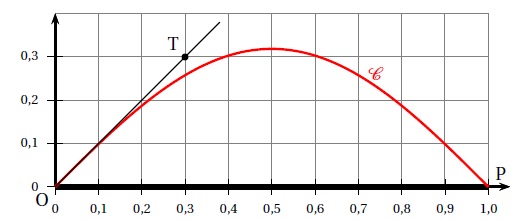
On admet que la courbe C est la courbe repr�sentative d'une fonction f, solution de l'�quation diff�rentielle (E) dans laquelle y est une fonction de la variable x, d�finie et deux fois d�rivable sur [0 ; 1 ].
(E) : y" +p2y = 0.
1. D�terminer les solutions de (E) sur [0 ; 1].
Equation caract�ristique : r2 +p2 = 0 ; r = � i p.
y = A cos (px) +B sin (px).
2.a. Sans justifier donner la valeur de f(0).
 f(0) = 0.
2.b. D�terminer la valeur de f '(0). Justifier.
Le coefficient directeur de la tangente en O est �gal � 0,3 / 0,3 = 1.
f '(0) = 1.
2.c. En d�duire que f(x) =1 / p sin (px).
y(0) = A=0 ; y = B sin (px).
y' = pB cos(px).
y'(0) = pB =1 ; B = 1 / p.
y = 1 / p sin (px).
3. On consid�re que la tige subit une d�formation irr�versible lorsque le maximum de la fonction f est sup�rieur � 1 /3. Est-ce le cas. Justifier.
f ' (x)= cos(px).
La d�riv�e s'annule pour x = 0,5.
f(0,5) = sin (0,5 p) / p = 1 / p ~0,318, valeur inf�rieure � 1 /3.
La d�formation n'est pas irr�versible.

Exercice 4.
On s'int�resse � l'�volution depuis 1958 de la concentration en dioxyde de carbone de l'atmosph�re. Cette concentration est exprim�e en partie par million en volume ( ppmv).
Partie A. Mod�lisation.
La concentration est mod�lis�e par une fonction d�finie sur [0 ; +oo[ par : f(t) = 280 + keat o� a et k sont deux constantes r�elles et t le temps �coul� depuis le 1er janvier 1958, exprim� en ann�e.
1.a Le 1er janvier 1958, la concentration en CO2 vaut 315 ppmv. D�terminer la valeur de k.
f(0) = 280 +k = 315 ; k = 35.
1.b. Le 1er janvier 2018, la concentration en CO2 vaut 411,25 ppmv. D�terminer la valeur exacte de a.
t =60..
f(60) = 280 +35 e60a = 411,25.
35 e60a =411,25 -280 =131,25.
 e60a =131,25 / 35 = 3,75.
60 a =ln(3,75) ; a = ln(3,75) / 60 ~0,022.
2. On admet que f(t) = 280 +35e0,022t.
La concentration en CO2 mesur�e le 1er janvier 1994 �tait de 357 ppmv. Ce mod�le est-il pertinent ?
t = 1994-1958=36.
f(36) =280 +35 e0,022 x 36 =357,27. Ce mod�le est pertinent.
.
Partie B. Etude de la fonction f(t) = 280 +35 e0,022t.
1. Donner la limite de cette fonction en plus l'infini.
Quand t tend vers plus l'infini, le terme en exponentiel tend vers plus l'infini ; f(t) tend vers + oo.
2. D�terminer la d�riv�e f '(t) et en d�duire le sens de variation de (f(t) sur [0 ; +oo[.
f '(t) =35 x0,022 e0,022t =0,77 e0,022t.
f '(t) est strictement positive et f(t) est strictement croissante sur [0 ; +oo[.
3.a D�terminer une primitive F de la fonction f.
F(t) = 280 t +35 / 0,022 e0,022t.
b. On pose 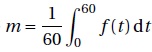 Exprimer m en fonction de F.
m =[ F(60) -F(0)] / 60 =280 +35 / (60 x0,022) e0,022x60 -35 /(0,022x60).
 m =280+26,515 e1,32-26,515 ~352,74.
Durant les ann�es 1958 �2018, la concentration moyenne de CO2 dans l'atmosph�re est 352,74 ppmv.

Partie C. Variabilit� saisonni�re.
La concentration de CO2 dans l'atmosph�re, exprim�e en ppmv, est alors mod�lis�e par la fonction g d�finie sur [0 ; +oo[ par :
g(t) = 280 + 35e0,022t+3,5 sin ( 2pt).
 t repr�sente le temps ( en ann�es) �coul� depuis le 1er janvier 1958.
1. Compl�ter l'algorithme ci-dessous afin que la variable C affiche successivement les concentrations en CO2 le 1er de chaque mois de l'ann�e 2018.
T = 60
Pour i allant de 0 � 12
C= 280 + 35*e0,022 * T+3,5 *sin ( 2 * p * T)
T = T + 1 /12
Afficher C
Fin Pour
2. Au d�but de quel mois de l'ann�e 2018 la concentration de CO2 est-elle minimale ?

.


  

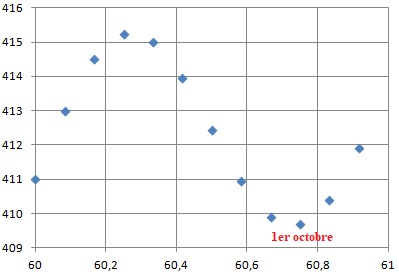
menu