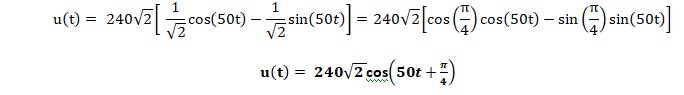Mathématiques, Bac Sti2d 2021.

Question 1.
On considère la fonction f définie sur ]0 ; +oo[ par f(x) = ax+b-ln(x) où a et b sont des réels. On note C la courbe représentative de f. On note A le point d'abscisse 0,5 appartenant à C. On trace T la tangente à C en A. La droite T est parallèle à l'axe des abscisses. Le point B(1 ; 1) appartient à C.

a. Donner la valeur de f(1). En déduire une relation entre a et b.
f(1) est l'ordonnée du point B ; f(1) = 1
1 = a+b-ln(1) ; 1 = a+b.
b. Justifier que f '(0,5) = 0. En déduire la valeur de a.
T tangente à la courbe C en A est parallèle à l'axe des abscisses ; le coefficient directeur de T est donc nul.
f '(0,5) = 0 ; f '(x) = a -1 /x ; f '(0,5) = a-1 /0,5 = a-2 =0 ; a = 2
c. En déduire la valeur de b.
a+b = 1 avec a = 2 ; b = -1.

Question 2.
Une entreprise achète une machine d'une valeur de 300 000 €. Cette machine perd de sa valeur au cours des années. Cette perte exprimée en euros, à l'instant t exprimé en année, est modéliisée par lea fonction f définie sur [0 ; 15] par f(t) = 300 000 (1-e^-0,09t).
Au bout de combien d'années la machine aura t-elle perdu la moitié de sa valeur ?
150 000 = 300 000 (1-e^-0,09t).
0,5 = 1-e^-0,09t ; 0,5 = e^-0,09t ; ln 0,5 = -0,09t ; ln2 =0,09 t ; t = ln 2 / 0,09 ~7,7. On retient t = 8 ans.

Question 3.
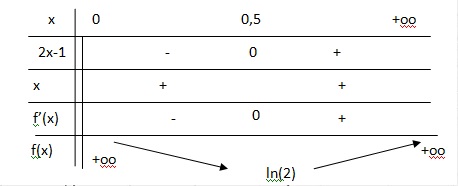
On considère la fonction f définie sur ]0 ; +oo[ par f(x) = 2x-1-ln(x)
a. Montrer que f '(x) = (2x-1) / x.
f '(x) = 2 -1 /x = 2x / x -1 /x = (2x-1) / x.
b. Dresser le tableau de variation de f(x).

Question 4.
On considère l'équation différentielle (E) : y'+0,0434y=0.
a. Déterminer sur ]0 ; +oo[ la solution P de cette équation qui vérifie y(0) = 6,75.
y = A e^-0,0434x avec A une constante.
y(0) =A e⁰ = 6,75.
P = 6,75 e^-0,0434x .
b. Un signal de puissance initiale P(0) = 6,75 mW parcourt une fibre optique. La puissance du signal, exprimée en mW, lorsque celui-ci a parcouru une distance de x km depuis l'entrée de la fibre est donnée par P(x), où P est la fonction définie à la question a.
Montrer que la perte de puissance une fois que le signal a parcouru 1 km depuis l'entrée est d'environ 287 µW.
P(1) =6,75 e^-0,0434 ~6,463 mW.
Perte : 6,75 -6,463 =0,287 mW = 287 µW.

Question 5.
Soit f la fonction définie sur R par f(x) = (x²+5x+4)e^x.
Soit F la fonction définie sur R par F(x) =(x²+3x+1)e^x.
a. Montrer que F'(x) =f(x).
On pose u = x²+3x+1 et v = e^x ; u' = 2x+3 ; v' = e^x.
u'v +v'u = (2x+3)e^x +(x²+3x+1)e^x = (x²+3x+4)e^x = f(x).
b. Calculer l'intégrale suivante :

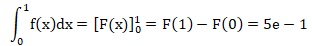
Question 6.
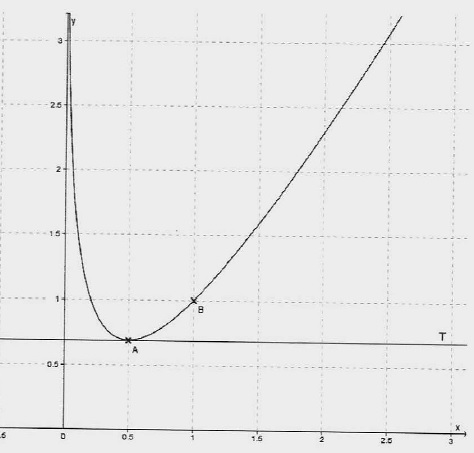
La tension aux bornes d'un générateur est donnée par u(t) = 240 cos(50t)-240 sin(50t).
U est exprimée en volt et le temps en seconde.
a. Démontrer l'expression suivante pour t >0.

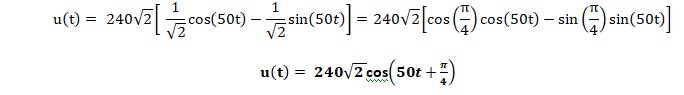
b. En déduire la fréquence f = w /(2p) exprimée en Hz.
w = 50 rad /s ; f = 50 / 6,28 ~7,96 ~ 8 Hz.