Mathématiques
appliquées,
bac STI2D
2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
Question
1.
a.
On considère l'équation différentielle (E) : y' +100y = 8.
Déterminer la solution v définie sur [0 ; +oo[ de cette équation qui
vérifie v(0) = 0.
Solution générale de y' +100 y=0 : y = A exp(-100t), avec A une
constante.
Solution particulière de (E) : y = 8 /100 = 0,08.
Solution générale de (E) : y = A exp(-100t) +0,08.
y(t=0) = A+0,08 = 0 ; A = -0,08.
v(t) = 0,08 (1-exp(-100t)).
b. Cette fonction v
modélise la vitesse ( m/s) de chute d'une bille dans un liquide
visqueux en fonction du temps écoulé depuis le début de la chute (
exprimé en seconde). Déterminer la vitesse, arrondie à 0,001 m /s, de
la bille à la date t = 0,01 s.
v(0,01) = 0,08 (1-exp(-1)) ~0,051 m /s.
Question 2.
La tension u, exprimée en volt, aux bornes d'un dipole en
fonction du temps t ( exprimé en seconde) est donnée par :
u(t) = 7*3½ /4 cos ( 100t) -7 / 4 sin(100 t).
a. Transformer
l'écriture de u sous la forme u(t) = Umax cos ( wt+f) où :
Umax représente la tenion maximale.
w
représente la pulsation en rad /s.
f représente
le déphasage exprimé en radian.
u(t)
= 7 /2 [ 3½ / 2 cos ( 100t) - 0,5 sin(100 t)].
u(t) = 7 /2 [ cos (p / 6) cos ( 100t) -sin (p / 6) sin(100 t)].
cos(a+b)
= cos (a) cos(b) -sin(a) sin(b).
u(t) =7 / 2 cos(100t +p/6).
Question 3.
On considère les deux
fonctions f et g définies et continues sur [0 ; 9] respectivement par :
f(x) = x2-2x+4 ; g(x) = 7x+4.
Déterminer la valeur exacte de l'aire, exprimée en unité d'aire, située
entre les courbes représentative de ces fonctions.
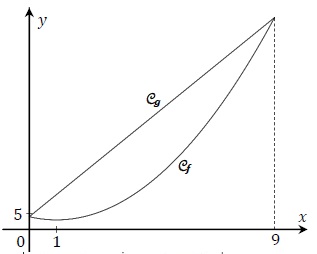
Aire située entre
la courbe Cg et 'xe des abscisses :
Primitive de g(x) : G(x) = 3,5 x2 +4x+ Cste.
G(9)-G(0) =3,5 *92 +4*9 +Cste -Cste = 319,5 unités d'aire.
Aire située entre la courbe
Cf et l'axe des abscisses :
Primitive de f(x) : F(x) =x3 /3 -x2+4x+Cste.
F(9)-F(0)=93 /3 -92+4*9+Cste -Cste =198
unités d'aire.
Aire du domaine situé entre les courbes :
319,5 -198 =121,5 unités d'aire.
Question 4.
La tension en volt aux bornes d'un condensateur lors de sa charge est
modélisée par : u(t) = E(1-exp(-t /(RC)).
E = 4 V ; R = 103 ohms ; C = 2 10-3 F.
Déterminer le temps de charge ( à 0,1 s près) nécessaire pour obtenir
une tension u(t) égale à la moitié de sa tension maximale.
RC =103
*2
10-3 = 2 s ; tension maximale u(t) = E.
0,5 E = E(1-exp(-0,5 t).
0,5 = 1-exp(-0,5t) ; exp(-0,5t)
= 0,5 ; -0,5 t = ln(0,5) ; t ~1,4 s.
|
|
Exercice 4
( 6 points)
Un joueur de minigolf se
trouve au sommet A d'une butte. Il vise le point C.
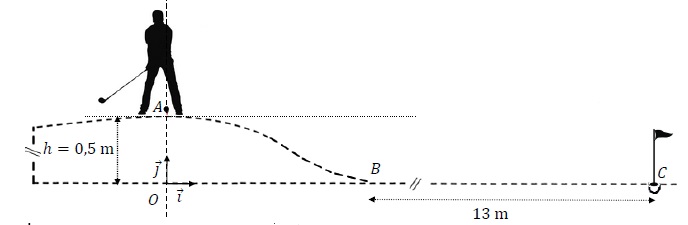
Le joueur frappe doucement la balle. La balle ne quitte pas le sol,
passe en B et se dirige vers C.
Masse de la balle m = 4,6 10-2 kg ; vitesse initiale en A :
1,50 m /s.
1. Quel est le
référentiel d'étude du mouvement de la balle ?
Le référentiel terrestre.
2. On étudie le
système {balle} du point A vers la base de la butte B. Les frottements
sont négligeables.
Au cours de cette phase, la variation de l'énergie cinétique du système
est égale au travail des forces extérieures appliquées au système.
a. Exprimer le
travail du poids entre A et B.
Travail moteur du poids en descente : W = mg OA = mgh.
b. Sans calcul
indiquer la valeur du travail de la réaction du support.
En absence de frottement, la réaction du support est perpendiculaire au
support. Une force perpendiculaire au support, ne travaille pas.
c. Exprimer la
variation d'énergie cinétique entre A et B.
Entre A et B, la variation d'énergie cinétique est égale au travail du
poids.
DEc
= mgh.
d. Vérifier que la
vitesse de la balle en B est 3,50 m /s.
½mv2B-½mv2A = mgh.
v2B-v2A
=2gh ; v2B=v2A
+2gh = 1,52 +2*10*0,5 =12,25 ; vB = 3,50 m /s.
3. On étudie le
système entre B et C. On prend t = 0 comme l'instant où la balle quitte
le point B.
Les frottements sont négligeables.
a. A quelles forces
est soumis le système ?
Le système est soumis à son poids, verticale vers le bas, et à l'action
du plan, perpendiculaire au support, vers le haut.
b. Justifier que la
vitesse entre B et C est v1 = 3,5 m /s.
Le poids et l'action du plan, perpendiculaires au plan, ne travaillent
pas et en conséquence ne modifient pas l'énergie cinétique du système.
4. On considère que
le système est soumis à une force de frottement 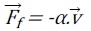
a. Appliquer le
principe fondamental de la dynamique sur le système et en déduire
l'équation différentielle que vérifie v en fonction de m et a.
En projection sur l'axe horizontal, -avx
= m a = m dvx/dt.
dvx / dt +a
/ mvx
=0.
b. On admet que la
fonction vx(t)
= K exp(-at / m)
est solution de cette équation différentielle.
A partir des conditions initiales, déterminer la valeur de K.
vx(0)
= 3,50 = K exp(0) = K.
c. La balle est en
C au temps t = 3,9 s.
La vitesse moyenne de la fonction vx
sur l'intervalle [0 ; 3,9) est donnée par :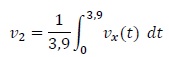
Sachant que a =
1,1 10-3 N m-1 s, montrer que v2 =
3,34 m /s.
a / m = 1,1 10-3
/ (4,6 10-2) ~0,0239.
Primitive
de exp(-0,0239 t) : -
exp(-0,0239 t) / 0,0239.
v2 =3,50 [ -exp(-0,0239 *3,9) -(-exp(0)] / (0,0239 * 3,9)
=3,50 [-0,911 +1] / 0,09321 ~3,34 m /s.
d. En comparant v1
et v2, quelle hypothèse peut-on en tirer sur l'impact des
frottements sur le mouvement ?
Ecart relatif : (3,50-3,34) / 3,50 =0,046 ( 4,6 %).
Les frottements peuvent être négligés entre B et C.
e. La balle
poursuit son mouvement au delà de C. Déterminer la limite de vx
en plus l'infini et interpréter le résultat.
exp(-at / m) tend vers zéro quand
t tend vers plus l'infini.
vx tend vers zéro quand le temps devient très grand.
La balle va finir par s'arrèter sous l'effet des frottements..
|
|