Mathématiques, bac STL
2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
...
|
|
Traiter 4 questions parmi les 6 proposées.
Les questions 1, 2 et 3 reposent sur la figure suivante.
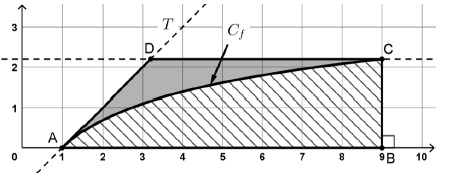
L'unité de longueur est le centimètre. La courbe Cf est celle de la fonction f définie sur [1 ; 9 ] par ln(x).
La droite T est la tangente à la courbe Cf au point A d'abscisse 1. B a pour coordonnées (9 ; 0).
La parallèle à l'axe des abscisses passant par C coupe la droite T en D.
On note D le domaine hachuré et A2 son aire exprimée en cm2.
Question 1.
1.a. Justifier que la tangente T a pour équation réduite y = x-1.
Coefficient directeur de T : f '(1) = 1 / 1 = 1.
T passe par le point de coordonnées (1 ; ln(1) =0).
y = x+b ; 0 = 1 +b ; b = -1. Par suite y = x-1.
On admet que D a pour coordonnées ( 2 ln(3) +1 ; 2 ln(3).
1.b Démontrer que l'aire du trapèze ABCD, notée A1 vaut 16 ln(3) -2(ln(3))2.
A1 = (AB +CD) x BC / 2.
AB = 8 ; CD =8-2 ln(3) ; BC = 2 ln(3).
A1 = [8+8-2ln(3)] x 2 ln(3) / 2 = 16 ln(3)-2(ln(3))2.
Question 2. Dans le but d'utiliser la méthode des rectangles pour estimer A2, on a écrit la fonction Python suivante :
from math import log as ln
def meth_rect(pas) :
s=0
x=1
while x < 9 :
s = s+ln(x)*pas
x=x+pas
return s
2.a. Laquelle des figures ci-dessous correspond à l'exécution de l'instruction meth_rect(2) ?
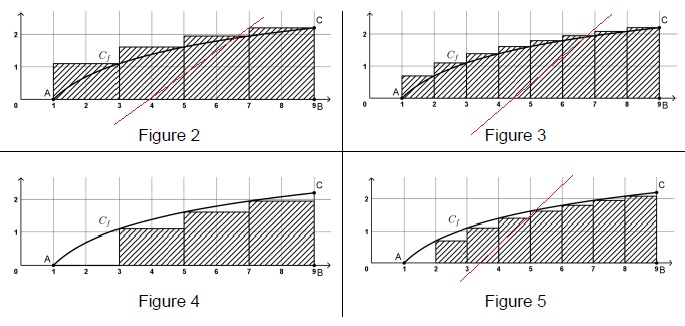
x=1 ; s = 0 +ln(1)*2 = 0 ; x=1+2=3.
x=3 ; s = 0+ln(3) *2 ; x = 3+2 = 5.
x=5 ; s = 2 ln(3)+ln(5) *2 ; x = 5+2 = 7.
x = 7 ; s = 2 ln(3) +2ln(5)+2 ln(7) ; x = 7+2 =9.
2.b. Comparer A2 à la valeur 9,307920700315046 renvoyée par l'exécution de meth_rect(2).
L'aire A2 est supérieure à la valeur renvoyée par ce programme.
Question 3.
3.a Démontrer que la fonction F définie sur [1 ; 9 ] par F(x) =xln(x)-x est une primitive de f.
On dérive F en posant u = x et v = ln(x) ; u' =1 et v' = 1 /x.
u'v+v'u = ln(x) +x / x = ln(x)+1.
F '(x) = ln(x) +1 -1 = ln(x).
3.b En déduire la valeur exacte de A2.
A2 = F(9) - F(1) = 9 ln(9)-9 -(ln(1)-1) = 9 ln(9)-8 ~11,775 cm2.
Question 4.
On considère la fonction f définie sur R par f(x) =(3x+2)e-x.
4.a Montrer que f '(x) = (-3x+1)e-x.
On pose u = 3x+2 et v = e-x ; u' = 3 ; v' = -e-x.
u'v+v'u = 3e-x-(3x+2)e-x=e-x(-3x+1)
4.b. Etudier le sens de variation de f sur R.
e-x est toujours positif ; le signe de la dérivée est celui de -3x+1.
-3x+1 = 0 ; x = 1 /3.
Si x < 1/3 : f '(x) > 0 et f(x) est strictement croissante.
Si x > 1 /3 : f '(x) < 0 et f(x) est strictement décroissante.
Si x = 1 /3, f(x) présente un maximum.
|
Question 5.
Le triangle PQR a les propriétés suivantes :
Déterminer la longueur PR.
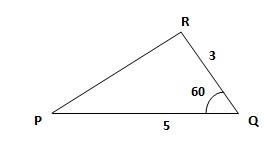
PR2 = PQ2 +QR2 -2 PQ . QR cos 60 =25 + 9-30 cos 60 =34-15 = 19 ; PR = 19½.
Question 6.
Soit f un réel appartenant à l'intervalle [0 ; p[ et f la fonction f(t) = cos ( 3t+f).
6.a. Montrer que pour tout réel t, f "(t) +9 f(t) = 0.
f '(t) = -3 sin ( 3t+f).
f "(t) = -9cos ( 3t+f).
f "(t) + 9 f(t) = -9cos ( 3t+f) + 9cos ( 3t+f) = 0.
6.b Déterminer la valeur de f telle que f(0) = 1 /2½.
1 /2½ = cos f ; f = p / 4.
|
|