Séparation d'acides aminés, des matériaux
pour se protéger du soleil, bac STL
2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
Séparation
d'un mélange d'acides aminés par électrophorèse.
Sous l'action d'un champ
électrostatique E supposé uniforme, de valeur E = 4,3 104 V m-1,
les acides aminés migrent vers la cathode.
Dans le repère du laboratoire supposé galiléen, on modélise une
molécule d'acide aminé ( la glycine +NH3-CH2-COOH)
par un point M, de charge positive q = 1,6 10-19
C, de masse m et on étudie son mouvement dans le capillaire. On
considère que les seules forces qui influent sur son mouvement sont la
force électrostatique F et la force de frottement 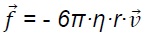 avec avec
h :
viscosité du fluide dans lequel se déplace l'espèce chimique en Pa s ;
r : rayon moyen de l'espèce chimique en mètre ;
v : la vitesse de l'espèce chimique en m / s.
Dans le cas de la glycine le facteur h r de la glycine est 1,1 10-13
N s m-1.
1. Citer la
relation littérale entre la force électrostatique s'exerçant sur
l'espèce chimique et le vecteur champ électrique E.
Le vecteur force électrique est proportionnel au vecteur champ
électrique. La constante de proportionnalité est la charge de l'espèce
chimique.
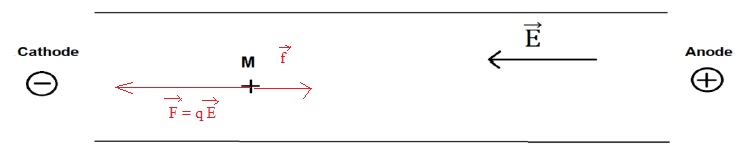
2.
Représenter sans soucis d'échelle, les forces qui s'exercent sur la
glycine, en sachant que la vitesse initiale est nulle. Justifier le
sens des forces.
La charge q étant positive, la force électrostatique F et le champ
électrique ont le même sens.
La force de frottement f a le sens contraire du déplacement.
3.
En utilisant la deuxième loi de newton, établir l'expression littérale
du vecteur accélération de l'espèce chimique.
En projection sur un axe horizontal orienté vers la gauche, cette loi
s'écrit :
qE -f = ma ; qE-6p
h r v
= m dv/dt.
4. A partir du résultat précédent,
on montre que la vitesse obéit à l'équation différentielle : dv /dt =
55 106 -17 109 v. (1).
a. Déterminer la solution générale
de (1).
Solution particulière de dv
/dt +17 109 v = 0 : v = k exp(-17 109 t) avec k
une contnte réelle.
Solution particulière de (1) : v = 55 106 / (17 109)
=3,235 10-3 m /s.
Solution générale de (1) : v
= k exp(-17 109 t) +3,235 10-3.
b. Sachant que v(0) = 0, montrer que
v(t) =3,2 10-3(1-exp(-17 109 t)).
k e0 +3,2 10-3 = 0 soit k = -3,2 10-3 ; v(t) = -3,2 10-3
exp(-17 109 t) +3,2 10-3.
c. Calculer la
limite de v(t) en +oo.
Le terme en exponentielle tend vers zéro et la vitesse tend vers 3,2 10-3
m /s.
d. Déterminer
l'instant t0 où la vitesse atteint 63 % de la vitesse
limite. Commenter en la comparant à la durée de l'expérience ( 15 min).
0,63 x3,2 10-3
=3,2 10-3(1-exp(-17
109 t0)).
0,63 = 1-exp(-17
109 t0) ; exp(-17 109
t0) =0,37 ; ln(0,37) =-17
109 t0 ; t0 ~5,8 10-11 s.
t0 est négligeable devant la durée de l'expérience. La
vitesse limite est très rapidement atteinte et le mouvement de l'espèce
chimique peut être considéré comme rectiligne uniforme.
5.
Montrer que la vitesse limite de la vitesse est v = qE /(6p hr).
En
régime permanent, la somme vectorielle des forces est nulle ; d'après
la première loi de Newton, le mouvement est rectiligne uniforme.
dvlimite /dt =0 ; qE-6p h r vlimite = qE
/(6p hr).
6. Calculer la durée nécessaire pour
la migration de la glycine, au sein du capillaire, sur une distance de
70 cm. Conclure en la comparant à la durée de l'expérience ( 15 min).
0,70 = 3,2 10-3 t ; t = 0,70 / (3,2 10-3) ~219 s
ou 3 min 39s, très inférieure à la durée de l'expérience.
|
Des matériaux pour se protéger du soleil.
Le photochromisme.
c'est la propriété de certains composés de changer de couleur sous
l'actions de radiations, puis à revenir à leur état initial
lorsque le rayonnement cesse.
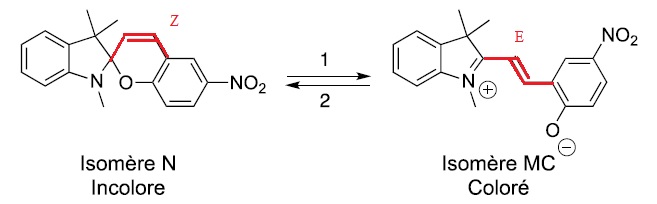
On se propose d'étudier un composé photochrome de formule brute C19H18N2O3
connu sous le nom 6-NO2-BIPS.
Il possède deux isomères, un isomère N incolore et un isomère coloré
appelé mérocyanine MC. Le passage de N à MC s'effectue par irradiation
dans l'UV. Au cours de cette réaction, une liaison carbone-oxygène est
rompue et la configuration d'une double liaison C+C est modifiée. La
forme MC revient spontanément à la forme N à températrure ambiante.
1. Déterminer la
configuration de cette liaison carbone-carbone.
On s'intéresse à la cinétique de la réaction de retour de la forme MC à
la forme N, modélisée par le sens 2 de l'équation précédente. On
utilise une méthode spectroscopique et on effectue le suivi cinétique à
la longueur d'onde l =
555 nm.
2. Justifier le
choix de cette longueur d'onde.
Seule la forme MC présente un maximum d'absorption à 555 nm.
3. Les isomères N
et MC sont polaires. Déterminer lequel de l'acétonitrile ou de l'éther
diéthylique est le solvant le plus judicieux pour effectuer le suivi
cinétique.
L'acétonitrile, plus polaire que l'éther diéthylique, est le plus
judicieux.

4. A partir des
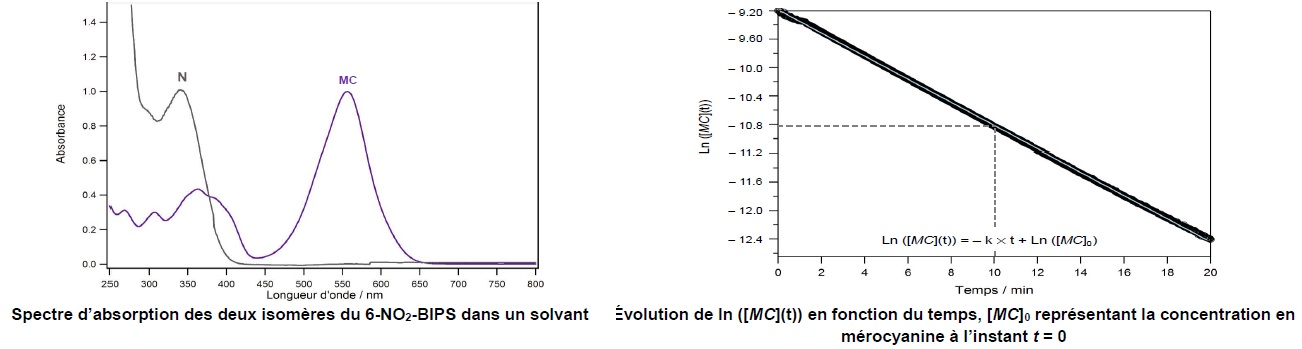
résultats expérimentaux, déduire l'ordre de la réaction.
La courbe d'équation ln([MC](t)) en fonction du temps est une droite,
donc réaction d'ordre 1.
5. Donner
l'expression de la vitesse de réaction en fonction de la concentration
en mérocyanine.
d[MC(t)] /dt = -k [MC(t)].
6. Etablir
l'équation de la loi d'évolution de la concentrtion [MC] en fonction du
temps et de la concentration initiale [MC]0.
d[MC] / [MC] = -kdt ; ln([MC]) = -kt + constante.
A t = 0 : ln([MC]0) = constante ;
ln([MC]) = -kt +
ln([MC]0) ; ln ([MC] / [MC]0)=
-kt.
7. A partir des
données expérimentales, déterminer la constante de vitesse k et le
temps de demi-réaction.
k = valeur absolue de la pente de la droite = 10,8 / 10 = 1,08 min-1.
A t½ : ln ([MC]t½
/ [MC]0)=ln(0,5) = -kt½ ; t½ = ln(2) /
k = ln(2) / 1,08 =0,64 min.
Les verres photochromiques actuels mettent environ 1 minute pour
s'assombrir complètement et 3 minutes pour s'éclaircir à nouveau.
8. Indiquer si le
6-NO2-BIPS pourrait être un matériau utilisable dans la
fabrication de ces verres de lunettes. Justifier.
3 minutes ~5 t½.
Le 6-NO2-BIPS peut être un matériau utilisable dans la
fabrication de ces verres de lunettes.
L'électrochromisme.
C'est la propriété de certaines substances chimiques de changer de
couleur de manière réversible. Ce phénomène peut être interprété à
l'aide de l'oxydo-réduction.
9. Le dihydrogène
forme avec les ions H+ un couple oxydant / réducteur. Ecrire
la demi-équation électronique associée.
2 H+ aq+ 2e- = H2
(g).
H2 (g).
La transformation du trioxyde de tungstène
WO3(s) en W4O11(s) peut être modélisée
par :
4WO3(s) +2
H+ aq+ 2e- =
W4O11(s) +H2O(l).
10. Ecrire
l'équation d'oxydo-réduction modélisant la réaction.
4WO3(s) +2
H+ aq+ 2e- =
W4O11(s) +H2O(l).
H2 (g) =2
H+ aq+ 2e- .
Ajouter et simplifier : 4WO3(s) +H2
(g) =
W4O11(s) +H2O(l) .
11. Indiquer si WO3(s)
est oxydé ou réduit.
WO3(s) gagne des électrons,
c'est un oxydant qui se réduit.
WO3(s) peut être extrait de CaWO4
par dissolution dans une solution d'acide chlorhydrique concentrée.
CaWO4 (s) +2H3O+aq
-->Ca2+aq +H2WO4(s) +2H2O(l).
On dispose de deux solutions d'acide chlorhydrique
( une solution à pH =1 et une solution à 6 mol / L).
12.
Indiquer la solution d'acide chlorhydrique à utiliser pour transformer
1,0 kg de CaWO4 (s) en calculant le
volume nécessaire de solution.
M(CaWO4)
= 288 g / mol).
n(CaWO4)
= 1,0 / 0,288 =3,47 mol.
n(H3O+aq)
= 2 x3,47 =6,94 mol.
Volume de solution concentrée ( 6 mol / L) : 6,94 / 6 ~1,2 L.
Volume de solution diluée( 0,1 mol / L) : 6,94 / 0,1 ~69 L.
On utilise la solution concentrée en portant une blouse, des gants et
des lunettes de protection.
|
|
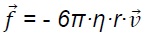 avec
avec


