Etude
thermique du four, panneaux solaires, accumulateur Ni-MH , bac STI2D
2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
Etude
thermique du four.
Caractéristiques du four : parallélépipede
; température intérieure 850 °C ; température de la piède 20°C.
Les parois du four sont constituées de 3 couches d'épaisseurs et de
matériaux différents, de l'intérieur vers l'extérieur :.
Réfractaires lourds : l
= 1,25 W m-1 C-1 ; e = 75 mm ; S = 0,371 m2.
Fibreux : l
= 0,20 W m-1 C-1 ; e = 20 mm ; S = 0,654 m2.
Isolants réfractaires : l = 0,13 W m-1 C-1
; e = 10 mm ; S = 0,710 m2.
Source : https ://www.borelswiss.fr/
1. Par analyse
dimensionnelle, déterminer l'unité de la résistance thermique.
Rth = e /(lS)
;
e /S s'exprime en m-1 ; 1 / l s'exprime en m C W-1
; Rth s'exprime en C
W-1 .
2. Déterminer la
résistance thermique de chaque couche.
R1 =0,075 /(1,25 x0,371) =0,1617 ~0,16 C W-1
.
R2 =0,020 /(0,20 x0,654) =0,153
~0,15 C
W-1 .
R3
=0,010 /(0,13 x0,710) =0,108 ~0,11 C W-1 .
3. En déduire la
résistance thermique de la paroi.
Rth = R1 +R2 +R3 =0,1617
+0,153 +0,108 =0,423 ~0,42 C W-1 .
4. Calculer la
valeur du flux thermique traversant la paroi.
F = DT / Rth =(850
-20) / 0,423 =1962 W ~2,0 kW.
5. Le four est
capable de fournir par effet Joule une puissance thermique Pth
= 6000 W pendant la montée en température, commenter la valeur du flux
thermique perdu à travers les parois durant cette phase.
Quand le four est chaud, la puissance perdue à travers les parois est
égale à Pth / 3.
Lors de cette phase, la puissance perdue à travers les parois augmente
de zéro à Pth / 3.
Etude d'un panneau solaire.
L'énergie produite pour alimenter ce four est fournie par des panneaux
photovoltaïques.
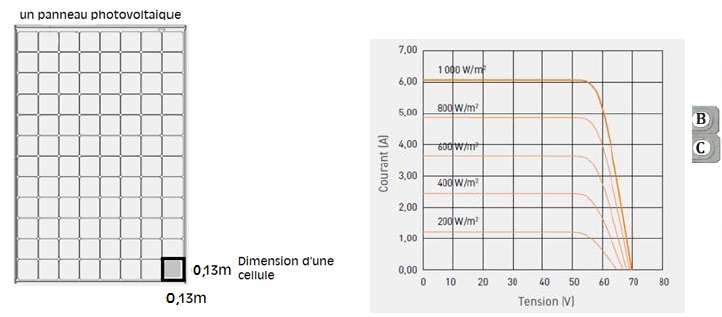
1. Calculer la
surface S d'un panneau photovoltaïque.
Surface d'une cellule : 0,13 x0,13 =0,0169 m2.
Nombre de cellules : 8 x12 = 96.
S =0,0169 x 96 =1,6224 ~1,6 m2.
2. En déduire la
puissance lumineuse PL reçue par un panneau sous une
irradiance de 1000 W m-2.
PL = 1,6224 x1000 =1622,4 W
~1,6 kW.
3. Montrer que la
puissance électrique maximale PEmax que peut délivrer un
panneau est 330 W.
Imax = 6,0 A ; Umax = 55 V ; PEmax =
6,0 x 55 = 330 W.
4. Calculer le
rendement de la cellule et identifier la technologie de ce pannrau.
Rendement = PEmax / PL = 330 / 1622,4 ~0,20 ( 20
%).
Capteur photovoltaïque monocristallin.
Faisabilité de
l'installation.
L'atelier, isolé du
réseau électrique, doit être alimenté de manière autonome par des
panneaux photovoltaïques.
1. Une toiture de 6
m par 4,5 m serait-elle adaptée pour y installer ces panneaux ?
Dimensions d'un panneau : 8 x0,13 =1,04 m ; 12 x 0,13 = 1,56 m.
On peut installer : 6 /1,56 ~3,84 ; 4,5 / 1,04 ~4,32.
3 rangées de 4 panneaux soit 12 panneaux.
Puissance électrique maximale disponible :12 x0,33 =3,96 ~4,0 kW.
Le four nécessite une puissance électrique de 6,0 kW.
La toiture est insuffisante.
2. Citer au moins un paramètre
n'ayant pas été pris en compte pouvant influer sur la quantité
d'énergie solaire reçue.
Irradiance moyenne pour la région ;
orientation et inclinaison de la toiture.
|
|
Accumulateur Ni-MH.
Un lycéen souhaite réaliser des courses miniatures avec une voiture électtrique.
BUGGY : radiocommandé, moteur électrique de puissance 40 W, vitesse mxi 45 km / h ; masse 1410 g.
Chargeur automatique : il fonctionne sous 230 V en délivrant un courant de 1 A. Soit 2 h de charge pour un accumulateur de 2000 mAh.
Accumulateur Ni-MH 7,2 V, 2200 mAh.
La télécommande fonctionne avec 4 piles AA et communique à distance à une fréquence de 2,4 GHz.
1. Le vendeur
fournit un accumulateur pour l'alimentation de la voiture et recommande
l'achat de piles pour la télécommande. Quelle est la principale
différence entre pile et accumulateur ? Pourquoi le vendeur
privilégie-t-il l'une ou l'autre technologie selon l'usage.
Une pile, une fois usée, ne se recharge pas.
Un accumulateur peut être rechargé plusieurs dizaines, voir quelques centaines de fois.
Le moteur électrique de la voiture consomme beaucoup d'énergie ( d'où
le choix d'un accumulateur) ; la télécommande consomme peu d'énergie (
d'où le choix des piles).
2. Déterminer la quantité d'électricité Q disponible dans l'accumulateur Ni-MH.
Q = 2,2 Ah = 2,2 x3600 =7 920 C.
3. Calculer l'énergie disponible Eélec que peut fournir l'accumulateur.
Eélec = Q U = 7920 x7,2 =5,7 104 J.
4. Identifier la puissance électrique moyenne Pélec absorbée par la voiture. En déduire la durée maximale possible du jeu sans recharge de l'accumulateur.
Pélec = 40 W ; durée = Eélec / Pélec =5,7 104 / 40 =1425 s ~24 minutes.
Les deux demi-équations aux électrodes lors de la recharge de l'accumulateur sont :
M(s) +H2O(l) +e- --> MH(s) +HO-aq.
Ni(OH)2(s) +HO-aq --> NiOOH(s) +H2O(l) +e- .
5. Quels sont les deux couples oxydant / réducteur ( écrit sous la forme Ox / Red ) mis en jeu au cours de la recharge ?
NiOOH(s) / Ni(OH)2(s) et M(s) / MH(s).
6. Identifier la demi-équation correspondant à une réduction. Justifier.
Un oxydant se réduit en gagnant un ou plusieurs électrons.
M(s) +H2O(l) +e- --> MH(s) +HO-aq.
7. Etablir l'équation globale de fonctionnement en charge de cet accumulateur.
M(s) +Ni(OH)2(s) --> MH(s) +NiOOH(s).
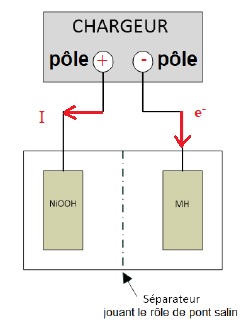
8. Compléter le
schéma en précisant le sens du courant, le sens de déplacement des
électrons lors de la charge, la polarité du chargeur.
9. Le lycéen
envisage d'effectuer des courses de vitesse avec son véhycule. Il
hésite entre deux modèles d'accumulateurs. Justifier le choix le plus
judicieux pour alimenter l'accumulateur.
A pleine vitesse, l'accumulateur se décharge rapidement. Il faut donc un grand nombre de cycle charge / décharge.
De plus pas de risque d'explosion de l'accumulateur sans système de protection.
Accumulateur Ni-MH : nombre de cycle charge / décharge : 800 à 1000.
|
|

