Mathématiques,
bac St2S Nlle Calédonie 12 / 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Exercice 1. 6 points.
Ces dernières années, la rougeole a fait son retour suite à la diminution du nombre de personnes vaccinées.
Dans une région française, une étude statistique a montré que :
- 79 % de la population est vaccinée contre la rougeole ;
- parmi ces personnes vaccinées, 0,1 % ont contracté cette maladie ;
- parmi les personnes non vaccinéescontre la rougeole, 10 % ont cotracté cette maladie.
On choisit au hasard une personne concernée par cette enquète. Chaque personne a la même probabilité d'être choisie.
On considère les événements suivants :
R : la personne est atteinte de la rougeole.
V : la personne est vaccinée contre la rougeole.
1.a. Calculer P(V).
P(V) = 0,79.
1.b. Calculer PV(R) + Pnon V(R).
PV(R) = 0,1 /100 = 0,001 ; Pnon V(R) = 10 /100 = 0,10 ; PV(R) + Pnon V(R)= 0,101.
2. Compléter l'arbre pondéré ci-dessous :
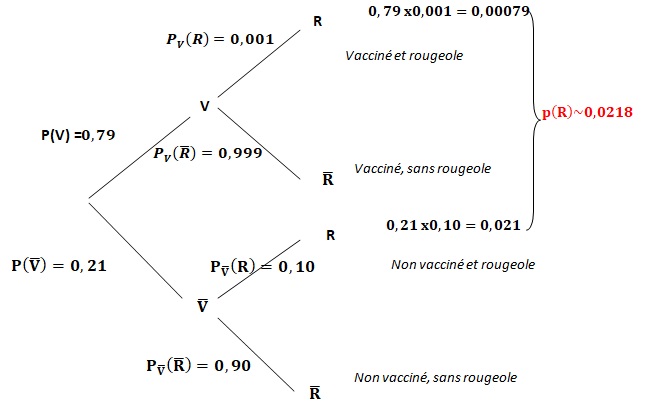
3. Décrire par une phrase l'événement non V n R.
La personne n'est pas vacciné et elle attrape la rougeole.
P(non V n R) =0,10 x 0,21 = 0,021.
4. Démontrer que la probabilité de l'événement R est égale à 0,0218.
Formule des probabilités totales : PV(R) + Pnon V(R) = 0,00079 +0,021 ~0,0218
5. La personne choisie est atteinte de la rougeole. Calculer la probabilité qu'elle ne soit pas vaccinée.
PR non V =P(R n non V) / P(R) =0,021 / 0,0218 ~0,9633.
6.
La région compte 2 millions d'habitants. Un journal affirme "
recrudescence des cas de rougeole : plus de 40 000 malades dans la
région". Cette affirmation est-elle correcte ?
0,0218 x 2 000 000 =43600. L'affirmation est correcte.
Exercice 2. 6 points.
A. Evolution du nombre de trotinettes électriques vendues en France.
On considère la fonction f définie sur [0 ; 10 ] par f(x) = 100 000 x 2,29x.
1. Quel est le sens de variation de la fonction f ? Justifier.
2,29 > 1 : la fonction 2,29x est strictement croissante sur [0 ; 10} ; il en est de même de la fonction f(x).
2. Pour tout entier naturel n <
10, on admet que le nombre de trotinettes électriques vendues en France
au cours de l'année 2014 +n est la valeur de f(n) arrondie à l'unité.
a. Calculer le nombre de trotinettes électriques vendues en 2015.
f(1) = 100 000 x2,29 = 229 000.
b. Déterminer l'année au cours de laquelle le nombre de trotinettes électriques vendues en France dépassera le million.
100 000 x 2,29n > 1 000 000 ; 2,29n > 10 ; n ln(2,29) > ln 10 ; n > ln(10) / ln(2,29) ; n >2,78 ; n = 3 (année 2017).
B. Evolution du prix des trotinettes électriques en fonction du temps.
Année
|
2015
|
2016
|
2017
|
2018
|
2019
|
rang de l'année xi
|
1
|
2
|
3
|
4
|
5
|
prix moyen en euro yi
|
870
|
767
|
618
|
477
|
399
|
1 Déterminer les coordonnées du point moyen G du nuage de points et le placer dans le repère
xG =(1+2+3+4+5) /5 = 3.
yG=(870+767+618+477+399) / 5 =626,2.
2. On décide d'ajuster ce nuage de points par la droite D d'équation y = -123,2 x+995,8.
On admet que cet ajustement reste valable jusqu'en 2022.
a. Démontrer que G appartient à cette droite.
-123,2 * 3 +995,8 =626,2 = yG.
b. Tracer la droite D en indiquant les points utilisés.
Point G et point de coordonnées (0 ; 995,8).
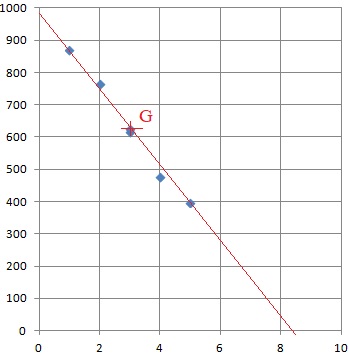
3. Calculer le prix moyen d'une trotinette en 2020.
x = 6 ; y = -123,2 *6 +995,8 =256,6 €.
4. Déterminer, selon ce modèle, l'année au cours de laquelle le prix moyen d'une trotinette sera inférieur à 130 €.
-123,2 x+995,8 < 130 ; -123,2 x < 130-995,8 ; 123,2 x >865,8 ; x > 865,8 / 123,2 ; x >7,028.
On retient x > 8 ( année 2022).
|
...
|
....
|
Exercice 3. 8 points.
Partie A.
En
1985, la population de France métropolitaine était de 55 284 000
habitants. Cette population a augmenté de 0,51 % par an jusqu'en 2020.
1. Calculer le nombre d'habitant en 1986.
55 284 000 *(1+0,51 /100)= 55 565 949.
2. On modélise le nombre d'habitants par une suite (un) de premier terme u0 =55 284 000 ; un représente le nombre d'habitants en 1985 +n.
a. Quelle est la nature de la suite (un) ? Préciser sa raison.
Suite géométrique de raison 1,0051.
b. Exprimer un en fonction de n.
un = u0 x1,0051n =55 284 000 x1,0051n.
c. Estimer au millier près, le nombre d'habitants en 2020.
n =35 ; u35 =55 284 000 x1,005135 ~66 057 800.
B. Second modèle.
On modélise la population par la fonction f définie sur [0 ; 40] par f(x) = -0,0003 x3+0,0117x2+0,1728x+55,2.
f(x) est exprimé en million d'habitants et x est le nombre d'années à partir de 1985.
1. Calculer f '(x).
f '(x) =-0,0003 *3 x2 +0,0117*2x +0,1728.
f '(x) = -0,0009x2 +0,0234x+0,1728.
2. Démontrer que f '(x) = 0,0009(32-x)(x+6).
0,0009(32-x)(x+6) =0,0009(32x+192-x2-6x) =0,0009(26x+192-x2) = -0,0009x2 +0,0234x+0,1728.
b. Compléter le tableau de signe et en déduire le tableau de variation de f(x).
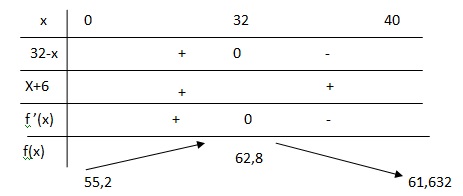
4. Quel est le maximum de la population et en quelle année est-il atteint ?
62,8 millions en 2017.
C. En 2019 la
population de France métropolitaine était d'environ 65 millions
d'habitants. Lequel de ces deux modèles semble le plus adapté ?
Premier modèle : 65,7 millions.
Second modèle : 62 millions.
Le premier modèle semble le plus adapté.
|
|