Mathématiques,
nombres complexes et géométrie, suites, bac 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Le plan complexe est muni d'un repère
orthonormé direct.
On considère la suite de nombres complexes (zn) définie par :
z0 =0 et pour tout entier n, zn+1=(1+i)zn-i.
On note An le point d'affixe zn. On note B le
point d'affixe 1.
1.a. Montrer que z1
= -i et que z2 = 1-2i.
z1=(1+i)z0-i
= -i.
z2=(1+i)z1-i
= =-(1+i)i-i =-2i-i2=1-2i.
b. Calculer z3.
z3=(1+i)z2-i
= =(1+i)(1-2i)-i =1-2i+i-2i2-i=
3-2i.
c. Placer les
points B, A1, A2 et A3.
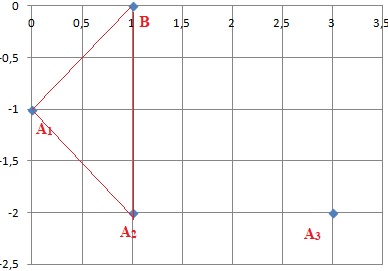
d. Démontrer que le
triangle BA1A2 est rectangle isocèle.
A1B2=12+12=2.
A1A22=12+(-2-(-1))2=2.
A1B=A1A2 : le triangle BA1A2 est isocèle.
A2B2=(1-1)2+(-2-0)2=22=
A1B2
+A1A22.
D'après la réciproque du théorème de Pythagore, le triangle BA1A2
est rectangle est A1.
2. Pour tout entier
naturel n, on pose un = |zn-1|.
a. Démontrer que un+1
= 2½un.
|zn+1-1|=|(1+i)zn-i-1|=
|(1+i)zn-(i+1)|=|(1+i)
(zn-1)|.
|zn+1-1|=(12+12)½ |zn-1| =2½|zn-1| ; un+1 = 2½un.
b. Déterminer à
partir de quel entier naturel n, la distance BAn est
strictement supérieure à 1000.
BAn
=|zn-1| =un.
La suite (un) est géométrique de raison 2½ et de
premier terme u0 =|0-1| =1.
un = (2½)n > 1000 ; n ln(2½) > 1000 ; 0,5n ln(2) > ln(1000 );
n > 2 ln(1000) / ln(2) ; n >20.
3. a. Déterminer la
forme exponentielle du nombre complexe z=1+i.
Module de z : |z| = (12+12)½ = 2 ½.
z / |z| = 1 / 2 ½+
i/ 2 ½ = cos (p/4) + i sin (p /4).
z = 2½exp(ip/4).
b. Démontrer par
récurence que pour tout entier naturel zn = 1-20,5n
exp(i n p/4).
Initialisation
: z0 = 0= 1-20 exp(0)1-1=0.
La propriété est vraie au rang zéro.
Hérédité :
la propriété est supposée vraie au rang n.
zn = 1-20,5n
exp(i n p/4).
zn+1=(1+i)zn-i.
1+i =2½exp(ip/4) ;
zn+1=2½exp(ip/4) [1-20,5n exp(i n p/4)] -i.
zn+1=2½exp(ip/4) -20,5(n+1) exp(i (n+1) p/4)] -i.
zn+1=1+i
-20,5(n+1)
exp(i (n+1) p/4)] -i.
zn+1=1
-20,5(n+1)
exp(i (n+1) p/4)].
La propriété est vraie au rang n+1.
Conclusion
: la propriété est vraie au rang zéro et héréditaire ; elle est vraie
pour tout entier n.
c. Le point A2020
appartient-il à l'axe des abscisses ? Justifier.
z2020 =
1-21010 exp(i 505 p).
505 p = 252 x 2p+p.
z2020 =
1-21010 exp(i
p) =
1+21010, nombre réel.
Le point A2020
appartient à l'axe des abscisses.
|