Mathématiques, géométrie dans l'espace, bac Polynésie 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Dans l’espace, on considère le cube ABCDEFGH d’arête de longueur égale à 1. On munit l’espace du repère orthonormé. 1. Par lecture graphique, donner les coordonnées des points B, D, E, G et H. B( 1 ; 0 ; 0). D(0 ; 1 ; 0). E(0 ; 0 ; 1). G(1 ; 1 ; 1). H(0 ; 1 ; 1). 2.a. Quelle est la nature du triangle EGD ? Justifier la réponse. EG = GD = ED =2½ ( diagonale d'un carré de côté 1 ). Le triangle EGD est équilatéral. b. On admet que l’aire d’un triangle équilatéral de côté c est égale à √3/4c2. Montrer que l’aire du triangle EGD est égale à √3 /2. c = √2 ; aire du triangle EGD =√3/4 x2 = √3 /2. 3. Démontrer que les coordonnées de M sont (2/3 ;1/3 ;1/3). 4.a. Justifier que le vecteur 𝑛⃗ (−1 ;1 ;1) est normal au plan (EGD). b. En déduire qu’une équation cartésienne du plan (EGD) est : −𝑥+𝑦+𝑧−1=0. Equation cartésienne de ce plan : -x+y+z+d=0. E(0 ; 0 ; 1) appartient à ce plan :0 +0 +1 +d = 0 ; d = -1. c. Soit 𝒟 la droite orthogonale au plan (EGD) et passant par le point M. Montrer qu’une représentation paramétrique de cette droite est : 𝒟:{ 𝑥=2/3−𝑡 ; 𝑦=1/3+𝑡 ; 𝑧=1/3+𝑡, 𝑡 ∈ 𝐑. 𝑛⃗ (−1 ;1 ;1) est un vecteur directeur de cette droite et M appartient à cette droite : x = xM-t =2 / 3 -t. y = yM+t = 1 / 3 +t. z = zM+t = 1 / 3 +t avec t réel. ... .... 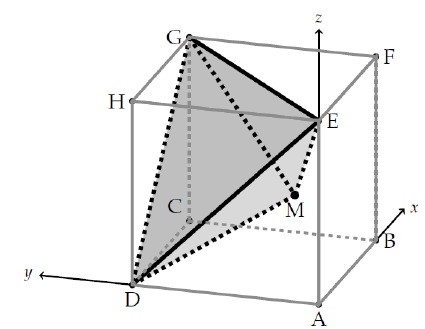5. Le cube ABCDEFGH est représenté ci-dessus selon une vue qui permet de mieux percevoir la pyramide GEDM, en gris sur la figure : Le but de cette question est de calculer le volume de la pyramide GEDM. a. Soit K, le pied de la hauteur de la pyramide GEDM issue du point M. Démontrer que les coordonnées du point K sont (1/3 ;2/3 ;2/3). K(x  ; y  ; z). K appartient au plan GDE : -x+y +z-1=0. K appartient à la droite D : x =2 / 3 -t. y =  1 / 3 +t. z =  1 / 3 +t avec t réel. -2 / 3+t +1 / 3+t +1 / 3 +t -1=0.  -1+3t=0. t = 1 /3. x=2 /3 -1 /3 = 1 /3. y =1 /3 +1 /3 = 2 /3. z = 1 /3 +1/3 = 2 /3. b. En déduire le volume de la pyramide GEDM. V= aire de base x hauteur /3. V = aire du triangle GDE x KM /3. Aire du triangle GDE =√3 /2. KM2=(2/3-1/3)2+(1/3-2/3)2+(1/3-2/3)2=1/3. KM = 1 /√3 . V = √3 /2 x 1 /√3  / 3 = 1 /6.

menu