Mathématiques,
suite, probabilités, bac Polynésie 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
Suites.
On considère la suite (un) définie par u0 = 10 000 et pour tout entier n par un+1 =0,95 un +200.
1. Calculer u1 et vérifier que u2 = 9415.
u1 = 10 000 x0,95 +200 =9700.
u2 = 9700 x0,95 +200 =9415.
2.a Démontrer par récurrence que un > 4000.
Initialisation : u0 = 10 000 , la propriété est vraie au rang zéro.
Hérédité : la propriété est supposée vraie au rang n : un > 4000.
Démontrons qu'elle est vraie au rang n+1.
un+1 =0,95 un +200.
un+1 >0,95 x 4000 +200.
un+1 > 4000.
La propriété est donc vraie au rang n+1.
Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est vraie pour tout entier naturel n.
2.b. On admet que la suite est décroissante. Justifier qu'elle converge.
La suite est décroissante et minorée par 4000, donc elle converge.
3. On considère la suite (vn) définie par vn = un-4000.
3.a. Calculer v0.
v0 = u0-4000 = 6000.
3.b. Démontrer que (vn) est une suite géométrique.
vn+1 = un+1-4000.
vn+1 =0,95 un +200 -4000.
vn+1 =0,95 un -3800.
vn+1 =0,95( un -4000)
vn+1 =0,95 vn.
(vn) est une suite géométrique de raison 0,95 et de premier terme 6000.
3.c En déduire que un = 4000 + 6000 x0,95n.
vn = 6000 x0,95n = un-4000.
un= 4000 + 6000 x0,95n.
3.d. Quelle est la limite de la suite (un) ?
-1 < 0,95 < 1 , 0,95n tend vers zéro quand n tend vers plus l'infini.
un tend vers 4000 si n tend vers plus l'infini.
4. En
2020 une espèce animale comptait 10 000 individus. l'évolution observée
les années précédentes conduit à estimer qu'à partir de 2021 cette
population baissera de 5 % chaque début d'année. On décide d'introduire
200 individus à la fin de chaque année, à partir de 2021.
Un responsable affirme " l'espèce ne devrait pas s'éteindre, mais nous
n'empêcherons pas une disparition de plus de la moitié de la
population".
Que pensez de cette affirmation ? Justifier.
Population initiale : 10 000.
Population au bout d'un temps très long : 4000, valeur inférieure à 5000.
L'affirmation est donc vraie.
|
...
|
....
|
Probabilités.
Un test est mis au point pour détecter une maladie dans un pays.
Selon les autorités sanitaires de ce pays, 7 % des habitants sont infectés par cette maladie.
Parmi les individus infectés, 20 % sont déclarés négatifs.
Parmi les individus sains, 1 % sont déclarés positifs.
Une personne est choisie au hasard dans la population.
On note :
M l’évènement : « la personne est infectée par la maladie » ;
T l’évènement : « le test est positif ».
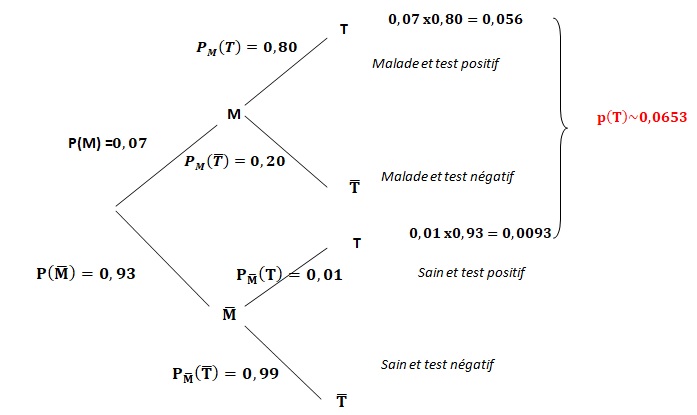
1. Construire un arbre pondéré modélisant la situation proposée.
2. a. Quelle est la probabilité pour que la personne soit infectée par la maladie et que son test soit positif ?
b. Montrer que la probabilité que son test soit positif est de 0,0653.
3. On sait que le
test de la personne choisie est positif. Quelle est la probabilité
qu’elle soit infectée ? On donnera le résultat sous forme approchée à 10−2 près.
PT(M)=P(T n M) / P(T)=0,056 /0,0653 ~0,86.
4. On choisit dix
personnes au hasard dans la population. La taille de la population de
ce pays permet d’assimiler ce prélèvement à un tirage avec remise. On
note X la variable aléatoire qui comptabilise le nombre d’individus
ayant un test positif parmi les dix personnes.
a. Quelle est la loi de probabilité suivie par X ? Préciser ses paramètres.
Les tirages sont aléatoires, indépendants et identiques.
A chaque tirage, il y a deux issues : " test positif" ou "test négatif".
X suit la loi binomiale de paramètre p = 0,0653 et n = 10.
b. Déterminer la
probabilité pour qu’exactement deux personnes aient un test positif. On
donnera le résultat sous forme approchée à 10−2 près.
p(X=2) = C102 x0,06532 (1-0,0653)8=10 x9 / 2 x0,00426 x 0,583 ~0,11.
5. Déterminer le
nombre minimum de personnes à tester dans ce pays pour que la
probabilité qu’au moins une de ces personnes ait un test positif, soit
supérieure à 99 %.
P(X > 1)=1-P(X=0) > 0,99.
P(X =0)< 0,01.
Cn0 x0,06530 (1-0,0653)n <0,01.
1x1 x0,9347n < 0,01.
n ln(0,9347) < ln(0,01).
-0,06753 n < -4,605.
n > 4,605 / 0,06753.
n > 68.
|
|